
Mastering the concepts covered in this section is crucial for understanding key mathematical principles. By reviewing the key approaches and techniques, you’ll gain the confidence needed to tackle a wide range of problems. This section aims to break down complex topics into easily digestible steps, ensuring a deeper understanding.
Step-by-step guides will help clarify the processes involved, enabling you to work through each problem with precision. By practicing regularly and focusing on common pitfalls, you can refine your skills and improve your performance.
Additionally, we will explore effective strategies for preparing efficiently, with practical exercises and expert tips to ensure mastery of the material. Whether you’re working independently or reviewing for assessments, this guide will provide the structure needed to succeed.
Mathematical Problem Solutions: Key Concepts

This section provides a comprehensive approach to solving mathematical problems presented in this specific area of study. It covers essential techniques and logical steps necessary to understand and navigate through different types of exercises. By applying these methods, you can solve a variety of challenges with ease and confidence.
Breaking Down Complex Problems

Understanding the underlying principles is crucial for success. We will explore methods that simplify intricate calculations and reasoning, making even the most difficult questions easier to approach. Focus is placed on breaking down problems into manageable parts, allowing for efficient solutions.
Practical Application and Mastery
Once the basics are understood, applying them in real scenarios is the next step. This section offers practical exercises that demonstrate how these principles are used in different contexts, helping solidify knowledge and prepare for any assessment or challenge.
Key Concepts of Chapter 11

This section introduces the fundamental ideas and principles that form the basis of the exercises covered. A solid understanding of these core concepts is essential for tackling more complex problems effectively. These principles will provide a structured approach to working through challenges and mastering the material.
Core Principles and Methods
Here are the key ideas to focus on:
- Understanding the relationship between different elements in mathematical contexts
- Identifying patterns and applying them to various situations
- Utilizing formulas and rules to simplify calculations
- Breaking down complex scenarios into smaller, solvable steps
Strategies for Applying Concepts
Once you grasp the fundamental principles, it’s important to practice applying them in practical exercises. These techniques can help solidify your understanding:
- Begin by solving simpler problems to build confidence
- Gradually work towards more complex scenarios as your skills improve
- Review key steps regularly to reinforce understanding
- Seek additional challenges to test your mastery
Step-by-Step Solutions to Problems
This section provides detailed solutions to help you understand the process of solving mathematical challenges. Breaking down each problem into clear, manageable steps ensures you can follow along and grasp the techniques used to reach the correct solution. By following these methods, you can improve your problem-solving skills and gain more confidence in your abilities.
How to Approach Each Problem
To tackle any problem effectively, follow these steps:
- Read the problem carefully and identify the key elements.
- Visualize the problem by drawing diagrams or setting up equations if necessary.
- Break the problem into smaller parts, addressing one aspect at a time.
- Apply the relevant rules or formulas that fit the situation.
- Double-check the calculations and ensure all conditions are met.
Example Problems and Solutions

Here are a few example problems, along with their step-by-step solutions:
- Example 1: How to solve for unknowns in basic equations.
- Example 2: Step-by-step process for calculating areas or volumes of specific shapes.
- Example 3: Analyzing word problems and setting up the correct approach.
Common Mistakes and How to Avoid Them
When working through any complex set of problems, it’s easy to fall into the trap of making small yet impactful errors. Identifying these frequent mistakes and knowing how to address them can greatly improve overall accuracy and understanding. In this section, we explore some of the most common missteps people encounter and offer practical suggestions for avoiding them.
Key Mistakes and Their Solutions
The following table highlights typical errors and how to prevent them:
| Common Mistake | How to Avoid It |
|---|---|
| Misunderstanding the problem requirements | Always read the instructions carefully and break the problem into smaller parts to ensure you understand all aspects. |
| Relying on incorrect assumptions | Verify every assumption before proceeding. Double-check the provided information and avoid jumping to conclusions. |
| Forgetting to apply necessary operations | Stay organized and track your steps to ensure all required actions are performed in the correct sequence. |
| Overcomplicating the solution | Look for the simplest approach to solve the problem. Sometimes the most straightforward solution is the correct one. |
By staying vigilant and following these tips, you can minimize the risk of making these common mistakes and approach problems with greater confidence and accuracy.
Strategies for Effective Test Preparation
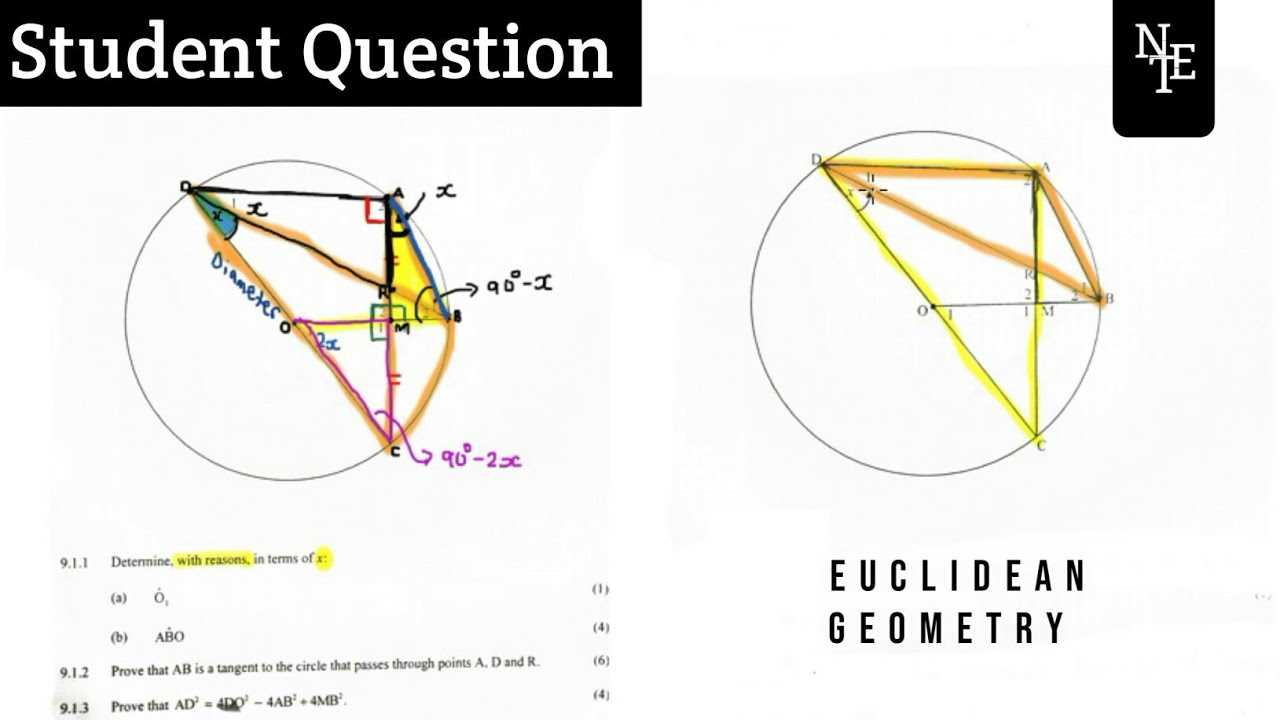
Preparing for any kind of assessment requires a structured approach that focuses on mastering key concepts and reinforcing understanding. By utilizing the right strategies, you can optimize your study sessions and improve your performance. In this section, we will explore various methods to help you prepare effectively, ensuring that you’re ready to tackle any challenge that comes your way.
Time Management and Scheduling
One of the most critical aspects of preparation is managing your time wisely. Creating a study schedule allows you to allocate sufficient time for each topic, ensuring that you don’t rush through important material. Prioritize areas that need more focus, and be sure to include breaks to avoid burnout.
Active Learning Techniques
Rather than passively reading or reviewing notes, engage with the material actively. Practice solving problems, teach the concepts to someone else, or create flashcards to test your knowledge. Active learning reinforces understanding and helps you retain information more effectively.
Practice Questions for Mastery
To truly grasp any subject, consistent practice is essential. Working through a variety of questions allows you to apply theoretical knowledge to real-life situations, testing both your understanding and problem-solving abilities. By practicing regularly, you can identify areas of weakness and reinforce your strengths. In this section, we will introduce some practice questions designed to help you master the key concepts and approaches needed to succeed.
Question 1: Solve for the unknown value in the following problem: A rectangle has a length of 8 units and a width of 5 units. What is the perimeter?
Question 2: Calculate the area of a triangle with a base of 10 units and a height of 6 units. How does this differ when the height is doubled?
Question 3: Identify the properties of a parallelogram, and use those properties to find the missing side length when given sufficient information.
Remember, the key to mastering these problems is consistent practice and a focus on understanding the underlying principles, not just memorizing formulas.
Additional Resources for Success
To enhance your understanding and mastery of essential concepts, using various resources outside of traditional lessons can be highly beneficial. These materials can provide further explanations, alternative methods, and opportunities to engage with topics more deeply. Whether you prefer online tools, textbooks, or interactive platforms, having access to diverse resources ensures you can reinforce your knowledge and overcome challenges effectively.
Explore websites offering interactive exercises and video tutorials, read specialized books that provide different perspectives on problem-solving, or join study groups where you can discuss ideas with peers. Each of these options will add valuable insights to your learning process and help you build the necessary skills for success.