
As you approach the end of your studies in this essential branch of mathematics, it’s important to reinforce your knowledge and strengthen your problem-solving abilities. The assessment tests a variety of concepts, ranging from foundational principles to more complex applications. Understanding the key components and their interconnections will help you confidently tackle any question that comes your way.
Effective preparation requires both theoretical understanding and practical experience. Focusing on critical topics and applying the learned techniques to different scenarios is key to achieving success. Through consistent practice, you’ll not only refine your skills but also gain a deeper appreciation for the subject.
To assist you in this process, this guide offers helpful resources, tips, and example questions. With focused effort, you can approach the challenge with a solid grasp of the material and a well-prepared mindset.
Key Topics to Review for Calculus 1 Exam
To ensure you are fully prepared, it’s important to focus on the most relevant concepts that will be tested. These essential topics lay the foundation for problem-solving and help you understand the underlying principles of the subject. Below are the key areas to concentrate on during your preparation.
- Limits and Continuity: Understand the behavior of functions as they approach specific points, and identify when functions are continuous or discontinuous.
- Derivatives: Review how to compute the rate of change of a function, including the power rule, product rule, quotient rule, and chain rule.
- Applications of Derivatives: Study practical applications like optimization problems and motion analysis, which rely heavily on derivative concepts.
- Integrals: Focus on the techniques of integration, such as the power rule for integrals and integration by substitution.
- Fundamental Theorem of Calculus: Make sure you understand the relationship between differentiation and integration and how to apply this theorem in various contexts.
- Sequences and Series: Familiarize yourself with the behavior of infinite sequences and series, including convergence tests and basic series expansions.
By dedicating time to each of these areas, you will ensure a deeper comprehension and be prepared for a range of problems that may appear. Practice with sample problems and apply the concepts to real-world scenarios for a more comprehensive understanding.
Practice Problems to Boost Your Skills

Practicing a variety of problems is one of the most effective ways to reinforce your understanding of key concepts. By repeatedly working through different scenarios, you’ll build confidence and improve your ability to solve challenging questions. This section will guide you through a selection of practice problems that target the most critical areas of the subject.
Essential Problem Types

Focus on the types of problems that you are most likely to encounter. These include basic computations, applied problems, and complex scenarios that require multiple techniques. The more you practice, the more intuitive these concepts will become.
- Rate of Change Problems: Calculate the rate at which one quantity changes relative to another.
- Optimization Problems: Maximize or minimize a given function by applying derivative rules.
- Area Under a Curve: Use integration to find the area between a curve and the x-axis.
Increasing Problem Difficulty

Start with simpler problems to build your skills, and then progressively tackle more difficult ones. Challenge yourself with problems that incorporate multiple concepts, as these are more representative of what you may encounter in assessments.
- Combined Techniques: Solve problems that require both differentiation and integration methods.
- Advanced Applications: Tackle real-world scenarios such as population growth or physics-based motion problems.
By working through these problems, you will not only improve your problem-solving skills but also gain a deeper understanding of the material. Consistent practice is the key to mastering any mathematical concept.
Understanding Limits and Continuity
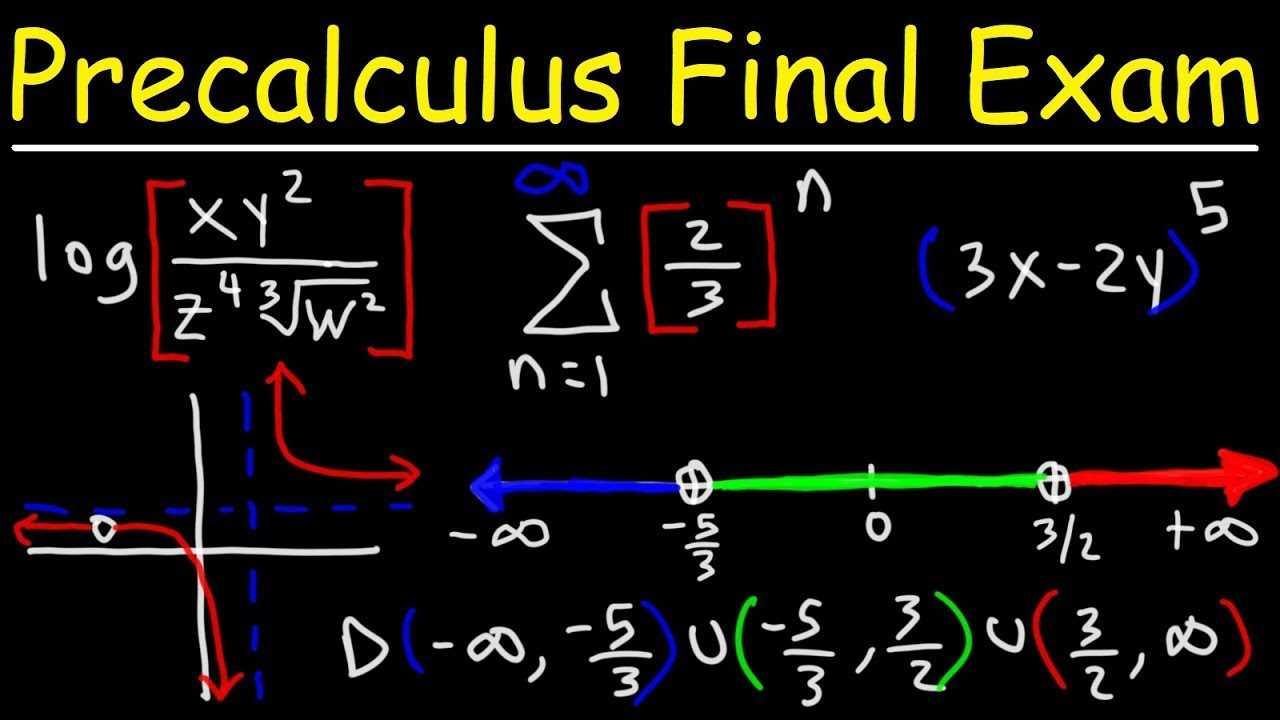
Grasping the behavior of functions near specific points is crucial for solving many problems. Limits help describe how a function behaves as it approaches a particular value, while continuity ensures that the function has no abrupt jumps or breaks. A solid understanding of these concepts will provide a foundation for more advanced topics.
Limits help us analyze the behavior of functions at boundary points, and continuity ensures smooth, uninterrupted changes. Knowing how to calculate limits and determine continuity is essential for solving real-world problems where functions may approach certain values but never quite reach them.
| Concept | Definition | Example |
|---|---|---|
| Limit | The value that a function approaches as the input approaches a given point. | As x approaches 2, the limit of f(x) = x² is 4. |
| Continuity | A function is continuous if there are no jumps, breaks, or holes in its graph. | f(x) = x³ is continuous for all real numbers. |
| Discontinuity | Occurs when a function has a break or jump in its graph. | f(x) = 1/x has a discontinuity at x = 0. |
To master these concepts, it is vital to practice finding limits of various functions and determining where they are continuous or discontinuous. The more familiar you become with these ideas, the easier it will be to tackle complex problems in the future.
Mastering Derivatives for the Exam
Becoming proficient in derivatives is essential for solving a wide variety of problems. This concept involves determining the rate of change of a function and is fundamental to understanding motion, growth, and optimization in various fields. Mastery over this topic allows you to approach complex scenarios with confidence and accuracy.
To truly master this skill, you need to be comfortable applying different rules for differentiation, such as the power rule, product rule, quotient rule, and chain rule. These techniques provide a toolkit for differentiating a broad range of functions, from simple polynomials to more intricate expressions involving products and quotients.
Focusing on recognizing the structure of a problem and selecting the appropriate rule to apply is key. Practicing various examples will help reinforce these techniques and improve speed and accuracy. With consistent practice, you will develop an intuitive grasp of how to handle derivatives in diverse contexts.
Applications of Integrals in Calculus 1
Integrals play a crucial role in solving real-world problems by providing a means to calculate areas, volumes, and other quantities that accumulate over time or space. Understanding how to apply integration methods to practical situations is essential for mastering this concept and solving complex problems effectively.
Here are some key applications of integration:
- Area under a Curve: Integrals are often used to calculate the area between a function and the x-axis, which is essential in various fields such as physics and economics.
- Volume of Solids: By using integration, you can calculate the volume of 3D objects, such as cylinders, spheres, or irregular shapes, by revolving a curve around an axis.
- Work and Energy: Integration is used to calculate work done by a force acting on an object over a distance, which is fundamental in mechanical engineering and physics.
- Average Value of a Function: It allows you to determine the average value of a function over a given interval, which has applications in statistics and data analysis.
Mastering these applications will not only help you solve theoretical problems but will also provide insights into their use in real-world scenarios, making the concept much more relevant and practical. By practicing these applications, you can strengthen your understanding and ability to solve a wide range of problems.
Final Exam Tips and Strategies

Preparing effectively for an assessment requires a combination of focused study, time management, and the ability to approach problems with a clear strategy. Knowing how to allocate your time, focus on key areas, and avoid common mistakes can significantly improve your performance.
Here are some useful tips to help you succeed:
- Review Key Concepts: Focus on the most important topics that frequently appear in assessments. Ensure that you understand core principles like differentiation, integration, and limits.
- Practice Problem Solving: Work through a variety of problems to get comfortable with different question types. This will help you develop problem-solving strategies and identify common patterns.
- Manage Your Time: During the test, pace yourself to avoid spending too much time on any one question. Prioritize easier problems first to secure quick points and revisit the harder ones later.
- Stay Calm and Confident: Anxiety can negatively affect performance. Practice relaxation techniques and remain confident in your abilities. Trust that your preparation will pay off.
By following these strategies, you can maximize your preparation and perform confidently, knowing that you have taken the right steps to succeed in the assessment. Time and practice are key to mastering the material and boosting your performance when it matters most.