
Understanding the fundamental principles of mathematics is crucial for building a strong foundation. The initial lessons often cover essential theories and techniques that serve as stepping stones to more complex topics. By focusing on core elements, students can ensure a deeper comprehension that will benefit them in future studies.
Having a clear grasp of basic concepts helps avoid confusion when encountering more advanced material. Proper practice and reviewing the right materials are vital to reinforcing these ideas. This section provides a comprehensive guide to tackling the first set of challenges, with insights that make the process easier and more effective.
In this article, we will discuss strategies to confidently approach common questions and refine your problem-solving skills. Whether you’re revisiting these ideas or preparing for upcoming assessments, the following information will help you progress with ease.
Understanding Foundational Concepts for Success

The first step in mastering any mathematical discipline is to become familiar with the essential ideas that form the groundwork. These fundamental principles are critical for progressing in more advanced topics and ensuring that later lessons are approached with confidence. Grasping the core concepts early on helps you build a strong foundation for future learning.
Basic shapes, measurements, and relationships are some of the key elements that are introduced at the beginning. These concepts create the building blocks for more complex theories that will be explored in later stages. Understanding how different figures interact with each other, how to measure their properties, and how to apply these measurements to solve problems is crucial to your development.
Focusing on practice exercises and reviewing basic formulas will help solidify your understanding and improve your ability to apply these ideas effectively. The more you familiarize yourself with the key concepts, the easier it will be to tackle the more challenging problems ahead. The foundation you build here will directly influence your success as you advance in your studies.
Key Concepts Covered in Initial Evaluation
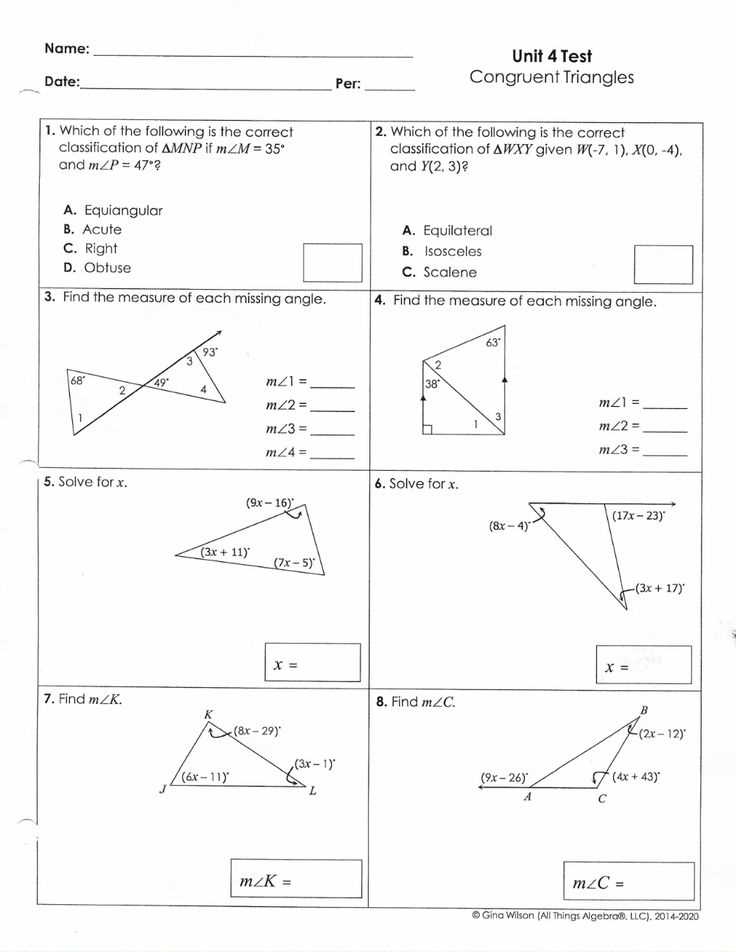
In this section, we explore the essential principles that are typically assessed in the first evaluation of mathematical skills. These concepts are fundamental and serve as the foundation for more complex problem-solving tasks. Understanding these key areas will significantly improve your ability to perform well in subsequent challenges.
Shapes and Their Properties
One of the primary focuses in the early stages is understanding various shapes and their defining characteristics. Some important aspects include:
- Identifying different polygons such as triangles, squares, and rectangles
- Understanding the properties of circles and other curves
- Calculating perimeter, area, and other relevant measurements
Basic Measurement Techniques
Another crucial aspect covered involves measurement skills. This area typically includes:
- Working with different units of measurement (e.g., inches, centimeters, etc.)
- Converting between units and understanding scale
- Using rulers and other tools for accurate measurement
Familiarity with these concepts is key to progressing to more complex topics, where these principles will be applied in various ways to solve advanced problems. Understanding these foundational elements will provide you with the necessary skills for future success.
Step-by-Step Guide to Answering Questions

Approaching problems methodically is essential for success. By breaking down each question into manageable parts, you can ensure that you tackle it with clarity and confidence. This structured approach helps minimize errors and ensures that each aspect of the problem is carefully considered.
Follow these steps to effectively solve challenges:
- Read the problem carefully: Understand what is being asked and identify key information.
- Identify relevant concepts: Determine which principles or formulas apply to the problem.
- Draw diagrams: Visualize the problem by sketching it out to better understand relationships.
- Perform calculations: Apply the appropriate operations and check each step for accuracy.
- Review your solution: Double-check your work to ensure all steps are correct and complete.
By following this method, you can approach each question systematically and avoid overlooking critical details. This process will help you build confidence in your problem-solving abilities and improve your performance overall.
Tips for Mastering Mathematical Fundamentals
To excel in foundational mathematics, it is essential to not only understand the core concepts but also to practice and refine your skills regularly. Mastery of these elements provides the confidence to solve complex problems efficiently and accurately. The following tips will help you enhance your understanding and improve your problem-solving abilities.
Practice consistently: Regular practice is key to reinforcing what you’ve learned. Working through problems consistently will help you retain information and increase your familiarity with common patterns.
Focus on understanding, not memorization: Aim to understand the underlying principles rather than memorizing formulas. This will allow you to apply knowledge more effectively in different situations.
Use visual aids: Drawing diagrams or visualizing problems can significantly improve your ability to comprehend relationships between shapes and measurements. This approach will often make abstract concepts easier to grasp.
Review mistakes: Every mistake offers an opportunity to learn. Take time to analyze your errors and understand why they occurred. This will help you avoid similar pitfalls in the future.
By incorporating these strategies into your study routine, you’ll develop a stronger grasp of the material and improve your overall performance. Mastery of the fundamental concepts is crucial for advancing in any mathematical discipline.
Common Mistakes in Mathematical Evaluations

Even with a strong understanding of the material, it’s easy to make mistakes when solving problems. These errors often stem from overlooking details, misinterpreting questions, or applying concepts incorrectly. Recognizing these common pitfalls will help you avoid them and improve your accuracy during assessments.
Misunderstanding Problem Requirements
One frequent issue is failing to fully grasp the question. It’s essential to carefully read and understand what is being asked before attempting to solve it. Common mistakes include:
- Misinterpreting the given information
- Overlooking important details such as specific units or conditions
- Rushing through the problem without considering all aspects
Incorrect Application of Formulas
Another common mistake is using the wrong formula or applying it incorrectly. While formulas are crucial in problem-solving, improper use can lead to errors. To avoid this:
- Ensure you are using the appropriate formula for the situation
- Double-check your calculations after applying the formula
- Review the steps in the solution process to verify accuracy
By being mindful of these common errors, you can significantly improve your ability to solve problems accurately and efficiently. Recognizing and correcting mistakes early on is essential for mastering the subject matter.
How to Improve Your Test Scores
Achieving higher scores on assessments requires a combination of focused practice, effective strategies, and consistent review. By refining your approach and understanding the best methods for preparing, you can significantly enhance your performance. The following tips will guide you toward improving your results and mastering the subject matter.
Here are some key areas to focus on for better preparation:
| Strategy | Explanation |
|---|---|
| Practice Regularly | Consistent practice with exercises and problems helps reinforce knowledge and improves retention. |
| Review Mistakes | Analyze errors and understand why they occurred. This will prevent similar mistakes in the future. |
| Use Study Aids | Leverage diagrams, online resources, and study guides to supplement your learning. |
| Time Management | Practice solving problems under time constraints to build efficiency and reduce stress during the exam. |
By incorporating these strategies into your study routine, you’ll be better equipped to perform well on future assessments. Remember, consistent effort and a structured approach are key to making continuous improvements and achieving higher scores.