
In the study of mathematics, solving systems of equations is a fundamental concept. The ability to solve multiple equations with multiple unknowns allows us to find solutions to complex problems in various fields, such as physics, engineering, and economics. In this article, we will discuss the answer key for the Unit Systems of Equations Homework 1, which focuses on solving systems of equations using different methods.
The Unit Systems of Equations Homework 1 is designed to test students’ understanding of solving systems of equations through substitution, elimination, and graphing methods. This homework includes a variety of problems, ranging from simple linear equations to more complex systems involving quadratic or exponential equations. By solving these problems, students can strengthen their knowledge and skills in solving systems of equations and enhance their problem-solving abilities.
This answer key will provide step-by-step solutions to each problem in the homework, along with explanations and calculations required to arrive at the correct answer. It will serve as a valuable resource for students to check their work and understand the process of solving systems of equations. Additionally, this answer key will help teachers assess students’ understanding of the topic and provide guidance for further instruction and support.
Overall, the Unit Systems of Equations Homework 1 Answer Key serves as a comprehensive guide to solving systems of equations. Whether you are a student looking to check your work or a teacher seeking a resource to facilitate learning, this answer key will provide the necessary support and guidance to master the topic of systems of equations. Let’s explore the answer key and enhance our problem-solving skills!
Unit Systems of Equations Homework 1 Answer Key
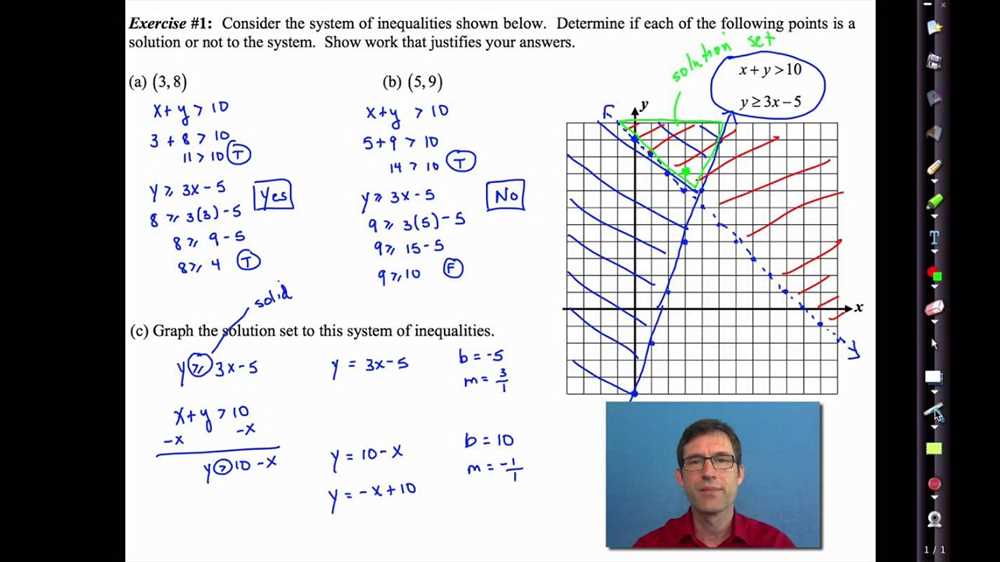
Below is the answer key for Homework 1 on unit systems of equations. This assignment focuses on solving systems of equations using different unit systems.
Problem 1:
Convert the following equations from the metric unit system to the imperial unit system:
- Equation 1: 3x + 2y = 10
- Equation 2: 2x – 5y = -8
Answer:
To convert Equation 1, we need to convert the coefficients and constant term to the imperial unit system. We multiply the metric coefficients by the conversion factor for each unit:
- 3x + 2y = 10
- 3x + 2y = 10 * 0.3048
- 3x + 2y = 3.048x + 6.096y = 10 * 0.3048
Similarly, for Equation 2, we have:
- 2x – 5y = -8
- 2x – 5y = -8 * 0.3048
- 2x – 5y = 0.6096x – 1.524y = -8 * 0.3048
Problem 2:
Solve the following system of equations:
- Equation 1: 2x + 3y = 10
- Equation 2: 4x – 5y = -8
Answer:
To solve this system of equations, we can use the method of substitution or elimination. Let’s use the elimination method:
- Multiply Equation 1 by 2 and Equation 2 by 4 to cancel out the x terms:
- 4x + 6y = 20
- 8x – 10y = -16
Next, subtract Equation 2 from Equation 1 to eliminate the y terms:
- (4x + 6y) – (8x – 10y) = 20 – (-16)
- -4x + 16y = 36
Divide both sides of the resulting equation by -4 to solve for y:
- 16y = -36
- y = -36 / 16
- y = -2.25
Substitute the value of y back into Equation 1 to solve for x:
- 2x + 3(-2.25) = 10
- 2x – 6.75 = 10
- 2x = 10 + 6.75
- 2x = 16.75
- x = 16.75 / 2
- x = 8.375
Therefore, the solution to the given system of equations is x = 8.375 and y = -2.25.
Understanding Unit Systems
When solving problems or equations in physics, it is crucial to have a good understanding of unit systems. Unit systems provide a standardized way of measuring and quantifying physical quantities. Without consistent units, it would be difficult to compare and communicate the results of scientific experiments and calculations. The International System of Units (SI) is the most widely used unit system internationally and provides a consistent framework for expressing physical quantities.
SI units consist of seven base units: meter (m) for length, kilogram (kg) for mass, second (s) for time, ampere (A) for electric current, kelvin (K) for temperature, mole (mol) for amount of substance, and candela (cd) for luminous intensity. These base units can be combined to form derived units, such as velocity (m/s) or force (kg·m/s^2).
It is essential to ensure that units are properly treated in mathematical equations. When performing calculations or solving equations, it is important to keep track of the units of each quantity to ensure that they are consistent. The use of dimensional analysis can help identify and correct any unit errors that may arise during calculations.
For example, if we are solving a problem that involves calculating the speed of a car, and the given data includes the distance traveled in meters and the time in seconds, we need to ensure that our final answer is in the correct unit, such as meters per second (m/s).
Understanding and utilizing unit systems is an essential skill in physics and other scientific disciplines. It allows for accurate and consistent measurements, calculations, and communication of findings. By carefully considering units in equations and calculations, scientists can ensure the validity and reliability of their results.
Solving Unit Systems of Equations
In mathematics, a unit system of equations refers to a set of equations where each variable represents a specific unit or quantity. These types of systems are commonly used in physics, engineering, and other scientific fields where measurements and conversions between units are necessary.
To solve a unit system of equations, it is important to first identify the variables and their corresponding units. This can be done by carefully reading the problem statement and understanding the context in which the equations are given.
Once the variables and units are identified, the next step is to set up and solve the equations using appropriate conversion factors and mathematical operations. It is crucial to ensure that the units are consistent throughout the calculations to avoid any errors or inaccuracies.
One approach to solving unit systems of equations is to use substitution. This involves solving one equation for a variable in terms of the other variables and then substituting this expression into the other equations. By repeatedly substituting and simplifying, the values of the variables can be determined.
Another approach is to use elimination, which involves adding or subtracting equations in order to eliminate one variable at a time. This method can be useful when the equations are linear and have coefficients that can be easily manipulated.
Once the values of the variables are determined, it is important to check their units to ensure that they are consistent and make sense in the given context. It is also advisable to perform any necessary unit conversions to obtain the final answers in the desired units.
In summary, solving unit systems of equations requires identifying the variables and their units, setting up and solving the equations using appropriate conversion factors and mathematical operations, and checking the units of the final answers for consistency. By carefully following these steps, accurate and meaningful solutions can be obtained.
Unit Conversion Factors
When working with different units of measurement, it is often necessary to convert between them. This is where unit conversion factors come in. These factors allow us to change the unit of a given quantity without changing its value.
Unit conversion factors are typically ratios that relate one unit to another. They are derived from the definitions and relationships between different units. For example, the conversion factor between inches and centimeters is 2.54 cm/inch, because there are 2.54 centimeters in one inch. By multiplying a measurement in inches by this conversion factor, we can obtain the equivalent measurement in centimeters.
It is important to note that unit conversion factors can be used to convert not only between different units of the same quantity, but also between different quantities. For example, the conversion factor between kilometers and miles can be used to convert a distance measurement to its equivalent in a different unit of measurement.
Unit conversion factors are a fundamental tool in fields such as science, engineering, and mathematics. They allow us to work with different units of measurement and ensure consistency and accuracy in our calculations. By understanding and using unit conversion factors correctly, we can easily convert between different units and solve problems that involve multiple units of measurement.
Importance of Unit Consistency

In any field or discipline that involves measurements and calculations, unit consistency is of utmost importance. Unit consistency refers to using the same units throughout a calculation or equation. When units are not consistent, it can lead to errors, inaccuracies, and confusion.
One of the main reasons why unit consistency is important is that it ensures the accuracy and reliability of calculations. When different units are used within the same calculation, it becomes difficult to make meaningful comparisons or draw valid conclusions. By using consistent units, the results are more reliable and can be easily understood and interpreted.
For example: Consider a problem where the distance is given in kilometers and the time is given in hours. If we want to calculate the speed in meters per second, it is essential to convert the distance and time to the appropriate units before performing the calculation. If we do not do this, the result will be in incorrect units and may not make sense.
Unit consistency is also crucial for communication and collaboration between different individuals or teams working on a project. Using consistent units allows for clear and effective communication of ideas, data, and results. It enables others to understand and reproduce the calculations or experiments, which is essential for scientific research and engineering projects.
For example: If a research paper provides measurement data in inconsistent units, it becomes challenging for other researchers to replicate the study or compare the results. This hampers the progress of science and slows down the advancement of knowledge.
In conclusion, maintaining unit consistency is vital to ensure accurate calculations, reliable results, and effective communication in any field that involves measurements and calculations. It helps to eliminate errors, confusion, and facilitates the proper interpretation and understanding of data and outcomes.
Tips for Solving Unit Systems of Equations
When it comes to solving unit systems of equations, there are a few helpful tips that can make the process easier and more efficient. Here are some key strategies to keep in mind:
1. Identify the variables:
Start by identifying the variables in the system of equations. This will help you understand the relationship between different quantities and determine the unknowns you need to solve for.
2. Choose an equation to start with:
Choose one equation from the system to start with. It is often helpful to pick the equation with the simplest coefficients or the one that looks the easiest to solve. This will make the initial steps more straightforward.
3. Solve for one variable:
Using the chosen equation, solve for one of the variables in terms of the other(s). This will help you eliminate that variable from the other equations, reducing the system to a simpler form.
4. Substitute into the other equations:
Take the expression you found for the variable and substitute it into the other equations in the system. This will help you eliminate that variable and create a new equation with fewer unknowns.
5. Repeat and simplify:
Continue solving for variables and substituting into other equations until you have a simpler system of equations with only one unknown. Then, solve for this remaining variable.
- 6. Check your solution:
Always check your solution by substituting the values back into the original system of equations. This will verify that your solution is correct and satisfies all the given equations.
By following these tips, you can successfully solve unit systems of equations and find the values of the variables in the system.
Common Mistakes in Unit Systems Homework
When working on unit systems homework, it is common for students to make certain mistakes that can affect their final answers. These mistakes often stem from a lack of understanding of the unit conversion process or a failure to apply the correct conversion factors. Here are some common mistakes to watch out for:
- Forgetting to convert units: One of the most common mistakes is forgetting to convert units when performing calculations. This can result in incorrect answers and can lead to confusion when interpreting the final results.
- Mixing up conversion factors: Another mistake is mixing up conversion factors or using the wrong ones. It is important to carefully select the appropriate conversion factors that relate the given units to the desired units. Using incorrect conversion factors can lead to incorrect final answers.
- Not recognizing and canceling units: When performing unit conversions, it is important to recognize which units cancel out and which ones need to be multiplied or divided. Failing to cancel units properly can lead to incorrect calculations and final answers.
- Using incorrect prefixes: Unit systems often involve the use of prefixes such as milli, kilo, and mega. Using the wrong prefix can result in incorrect calculations and final answers. It is important to pay attention to the given units and apply the correct prefixes accordingly.
To avoid these common mistakes, it is important to carefully read and analyze the given problem, identify the desired units, and apply the appropriate conversion factors. It can also be helpful to double-check calculations and ensure that units are canceled properly throughout the problem. Practice and familiarity with unit systems will also help in avoiding these mistakes and improving accuracy in homework assignments.