
Geometry is a branch of mathematics that studies the properties and relationships of shapes, sizes, and positions. It plays a fundamental role in many fields, including architecture, engineering, and computer graphics. Whether you are a student preparing for an exam or an adult looking to refresh your knowledge, having access to a comprehensive answer key can help you understand and master the concepts of geometry.
With a geometry review answer key, you can check your understanding of various topics such as angles, lines, polygons, and circles. It provides you with the correct solutions and explanations to help you learn from your mistakes and improve your problem-solving skills. The answer key serves as a valuable tool to reinforce your understanding of geometric principles and ensure that you are on the right track in your studies.
Geometry review answer keys are especially beneficial for self-study or supplemental resources. They allow you to work through practice questions at your own pace, without the pressure of time constraints. By referring to the answer key, you can verify your solutions, gain confidence in your abilities, and build a solid foundation in geometry. Additionally, the answer key can provide alternative approaches and strategies to solving problems, allowing you to broaden your problem-solving repertoire.
Whether you are a student, teacher, or someone who simply enjoys exploring mathematical concepts, having a reliable geometry review answer key can enhance your learning experience. It provides a structured approach to mastering geometry and empowers you to tackle challenging problems with confidence. By diligently practicing and referring to the answer key, you can strengthen your geometric skills and develop a deeper understanding of this fascinating field of mathematics.
Geometry Review Answer Key

In the subject of geometry, it is important to review and understand various concepts and formulas. This answer key serves as a guide to check your solutions and ensure that you have correctly solved the problems. By checking your answers, you can identify any areas where you may need further practice or understanding.
Points, Lines, and Planes:
- A point is a location in space that has no size or shape.
- A line is a set of points that extends infinitely in both directions.
- A plane is a flat surface that extends infinitely in all directions.
Angles:
- An angle is formed by two rays that share a common endpoint, called the vertex.
- The measure of an angle is given in degrees, with a full circle measuring 360 degrees.
- Vertical angles are formed by the intersection of two lines and are congruent.
Triangles:
- A triangle is a polygon with three sides.
- The sum of the interior angles of a triangle is always 180 degrees.
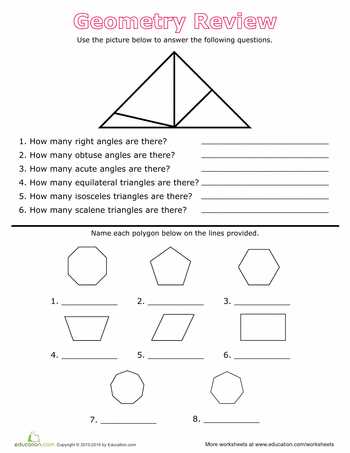
- Triangles can be classified by their sides (equilateral, isosceles, scalene) or by their angles (acute, obtuse, right).
Circles:
- A circle is a set of points in a plane that are equidistant from a given point called the center.
- The diameter of a circle is a line segment that passes through the center and has endpoints on the circle.
- The circumference of a circle is the distance around the circle and can be found using the formula C = 2πr, where r is the radius.
By reviewing and understanding these key concepts, you will have a solid foundation in geometry and be able to solve a variety of problems. Keep practicing and applying these principles to further develop your skills in geometry.
Understanding Geometric Concepts
In order to have a strong foundation in geometry, it is important to understand key geometric concepts. These concepts provide the building blocks for solving more complex problems and understanding the relationships between different shapes and figures.
Points are the most basic geometric concept. They are represented by a dot and have no size or dimension. Points are used to define other geometric objects like lines, segments, and polygons.
A line is a straight path that extends infinitely in both directions. It is defined by two points, and any two points on a line can be connected to form a segment, which is a portion of the line with definite endpoints.
A plane is a flat surface that extends infinitely in all directions. It is defined by three non-collinear points, and any three points on a plane determine a unique plane.
- A triangle is a polygon with three sides. It is defined by three non-collinear points, called vertices.
- A quadrilateral is a polygon with four sides. It is defined by four points, and its vertices can be connected to form line segments.
- A circle is a round shape with no edges or corners. It is defined by a center point and a radius, which is the distance from the center to any point on the circle.
Understanding these geometric concepts is essential for solving problems and proving theorems in geometry. By mastering these concepts, one can develop a deeper understanding of the properties and relationships of various geometric shapes and figures.
Geometric Shapes and Figures
A geometric shape is a figure that occupies a specific area in space. These shapes are characterized by their different attributes such as sides, angles, and symmetry. Understanding and recognizing geometric shapes is essential in various fields, including mathematics, architecture, and design.
1. Polygons: Polygons are closed figures with straight sides. Examples of polygons include triangles, quadrilaterals, pentagons, hexagons, and so on. Each polygon has its own unique set of properties, such as the sum of its interior angles and the number of sides it has.
2. Circles: Circles are perfectly round shapes defined by a continuous curve. They are characterized by their radius (the distance between the center and any point on the circle) and their diameter (twice the radius). Circles have no corners or straight sides.
3. Rectangles: Rectangles are quadrilaterals with four right angles. They have opposite sides that are parallel and equal in length. The area of a rectangle can be calculated by multiplying its length by its width, and its perimeter is the sum of all its sides.
4. Triangles: Triangles are three-sided polygons. They can be classified based on the length of their sides (e.g., equilateral, isosceles, or scalene) or the measure of their angles (e.g., acute, right, or obtuse). The area of a triangle can be determined using the formula A = 1/2 base × height.
5. Quadrilaterals: Quadrilaterals are four-sided polygons. They can be categorized into various types such as squares, rectangles, parallelograms, trapezoids, and rhombuses. Each type has its own unique properties and formulas to calculate their area and perimeter.
- Squares: Squares are quadrilaterals with four equal sides and four right angles. The area of a square can be found by squaring the length of one of its sides.
- Parallelograms: Parallelograms have opposite sides that are parallel and equal in length. Their area can be calculated by multiplying the base by the height.
- Trapezoids: Trapezoids have one pair of parallel sides. The area of a trapezoid can be determined using the formula A = 1/2 (sum of the bases) × height.
- Rhombuses: Rhombuses have four equal sides but no right angles. The area of a rhombus can be found by multiplying the lengths of its diagonals and dividing by 2.
Understanding the properties and characteristics of different geometric shapes and figures is essential for solving problems and analyzing spatial relationships. It allows us to calculate areas, perimeters, volumes, and more, making geometry a fundamental branch of mathematics.
Properties of Geometric Figures
The study of geometry involves understanding the properties of different geometric figures. These properties help us to describe and classify shapes, and allow us to solve various problems related to measurement, area, and volume. Here are some important properties of geometric figures:
- Angles: An angle is formed by two intersecting lines or line segments. It is measured in degrees, and can be classified as acute (less than 90 degrees), right (exactly 90 degrees), obtuse (more than 90 degrees but less than 180 degrees), or straight (exactly 180 degrees).
- Sides: The sides of a geometric figure are the line segments that form its boundaries. They can be classified based on their length, such as equal sides (congruent), unequal sides, or parallel sides.
- Vertices: Vertices are the points where the sides of a geometric figure intersect. The number of vertices determines the shape of the figure. For example, a triangle has three vertices, while a quadrilateral has four vertices.
- Diagonals: Diagonals are line segments that connect nonadjacent vertices of a polygon. They can be used to divide the polygon into different regions, and their lengths can be calculated using methods of trigonometry or Pythagorean theorem.
- Symmetry: Symmetry refers to a figure that can be divided into two equal halves that mirror each other. Figures can have different types of symmetry, such as line symmetry (reflection symmetry) or rotational symmetry.
These are just a few of the many properties that help us understand and analyze geometric figures. By studying these properties, mathematicians and scientists are able to solve real-world problems and make important discoveries in various fields of study.
Triangles
A triangle is a polygon with three sides, three angles, and three vertices. It is one of the most fundamental shapes in geometry and has many important properties and formulas associated with it.
In terms of sides, triangles can be classified into three categories: equilateral, isosceles, and scalene. An equilateral triangle has three equal sides, an isosceles triangle has two equal sides, and a scalene triangle has no equal sides.
The angles of a triangle also have their own classifications. A triangle can be classified as acute, right, or obtuse based on the measures of its angles. An acute triangle has all angles less than 90 degrees, a right triangle has one angle that measures exactly 90 degrees, and an obtuse triangle has one angle greater than 90 degrees.
Triangle formulas are used to calculate various properties of triangles. The most well-known formula is the Pythagorean theorem, which states that in a right triangle, the square of the length of the hypotenuse is equal to the sum of the squares of the lengths of the other two sides.
Triangles also play a crucial role in trigonometry, where the ratios of the sides of a right triangle are used to calculate angles and lengths. Additionally, triangles are an integral part of many geometric proofs and constructions.
Overall, triangles are an essential concept in geometry that have numerous applications and properties. Understanding the different types of triangles, their angles, and formulas is necessary for solving geometry problems and advancing in the study of mathematics.
Types of Triangles
Triangles are three-sided polygons. They can be categorized into different types based on their side lengths and angle measurements. Understanding the different types of triangles is essential in geometry as it helps to identify and solve various geometric problems. Here are some essential types of triangles:
Equilateral Triangle
An equilateral triangle is a triangle with all three sides of equal length. Since all sides are equal, all three angles in an equilateral triangle are also equal, measuring 60 degrees. It is the only type of triangle that has this property. Equilateral triangles are often used in architecture and engineering for their stability and symmetry.
Isosceles Triangle
An isosceles triangle has two sides of equal length. The third side, called the base, is of different length. The angles opposite the equal sides are also equal. The angle opposite the base may be different. Isosceles triangles are commonly seen in real-life objects, such as the roofs of houses or the wings of airplanes.
Scalene Triangle
A scalene triangle is a triangle with no sides of equal length. All three angles in a scalene triangle are also different in measurement. Scalene triangles can have various angle combinations, making them versatile in geometry problem-solving.
Right Triangle
A right triangle has one angle measuring 90 degrees, which is called the right angle. The other two angles are acute angles, measuring less than 90 degrees each. The side opposite the right angle is called the hypotenuse, and it is the longest side in a right triangle. The Pythagorean Theorem is often used to solve problems involving right triangles.
Triangle Properties and Formulas
Triangles are one of the fundamental shapes in geometry, and understanding their properties and formulas is crucial for solving problems related to them. Here are some key concepts:
Types of Triangles:
- Equilateral Triangle: All three sides are equal in length.
- Isosceles Triangle: Two sides are equal in length.
- Scalene Triangle: No sides are equal in length.
- Right Triangle: One angle is a right angle (90 degrees).
- Obtuse Triangle: One angle is greater than 90 degrees.
- Acute Triangle: All angles are less than 90 degrees.
Perimeter: The perimeter of a triangle is the sum of the lengths of all its sides.
Area: The area of a triangle can be calculated using different formulas depending on the given information:
Area Formulas:
- Heron’s Formula: If the lengths of all three sides are known, the area can be calculated using Heron’s formula: A = √(s(s – a)(s – b)(s – c)), where s is the semi-perimeter of the triangle, and a, b, and c are the lengths of the sides.
- Base and Height: If the base and height of the triangle are known, the area can be calculated using the formula: A = (1/2) * base * height.
- Heron’s Formula with Altitudes: If the lengths of the altitudes (perpendiculars drawn from each vertex to the opposite side) are known, the area can be calculated using the formula: A = (1/2) * altitude1 * altitude2 * altitude3.
Pythagorean Theorem: In a right triangle, the sum of the squares of the lengths of the two shorter sides (legs) is equal to the square of the length of the longest side (hypotenuse). This theorem can be used to solve various problems involving right triangles.
Understanding these triangle properties and formulas can simplify the process of solving geometry problems and help in finding the relationships between different elements of a triangle.