Geometry is an important field of mathematics that deals with the study of shapes, sizes, and properties of figures. It plays a crucial role in various real-life applications, such as architecture, engineering, and design. Understanding the concepts and principles of geometry is essential to solving problems and finding solutions.
1 5 Practice B is a set of exercises aimed at reinforcing the understanding of geometry concepts and helping students practice their skills. These practice exercises provide an opportunity for students to apply the knowledge they have learned in class and test their comprehension of the subject matter. By answering the questions in Practice B, students can identify their strengths and weaknesses in geometry and work on improving their understanding.
The answers to 1 5 Practice B are valuable resources for students to check their work and verify their solutions. Having access to the correct answers allows students to self-assess their progress and identify any mistakes or misconceptions they may have. This feedback helps students to learn from their errors and make adjustments in their thinking, ultimately leading to a deeper understanding of geometry concepts.
Overall, 1 5 Practice B geometry answers are an important tool for students to reinforce their learning, practice their skills, and gain a better understanding of geometry. By utilizing these answers effectively, students can enhance their problem-solving abilities and build a solid foundation in geometry, setting them up for success in their further studies and future careers.
5 Practice B Geometry Answers: How to Solve Geometry Problems

Geometry is a branch of mathematics that deals with shapes, sizes, and properties of figures and spaces. Solving geometry problems not only requires a clear understanding of concepts and formulas, but also logical thinking and problem-solving skills. In this article, we will explore some strategies and steps to solve geometry problems using 5 practice B geometry answers.
1. Understand the problem: Read the problem carefully and make sure you understand what is being asked. Identify the given information and the required solution.
2. Draw a diagram: Visualizing the problem by drawing a diagram can help you understand the relationships between different geometric figures and angles. Use the given information to accurately represent the problem.
3. Identify relevant concepts and formulas: Review your knowledge of geometry concepts and formulas that are relevant to the problem. This could include properties of angles, triangles, circles, or equations for calculating areas and volumes.
4. Plan your solution: Based on the given information and the concepts/formulas you have identified, develop a plan for solving the problem. Determine the steps you need to take and the calculations you need to perform.
5. Execute your plan: Follow the steps you have planned and perform the necessary calculations. Be careful with your calculations and double-check your work to avoid mistakes.
6. Check your solution: Once you have found an answer, check if it makes sense in the context of the problem. Check your calculations and ensure that your answer satisfies the given conditions or constraints.
By following these steps and using the provided 5 practice B geometry answers, you can improve your problem-solving skills in geometry. Practice is key to mastering geometry, so make sure to attempt various types of problems to enhance your understanding and application of geometry concepts.
Understanding 1 5 Practice B Geometry Problems
When working on 1 5 Practice B Geometry problems, it is important to have a clear understanding of the concepts and formulas involved. Geometry is a branch of mathematics that deals with the properties and relationships of shapes, sizes, and positions of figures. It involves both visualizing and understanding the properties of different geometric shapes.
In Practice B problems, you are likely to encounter questions that involve finding the perimeter, area, or volume of various geometric figures. To solve these problems, it is crucial to identify the correct formula and apply it accurately. For example, to find the perimeter of a rectangle, you need to add the lengths of all its sides. To find the area of a triangle, you can use the formula A = 1/2 * base * height.
To succeed in solving Practice B Geometry problems, it is beneficial to familiarize yourself with different geometric shapes and their properties. This includes knowing the formulas for finding the perimeter, area, and volume of common shapes such as triangles, rectangles, circles, and cylinders.
Practice B problems often require problem-solving skills and an ability to apply geometric principles to real-life situations. Some questions may involve finding the length of an unknown side or angle in a given figure using the properties of similar triangles or applying the Pythagorean theorem to right triangles.
In summary, understanding 1 5 Practice B Geometry problems requires a solid grasp of geometric concepts, formulas, and problem-solving skills. By studying the properties of different shapes and regularly practicing problems, you can enhance your understanding and fluency in Geometry.
Step-by-Step Guide to Solve 1 5 Practice B Geometry Problems
Solving geometry problems can often be challenging, but with the right approach, you can simplify the process and find the correct answers. In this step-by-step guide, we will walk you through the process of solving 1 5 Practice B geometry problems.
1. Read the problem carefully: Before diving into solving the problem, it is crucial to understand the given information and what is being asked. Take your time to read the problem statement multiple times and identify any key phrases or numbers that are provided.
2. Identify the given information: Once you have understood the problem, identify the given information. This may include measurements of angles, lengths of sides, or any other relevant data. Write down this information in a clear and organized manner to make it easier to refer back to later.
3. Visualize the problem: Geometry problems often involve shapes and diagrams. Take a moment to visualize the problem and draw the given figure or shape, labeling any known measurements or angles. This will help you visualize the problem and make it easier to identify any unknowns.
4. Determine what needs to be found: Next, determine the unknowns in the problem. This could be the measurement of an angle, the length of a side, or any other geometric property. Write down what needs to be found so that you have a clear goal in mind.
5. Apply relevant geometry principles: Now that you have a clear understanding of what needs to be found, apply relevant geometry principles to solve the problem. This may involve using theorems, postulates, or formulas that you have learned. Use these principles to set up equations or relationships that will help you find the solution.
6. Solve the equations or relationships: With the equations or relationships set up, solve them step-by-step to find the unknowns. Depending on the complexity of the problem, this may involve simplifying equations, using algebraic manipulation, or applying known geometric properties.
7. Check your solution: Once you have found the solution, double-check your work to ensure that it is correct. Substitute the values back into the original equations or relationships to verify that they satisfy all the given conditions. If the solution does not meet the conditions, review your work and double-check for any errors.
Remember, practice makes perfect in solving geometry problems. By following this step-by-step guide and practicing regularly, you will develop a strong foundation in geometry and be able to tackle more complex problems with ease.
Key Concepts for 1 5 Practice B Geometry Problems
In the 1 5 Practice B Geometry problems, there are several key concepts to keep in mind. These concepts include angles, parallel lines, and congruence.
Angles:
Angles are an important concept in geometry. They are formed when two lines intersect, and can be classified based on their measurement. Acute angles measure less than 90 degrees, right angles measure exactly 90 degrees, obtuse angles measure between 90 and 180 degrees, and straight angles measure exactly 180 degrees. In the 1 5 Practice B Geometry problems, you may need to identify and find missing angles using the properties of angles formed by parallel lines and a transversal.
Parallel Lines:
Parallel lines are lines that never intersect and are always the same distance apart. In the 1 5 Practice B Geometry problems, you may need to identify and work with parallel lines. When two parallel lines are intersected by a transversal, several angles are formed. These angles have special properties, such as corresponding angles being congruent and alternate interior angles being congruent. Recognizing these properties can help you solve problems involving parallel lines.
Congruence:
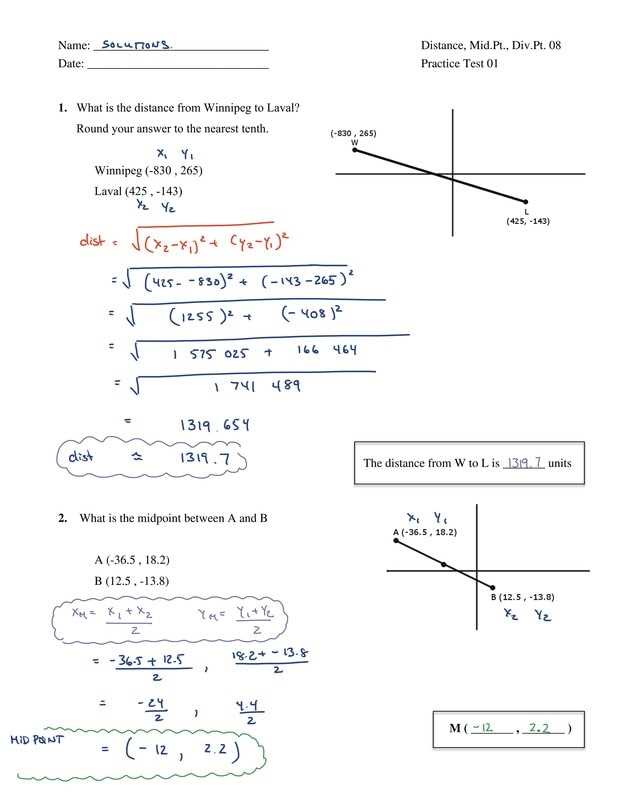
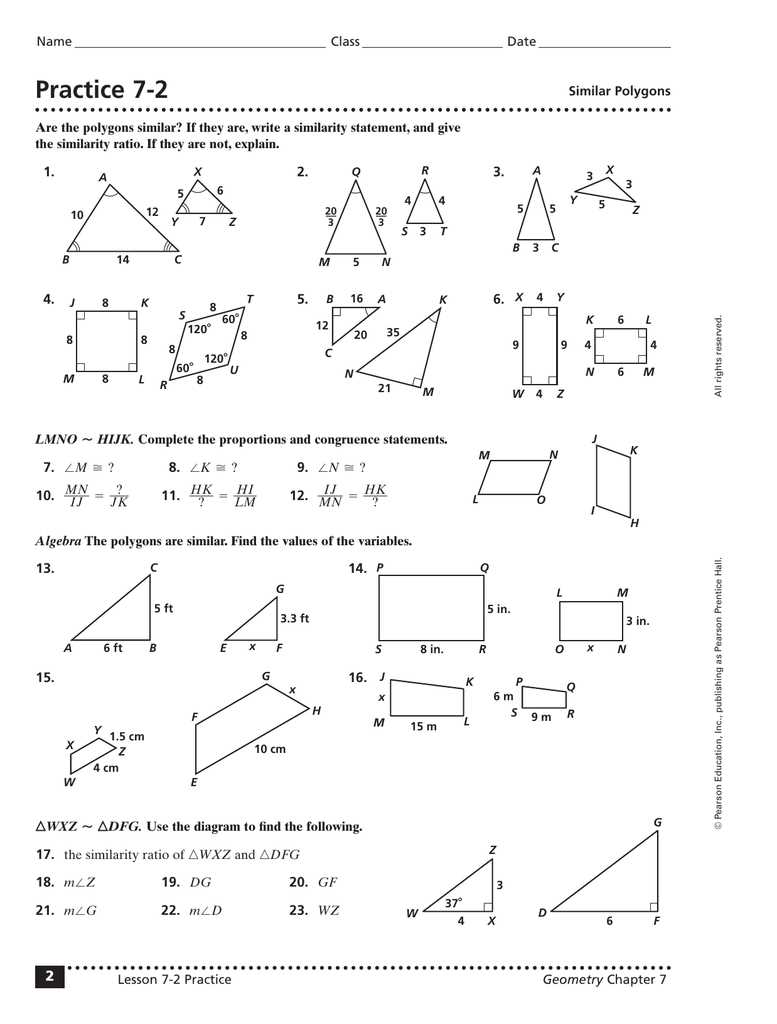
Congruence is the concept of two figures having the same shape and size. In the 1 5 Practice B Geometry problems, you may need to determine if two triangles or other figures are congruent. This can be done by identifying corresponding sides and angles and using congruence postulates, such as Side-Side-Side (SSS), Side-Angle-Side (SAS), and Angle-Angle-Side (AAS).
By understanding these key concepts of angles, parallel lines, and congruence, you will be better prepared to tackle the 1 5 Practice B Geometry problems and successfully solve them. Remember to carefully read and analyze each problem, identify the relevant concepts, and apply the appropriate formulas and theorems to find the solution.
Common Mistakes to Avoid in 1 5 Practice B Geometry Problems
When working on the 1 5 Practice B geometry problems, it’s important to be aware of common mistakes that students often make. By being mindful of these mistakes, you can improve your problem-solving skills and ensure accuracy in your answers.
1. Not understanding the problem
One common mistake is not fully understanding the given problem. It’s crucial to carefully read and comprehend the problem statement, identifying the given information and what is being asked. Take the time to break down the problem and visualize the given information to develop a clear plan of action.
2. Misinterpreting or ignoring the diagram
The diagram provided in 1 5 Practice B geometry problems is a valuable tool for understanding the problem. However, students often make the mistake of misinterpreting or ignoring important details in the diagram. Pay close attention to labels, lengths, and angles in the diagram, as they provide essential information for solving the problem.
3. Incorrectly applying geometric principles
Geometry problems require a solid understanding and application of geometric principles and formulas. One common mistake is incorrectly applying these principles or using the wrong formulas. Make sure to review and understand the relevant geometric concepts, such as the Pythagorean theorem, angle relationships, and area formulas, to solve problems accurately.
4. Lack of precision in calculations
Another common mistake is being careless with calculations, leading to inaccuracies in the final answer. Make sure to double-check your arithmetic, use proper units, and round answers appropriately. Paying attention to detail and using precision in calculations will help you achieve more accurate results.
5. Missing or incomplete solution
Lastly, it’s important to provide a complete and thorough solution in 1 5 Practice B geometry problems. A common mistake is omitting important steps or not providing a clear explanation of your reasoning. Make sure to show all the steps in your solution and clearly communicate your thought process to ensure a comprehensive answer.
Avoiding these common mistakes will help you improve your problem-solving skills and achieve accurate answers in 1 5 Practice B geometry problems. By understanding the problem, utilizing the diagram effectively, applying the correct geometric principles, being precise in calculations, and providing a comprehensive solution, you will be able to tackle these problems with confidence.
Tips and Tricks for Faster Solutions in 1 5 Practice B Geometry Problems

In geometry problems, it is important to have a clear understanding of the concepts involved and be able to visualize the figures accurately. Here are some tips and tricks that can help you to solve 1 5 Practice B geometry problems more efficiently.
1. Clearly identify the given information
Before attempting to solve a problem, carefully read and understand the given information. Identify what is being asked and what information is provided. Highlight or underline key details to keep track of them when solving the problem.
2. Draw accurate diagrams
In geometry, diagrams are crucial for understanding and solving problems. Take the time to draw accurate and proportional diagrams, labeling the given information and any additional information you may need to solve the problem. This will help you visualize the problem and make it easier to find the solution.
3. Use known theorems and formulas
Geometry has many theorems and formulas that can be applied to solve problems. Familiarize yourself with these theorems and formulas, and use them to your advantage. If you encounter a problem that seems difficult, try to identify any relevant theorems or formulas that may be applicable.
4. Look for patterns and symmetries
Patterns and symmetries can often provide clues for solving geometry problems. Look for repeating shapes, angles, or sides that may be related in some way. Symmetrical figures can also provide information about angles or lengths. By recognizing these patterns, you can simplify the problem and find the solution more quickly.
5. Break down complex problems into smaller parts
If a problem seems overwhelming, break it down into smaller, more manageable parts. Solve each part individually and then combine the results. This can make the problem more approachable and help you avoid feeling overwhelmed.
6. Practice with similar problems
The more you practice solving geometry problems, the better you will become at recognizing patterns and applying theorems and formulas. Look for additional practice problems that are similar to the ones in 1 5 Practice B and challenge yourself to solve them efficiently. With practice, you will improve your problem-solving skills and be able to solve geometry problems more quickly.
By following these tips and tricks, you can improve your efficiency in solving 1 5 Practice B geometry problems and feel more confident in approaching similar problems in the future.