
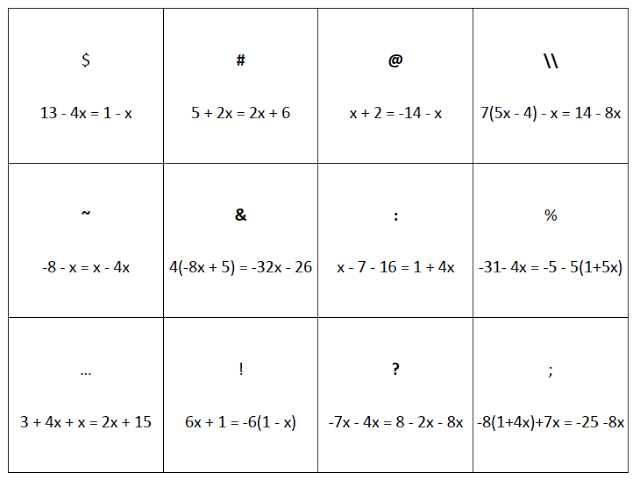
When solving equations with variables on both sides, it can sometimes be challenging to determine the correct steps to take. However, with the help of this answer key, you can easily solve these types of equations and verify your answers.
Equations with variables on both sides often involve combining like terms, using the distributive property, and applying inverse operations to isolate the variable. This answer key will guide you through each step of the process, ensuring that you arrive at the correct solution.
By providing detailed explanations and step-by-step solutions, this answer key will help you understand the logic behind solving equations with variables on both sides. It will also allow you to practice your problem-solving skills and gain confidence in tackling more complex equations in the future.
Whether you are a student learning algebra or an educator looking for additional resources, this answer key is a valuable tool for mastering the concept of solving equations with variables on both sides. With practice, patience, and the help of this answer key, you will become proficient in solving these types of equations and be well-equipped for success in your mathematical journey.
The Basics of Solving Equations with Variables on Both Sides
Solving equations with variables on both sides can initially seem challenging, but with a basic understanding of the steps involved, it becomes much easier to navigate through the process. The key is to isolate the variable by performing the same operations on both sides of the equation.
Let’s start with a simple example to illustrate the process. Consider the equation: 3x + 7 = 2x – 4. The first step is to combine like terms on both sides of the equation. In this case, we have 3x and 2x, which are like terms. By subtracting 2x from both sides, we eliminate the 2x term on the right side, resulting in x + 7 = -4.
Next, we want to get the variable, x, alone on one side. To do this, we need to eliminate the constant term, 7, on the left side. By subtracting 7 from both sides, we are left with x = -11. This is our final answer.
In more complex examples, it’s important to follow the same steps of combining like terms and isolating the variable. Sometimes, it may be necessary to perform additional operations such as multiplying or dividing both sides of the equation by a constant to eliminate a coefficient. The goal is always to end up with the variable on one side and a constant on the other.
Remember, practice makes perfect when it comes to solving equations with variables on both sides. It’s important to familiarize yourself with the process and seek out additional examples to reinforce your understanding. With time and practice, solving equations with variables on both sides will become second nature.
Understanding the concept of equations with variables on both sides and their importance in problem-solving
Equations with variables on both sides are a fundamental concept in algebra. In these types of equations, the variable is present on both sides of the equation, making it necessary to perform operations to isolate the variable and find its value. Solving equations with variables on both sides is an essential skill that is used in various real-world situations and is crucial for problem-solving in mathematics.
When encountering an equation with variables on both sides, it is important to understand that the goal is to isolate the variable by performing operations that maintain the equality of the equation. This involves simplifying the equation and rearranging the terms until the variable is separated on one side of the equation. By understanding the basic principles of algebraic manipulation, such as combining like terms and applying inverse operations, one can successfully solve equations with variables on both sides and determine the value of the variable.
One key importance of solving equations with variables on both sides lies in its application to real-world problems. Many real-world situations can be modeled using equations, and often these equations involve variables on both sides. For example, in financial planning, equations with variables on both sides can be used to calculate monthly expenses and income, allowing individuals to make informed decisions about budgeting and saving.
Furthermore, solving equations with variables on both sides helps develop critical thinking and problem-solving skills. These types of equations require careful analysis and strategy to determine the most effective steps and operations to isolate the variable. By solving equations with variables on both sides, individuals develop the ability to approach complex problems systematically, break them down into simpler steps, and apply logical reasoning to find a solution.
In conclusion, understanding equations with variables on both sides is crucial in both practical applications and building problem-solving skills. By mastering this concept, individuals gain the ability to effectively solve complex equations and apply these skills to various real-world scenarios.
Step-by-Step Guide to Solving Equations with Variables on Both Sides
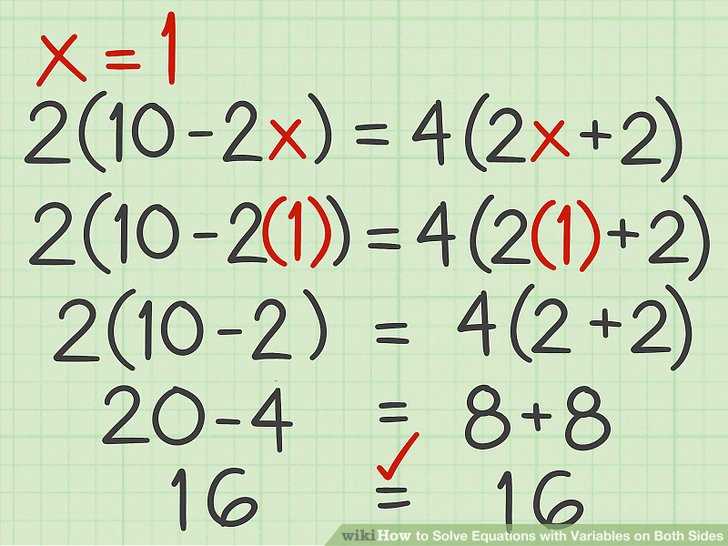
Solving equations with variables on both sides can seem challenging at first, but by following a step-by-step guide, you can easily find the solution. In this guide, we will break down the process into simple steps to help you understand and solve these types of equations effectively.
Step 1: Combine Like Terms
The first step is to combine like terms on both sides of the equation. Like terms are terms that have the same variable and exponent. Simplify the equation by adding or subtracting the like terms to create a simpler equation.
Step 2: Move the Variables to One Side
In this step, you need to move all the variables to one side of the equation. To do this, you can either subtract or add the variable terms on one side and move them to the other side. This step will help you isolate the variables and prepare for the next step.
Step 3: Move the Constants to the Other Side
After isolating the variables in the previous step, you need to focus on moving the constants to the other side of the equation. By adding or subtracting the constant terms on one side, you can relocate them to the opposite side of the equation.
Step 4: Simplify Further
Once you have moved the variables and constants to their respective sides, simplify the equation further by combining like terms once again. This step will help you create an equation that contains only the variable on one side and the constant on the other side.
Step 5: Solve for the Variable
The final step is to solve for the variable by performing the necessary mathematical operations. Follow the order of operations, such as multiplication, division, addition, and subtraction, to find the value of the variable. Remember to perform the same operations on both sides of the equation to maintain balance.
Step 6: Check Your Solution
Always check your solution by plugging it back into the original equation. Substitute the value of the variable into the equation and see if the equation holds true. If it does, then you have found the correct solution. If not, retrace your steps and look for any mistakes you may have made along the way.
By following this step-by-step guide, you can tackle equations with variables on both sides efficiently. Practice with different examples to enhance your understanding and problem-solving skills.
A detailed explanation of the necessary steps to solve equations with variables on both sides
When solving equations with variables on both sides, it is important to follow a systematic approach to ensure accuracy and efficiency. The following steps outline the necessary process:
- Identify the variable terms: Look for terms that contain the variable on both sides of the equation. These are the terms that need to be combined and simplified.
- Move the variable terms to one side: In order to isolate the variable, move all the variable terms from one side of the equation to the other. To do this, perform the opposite operation on both sides of the equation. For example, if there is a variable term with a positive coefficient on the left side and a variable term with a negative coefficient on the right side, subtract the variable term with the negative coefficient from both sides.
- Combine like terms: Once the variable terms are on one side of the equation, combine like terms (terms with the same variable and exponent) on that side. Simplify the expression as much as possible.
- Move the constant terms to the other side: After simplifying the expression on the side with the variable terms, move the constant terms (terms without variables) to the other side of the equation. Perform the opposite operation to what is already present on that side. For example, if there is a positive constant on the side with the variable terms, subtract it from both sides.
- Combine the constant terms: Once the constant terms are on one side of the equation, combine them as much as possible. Simplify the expression further.
- Isolate the variable: At this point, there should only be the variable term on one side of the equation. Perform any necessary operations to isolate the variable, such as dividing both sides by the coefficient of the variable term.
- Check the solution: Finally, substitute the found solution back into the original equation to check its validity. If both sides of the equation are still equal after substituting the solution, then it is the correct solution.
By following these steps, equations with variables on both sides can be solved accurately and efficiently. It is important to carefully perform each step and check for any potential errors along the way to ensure the correctness of the final solution.
Common Challenges in Solving Equations with Variables on Both Sides
When solving equations with variables on both sides, there are several common challenges that students often face. One challenge is dealing with multiple variables on each side of the equation. It can be confusing to determine which variable to solve for first and how to simplify the equation by combining like terms.
Another challenge is understanding the concept of balancing equations. In these types of equations, it is important to maintain the equality between both sides by performing the same operations on both sides. Students may struggle with identifying the correct operations to perform and ensuring that they are applied correctly.
Additionally, solving equations with variables on both sides often involves using the distributive property. This property allows for the multiplication of a term to be distributed to each term within a set of parentheses. Understanding when and how to use the distributive property can be challenging for students and may require additional practice and explanation.
An important aspect of solving equations with variables on both sides is keeping track of all the steps and simplifications made. It is crucial to maintain accuracy and avoid making arithmetic errors, as even a small mistake can lead to an incorrect solution. Students should double-check their work and use strategies such as substitution or backtracking to verify the correctness of their solutions.
In summary, solving equations with variables on both sides can present challenges in identifying which variable to solve for first, balancing equations, understanding the distributive property, and maintaining accuracy throughout the solving process. It is important for students to practice these skills and seek guidance when needed to improve their proficiency in solving these types of equations.
Identifying and addressing common difficulties encountered when solving equations with variables on both sides
Solving equations with variables on both sides can be challenging for many students. There are several common difficulties that students may encounter while working with these types of equations. By identifying these difficulties, educators can better address and support students in their learning process.
1. Incorrectly distributing terms: One common difficulty is when students incorrectly distribute terms across both sides of the equation. This can lead to errors in simplification and ultimately incorrect solutions. To address this, educators can provide ample practice and reinforcement on the distributive property and guide students through step-by-step examples.
2. Forgetting to combine like terms: Another challenge is when students forget to combine like terms before solving the equation. This can result in unnecessary complexity and difficulty in finding the correct solution. Educators can address this by emphasizing the importance of combining like terms and providing practice problems that specifically target this skill.
3. Mistakes in the steps of solving: Students may also make mistakes in the steps of solving equations with variables on both sides. For example, they may forget to perform the same operation on both sides of the equation or skip certain steps altogether. To address this, educators can provide clear guidelines and step-by-step instructions, as well as offer opportunities for students to correct their mistakes and learn from them.
4. Misunderstanding the concept of equivalent equations: Understanding the concept of equivalent equations is crucial in solving equations with variables on both sides. Students may struggle with recognizing when two equations are equivalent or may mistakenly believe that the solutions to both equations are the same. Educators can address this by providing examples and explanations that illustrate the concept of equivalent equations, as well as encouraging students to check their solutions in the original equation to verify their correctness.
In conclusion, identifying the common difficulties that students encounter when solving equations with variables on both sides is essential for effective instruction and support. By addressing these difficulties through targeted instruction, practice, and reinforcement, educators can help students develop a strong foundation in solving these types of equations.