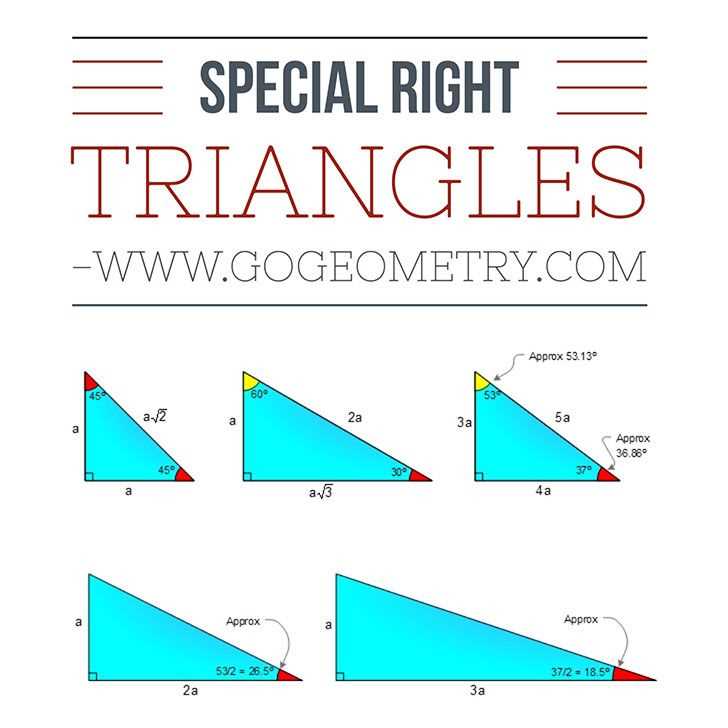
Special right triangles are a topic of interest in geometry, known for their unique properties and applications. These triangles, namely the 45-45-90 and the 30-60-90 triangles, have angles that create specific ratios between their sides.
In the 45-45-90 triangle, the two legs are congruent, and the hypotenuse is the length of one of the legs multiplied by √2. This ratio allows for calculations and simplifications that make solving problems involving this triangle much easier.
The 30-60-90 triangle has angles measuring 30, 60, and 90 degrees. Its sides also have specific ratios – the length of the shorter leg is half the length of the hypotenuse, and the length of the longer leg is √3 times the length of the shorter leg. These relationships can be incredibly useful in various geometric and trigonometric calculations.
Understanding and being able to apply the properties of special right triangles is essential for solving geometry problems efficiently. By recognizing these triangles and utilizing their ratios, you can simplify complex calculations and find solutions more easily.
Special Right Triangles Puzzle Answers
If you’ve been struggling with special right triangles puzzles, fret no more. We have the answers you’ve been looking for. Solving these puzzles often involves applying the properties of special right triangles, such as the 45-45-90 and 30-60-90 triangles.
Let’s take a look at some common special right triangles and their answers:
-
45-45-90 Triangle: In a 45-45-90 triangle, the two legs are congruent, and the hypotenuse is equal to the length of the leg multiplied by the square root of 2. So, if one leg has a length of 4, the hypotenuse will be 4√2.
-
30-60-90 Triangle: In a 30-60-90 triangle, the hypotenuse is twice the length of the shortest leg, and the length of the longer leg can be found by multiplying the shortest leg by the square root of 3. For example, if the shortest leg has a length of 3, the hypotenuse will be 6, and the longer leg will be 3√3.
-
Pythagorean Triples: Pythagorean triples are sets of three positive integers that satisfy the Pythagorean theorem. Some common examples include (3, 4, 5) and (5, 12, 13). These triples can be used to solve special right triangles puzzles by finding the missing side lengths.
With these answers in hand, you’ll be well-equipped to tackle any special right triangles puzzle that comes your way. Remember to apply the properties of the triangles and use the given information to solve for the missing side lengths. Good luck!
Identifying Special Right Triangles
In geometry, special right triangles are triangles that have specific characteristics and properties. These triangles have angles and side lengths that can be easily identified and calculated without using trigonometric functions. Understanding and identifying special right triangles can help solve geometric problems more efficiently.
There are two types of special right triangles: the 45-45-90 triangle and the 30-60-90 triangle. These triangles have angles that are multiples of 30 and 45 degrees, making them easier to recognize.
45-45-90 Triangle
The 45-45-90 triangle is an isosceles triangle, which means that it has two congruent sides and two congruent angles. In this triangle, the two legs (the sides opposite the 45-degree angles) are equal in length, and the hypotenuse (the side opposite the right angle) is √2 times the length of the legs. This relationship allows us to easily calculate the side lengths of the triangle.
- The ratio of the lengths of the sides in a 45-45-90 triangle is:
- Leg length: l
- Hypotenuse length: √2 * l
30-60-90 Triangle
The 30-60-90 triangle is also a special right triangle. In this triangle, the angles measure 30 degrees, 60 degrees, and 90 degrees. The side lengths of this triangle follow a specific ratio, which makes it easy to identify and calculate the lengths of the sides.
- The ratio of the lengths of the sides in a 30-60-90 triangle is:
- Shortest leg length: l
- Longer leg length: √3 * l
- Hypotenuse length: 2l
By recognizing and understanding the properties of these special right triangles, solving geometric problems becomes much simpler and more efficient. These triangles serve as building blocks for more complex geometric concepts and calculations.
45-45-90 Triangle Solution
A 45-45-90 triangle is a special type of right triangle where the two legs are congruent, and the angles formed by the legs and the hypotenuse are 45 degrees each. It is a commonly encountered triangle in mathematics and has some distinctive properties and characteristics that make it easier to work with than other types of triangles.
To find the solution to a 45-45-90 triangle, we can use the relationships between the sides and angles. The length of each leg is equal to the square root of 2 times the length of the hypotenuse. This can be written as:
Leg length = √2 × Hypotenuse length
Similarly, the length of the hypotenuse is equal to the square root of 2 times the length of each leg. This can be written as:
Hypotenuse length = √2 × Leg length
Using these relationships, we can easily find the lengths of the sides of a 45-45-90 triangle if we know the length of one of the sides. For example, if we are given the length of one leg of the triangle, we can use the formula to find the lengths of the other leg and the hypotenuse.
In addition to these properties, the 45-45-90 triangle is also an isosceles triangle, meaning that it has two congruent sides and two congruent angles. This makes it useful for solving various geometric and trigonometric problems, as its symmetry and easy-to-work-with ratios simplify calculations.
30-60-90 Triangle Solution
In geometry, a 30-60-90 triangle is a special right triangle with angle measures of 30, 60, and 90 degrees. It is called a 30-60-90 triangle because the angles involved form a ratio of 1:2:√3.
For a 30-60-90 triangle, the side lengths are related by the following proportions:
- The length of the shorter leg (opposite the 30-degree angle) is equal to half the length of the hypotenuse.
- The length of the longer leg (opposite the 60-degree angle) is equal to the length of the hypotenuse multiplied by √3.
- The length of the hypotenuse (opposite the 90-degree angle) is the longest side and is always the side opposite the right angle.
This special right triangle comes in handy when dealing with trigonometry problems involving angles of 30 or 60 degrees. By knowing the ratios of the side lengths, you can easily determine the lengths of the sides without having to use the Pythagorean theorem.
Here is a table summarizing the relationships between the angles and side lengths of a 30-60-90 triangle:
| Angle | Side Opposite | Length |
|---|---|---|
| 30 degrees | Shorter leg | 1 |
| 60 degrees | Longer leg | √3 |
| 90 degrees | Hypotenuse | 2 |
By understanding and applying the properties of a 30-60-90 triangle, you can quickly solve problems involving these types of triangles.
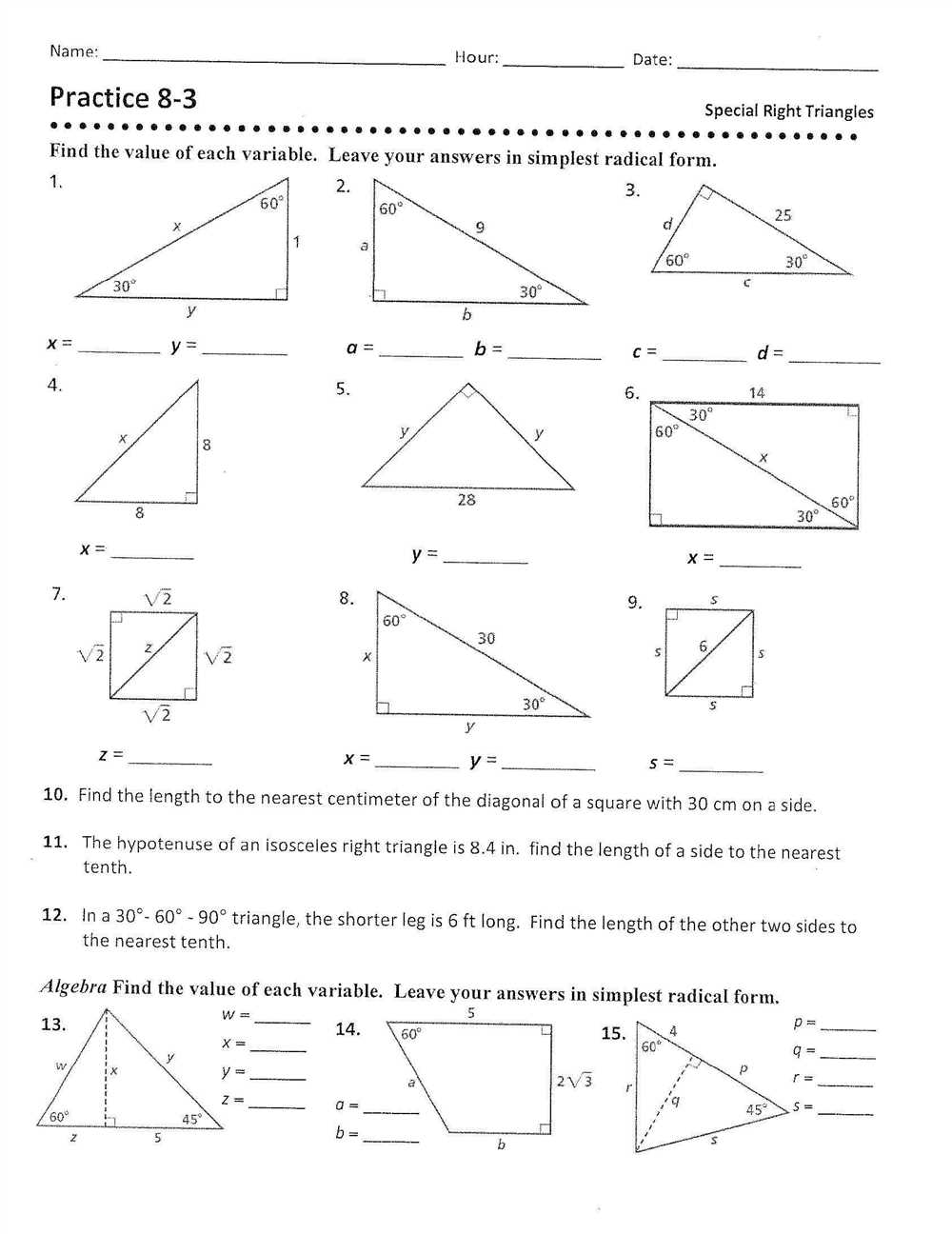
Solving for Missing Side Lengths

In special right triangles, such as the 45-45-90 or 30-60-90 triangles, there are specific relationships between the lengths of the sides. These relationships can be used to solve for missing side lengths.
For example, in a 45-45-90 triangle, the two legs are congruent, and the hypotenuse is equal to the length of a leg multiplied by √2. Therefore, if we know the length of one leg, we can easily find the lengths of the other two sides.
The same concept applies to a 30-60-90 triangle. Here, the longer leg is equal to the shorter leg multiplied by √3, and the hypotenuse is equal to the shorter leg multiplied by 2. By knowing the length of one side, we can determine the lengths of the other two sides.
To solve for missing side lengths, the given information can be used to set up an equation based on these relationships. Then, the equation can be simplified and solved to find the unknown value.
In some cases, trigonometric functions such as sine, cosine, and tangent can also be used to find missing side lengths. These functions relate the ratios of sides in a right triangle to the angles. By knowing an angle and one side length, the trigonometric function can be used to solve for the missing side length.
Overall, solving for missing side lengths in special right triangles involves using the relationships between the sides or applying trigonometric functions to set up and solve equations. Understanding these relationships and functions is essential in solving special right triangle puzzles and problems.
Finding Angle Measures

When working with special right triangles, one important task is to find the measures of the angles. This can be done using various methods, but the most common approach is to use the trigonometric ratios: sine, cosine, and tangent.
The sine function (sin) of an angle is defined as the ratio of the length of the side opposite to the angle to the length of the hypotenuse. The cosine function (cos) is defined as the ratio of the length of the side adjacent to the angle to the length of the hypotenuse. And the tangent function (tan) is defined as the ratio of the length of the side opposite to the angle to the length of the side adjacent to the angle.
- To find the measure of an angle in a right triangle, you can use the inverse trigonometric functions: arcsin, arccos, and arctan. For example, if you know the lengths of the two sides of a right triangle, you can use the inverse sine function to find the measure of one of the angles.
- Another method to find angle measures in special right triangles is by using the properties of the triangle itself. For example, in a 30-60-90 triangle, the angles are always in the ratio of 1:2:3, which means that the measures of the angles are 30 degrees, 60 degrees, and 90 degrees, respectively.
- You can also use the Pythagorean theorem to find angle measures in right triangles. This theorem states that in a right triangle, the square of the length of the hypotenuse is equal to the sum of the squares of the lengths of the other two sides. By using this theorem, you can find the lengths of the sides and then calculate the angles using the trigonometric ratios.
In conclusion, finding angle measures in special right triangles requires using trigonometric ratios, inverse trigonometric functions, properties of the triangle, and the Pythagorean theorem. By using these methods, you can accurately determine the measures of the angles and solve various problems related to special right triangles.
Using Special Right Triangles in Real Life Applications
Special right triangles, such as the 45-45-90 and the 30-60-90 triangles, have important applications in various fields of everyday life. These triangles are called “special” because they have unique properties and ratios that can be used to solve complex problems.
One real-life application of special right triangles can be found in architecture and construction. When designing buildings, architects often need to find the lengths of sides or the angles of triangular structures. By recognizing the patterns and ratios of special right triangles, architects can quickly and accurately determine these measurements without needing to perform lengthy calculations.
Another field where special right triangles are frequently used is engineering, particularly in electrical engineering. Engineers often deal with circuits and components that have specific angles and ratios. Understanding the properties of special right triangles enables engineers to easily calculate values related to voltage, current, and resistance, helping them design and analyze electrical circuits efficiently.
Special right triangles also find applications in navigation and surveying. Imagine you are standing at a point and need to measure the height of a tall building or a distant mountain. By using a clinometer to measure the angle of elevation and knowing the distance from the object, you can apply the trigonometric ratios of special right triangles to calculate the height accurately.
In summary, special right triangles are not just theoretical concepts; they have practical applications in various fields. Whether you are an architect, engineer, or navigator, understanding and utilizing the properties of special right triangles can greatly simplify and enhance your work.
Properties of Special Right Triangles
Special right triangles are a specific type of triangle that have unique geometrical properties. These triangles have angles that are considered special, and their side lengths follow distinct patterns. By understanding the properties of special right triangles, we can easily solve problems and find missing side lengths or angles.
There are two main types of special right triangles: the 45-45-90 triangle and the 30-60-90 triangle. The 45-45-90 triangle, also known as an isosceles right triangle, has two congruent angles of 45 degrees and one right angle of 90 degrees. In this triangle, the lengths of the sides follow the pattern: the length of the hypotenuse is equal to the length of one of the legs multiplied by the square root of 2.
45-45-90 Triangle
- Two congruent angles: 45 degrees
- One right angle: 90 degrees
- Side lengths follow the pattern:
- Length of hypotenuse = Length of leg * √2
On the other hand, the 30-60-90 triangle, also known as an equilateral right triangle, has angles of 30 degrees, 60 degrees, and 90 degrees. In this triangle, the side lengths also follow a specific pattern: the length of the shorter leg is equal to half the length of the hypotenuse, and the length of the longer leg is equal to the length of the shorter leg multiplied by the square root of 3.
30-60-90 Triangle
- Angles: 30 degrees, 60 degrees, 90 degrees
- Side lengths follow the pattern:
- Length of shorter leg = 1/2 * Length of hypotenuse
- Length of longer leg = Length of shorter leg * √3
Knowing these properties, we can easily solve for missing side lengths or angles in special right triangles by applying the appropriate formulas. These triangles are commonly encountered in geometry and trigonometry problems, so understanding their properties is crucial for problem-solving and geometric calculations.