
If you are studying mechanics or physics, you have probably come across the topic of simple harmonic motion. Simple harmonic motion is a type of periodic motion where an object oscillates back and forth around a stable equilibrium position. This concept is widely used in various fields, such as engineering, astronomy, and music.
Understanding the principles of simple harmonic motion is key to solving problems related to this topic. One effective way to practice and test your knowledge is by working on worksheets. Simple harmonic motion worksheets provide a set of questions and problems that require you to apply the formulas and concepts you have learned.
In these worksheets, you will encounter different types of questions, including finding the period and frequency of oscillation, calculating the maximum displacement, determining the amplitude, and solving problems with springs and pendulums. By completing these worksheets, you can enhance your understanding of simple harmonic motion and improve your problem-solving skills.
If you are looking for simple harmonic motion worksheets with answers, you are in luck. Having access to the answers can be incredibly helpful in checking your work and identifying any mistakes you may have made. Additionally, seeing the correct solutions can provide you with valuable insights on how to approach similar problems in the future.
Whether you are a student studying for an exam, a teacher looking for practice materials, or simply someone interested in learning more about simple harmonic motion, using worksheets with answers can be a great resource to further your understanding of this fascinating topic.
Simple Harmonic Motion Worksheet with Answers
In the study of physics, simple harmonic motion (SHM) is a type of periodic motion in which an object oscillates back and forth around an equilibrium position, with a force that is directly proportional to its displacement from that position. SHM is commonly encountered in everyday life, such as the swinging of a pendulum or the oscillations of a mass-spring system.
A simple harmonic motion worksheet with answers is a helpful tool for students to practice and reinforce their understanding of SHM concepts. This worksheet typically consists of a series of questions and problems related to SHM, and includes detailed solutions or answers for reference.
One type of question that may be included in a simple harmonic motion worksheet is calculating the period or frequency of an oscillating system. Students are given the necessary information, such as the mass or length of a pendulum, and must use the appropriate equation to determine the period or frequency. This helps students become familiar with the mathematical relationships involved in SHM.
Another type of question that may be included in a simple harmonic motion worksheet is determining the maximum displacement or amplitude of an oscillating system. Students are provided with the necessary information, such as the equilibrium position or the maximum force applied, and must apply the appropriate formula to find the maximum displacement. This helps students understand the physical characteristics of SHM and how they relate to the equations used to describe it.
In addition to these quantitative questions, a simple harmonic motion worksheet may also include conceptual questions that require students to think critically and explain their reasoning. For example, students may be asked to explain why the period of a pendulum is independent of its amplitude, or to compare and contrast the motion of a mass-spring system with that of a pendulum. These types of questions help students develop a deeper understanding of SHM and how it applies to real-world phenomena.
Overall, a simple harmonic motion worksheet with answers is a valuable resource for students to practice and apply their knowledge of SHM. By providing a range of questions and problems, as well as detailed solutions, students can enhance their understanding of the key concepts and equations involved in SHM.
What is Simple Harmonic Motion?
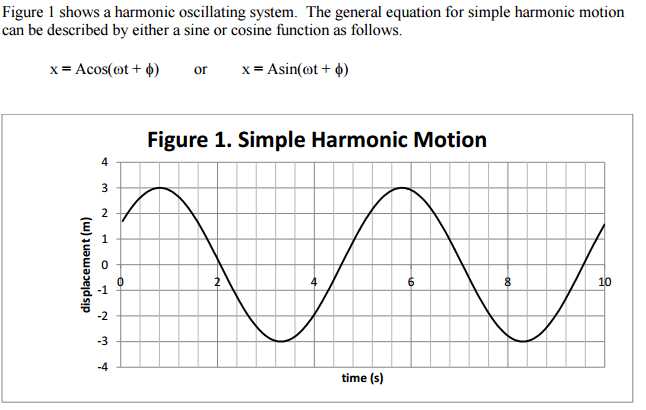
In physics, simple harmonic motion (SHM) is a type of periodic motion that occurs when an object oscillates back and forth around an equilibrium position. It is characterized by a restoring force that is directly proportional to the object’s displacement from the equilibrium position and acts in the opposite direction of the displacement.
Equilibrium position: The position where the net force acting on the object is zero, and the object is at rest.
When an object is in simple harmonic motion, it follows a sinusoidal pattern, moving back and forth along a single axis. This motion can be described mathematically using equations that represent the position, velocity, and acceleration of the object at any given time. The simplest form of simple harmonic motion is a mass-spring system, where a mass is attached to a spring and allowed to oscillate.
Period: The time taken for one complete cycle of motion.
Example: The motion of a pendulum swinging back and forth can be considered as simple harmonic motion as long as the angle of displacement is small enough for the approximation to be valid.
- In SHM, the maximum displacement of the object from the equilibrium position is called the amplitude.
- The frequency of the motion, which is the number of complete cycles per unit of time, is inversely proportional to the period of the motion.
Equations of Simple Harmonic Motion

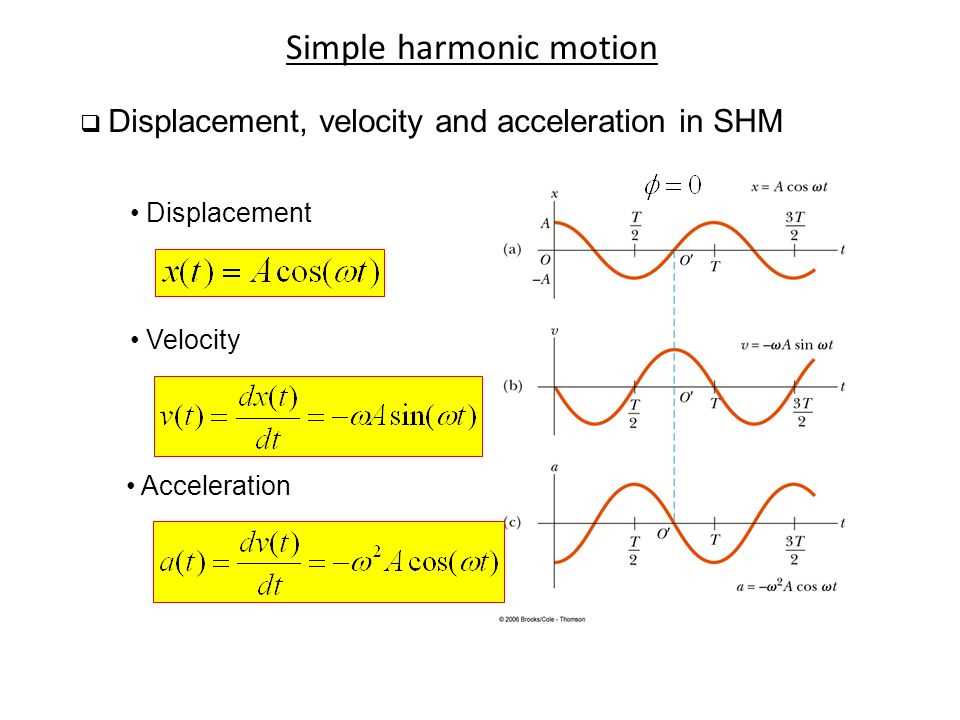
In simple harmonic motion, a mass attached to a spring oscillates back and forth, creating a repetitive pattern. This motion can be described using a set of equations that define the displacement, velocity, and acceleration of the mass at any given time.
The displacement of the mass from its equilibrium position can be described by the equation:
Δ x = Acos(2πft + φ)
Where Δ x is the displacement, A is the amplitude (maximum displacement), f is the frequency, t is the time, and φ is the phase constant.
The velocity of the mass can be calculated by taking the derivative of the displacement equation:
v = -2πAfsin(2πft + φ)
Where v is the velocity.
The acceleration of the mass can be calculated by taking the derivative of the velocity equation:
a = -4▂Afcos(2πft + φ)
Where a is the acceleration.
These equations provide a mathematical representation of the motion of a mass in simple harmonic motion and can be used to analyze and predict the behavior of systems exhibiting this type of motion.
Examples of Simple Harmonic Motion
Simple Harmonic Motion (SHM) is a type of periodic motion in which an object oscillates back and forth around an equilibrium position. This motion can be found in various objects and phenomena in our daily lives. Here are some examples of SHM:
- Pendulum: A pendulum is a classic example of SHM. It consists of a weight suspended from a pivot point, and when it is displaced from its equilibrium position and released, it swings back and forth in a regular pattern.
- Spring-Mass System: Another common example of SHM is a spring-mass system. When a mass is attached to a spring and pulled or pushed out of its equilibrium position, it undergoes simple harmonic motion as it moves back and forth. This can be observed in objects like a car’s suspension system or a diving board.
- Tuning Fork: A tuning fork is a musical instrument that produces a pure tone when struck. Its vibrations can be modeled as simple harmonic motion. When it is hit, the two prongs of the tuning fork oscillate back and forth, producing a sound with a specific frequency.
- Swinging Pendulum Clock: The swinging pendulum in a clock is also an example of SHM. As the pendulum swings back and forth, its motion is governed by the laws of simple harmonic motion, allowing the clock to keep accurate time.
- Musical Instruments: Many musical instruments, such as guitars, violins, and pianos, rely on the principles of simple harmonic motion to produce sound. The vibrations of strings or air columns in these instruments create the distinctive tones we hear when they are played.
These examples demonstrate the ubiquity of simple harmonic motion in our everyday lives. Understanding the principles behind SHM helps in various fields like physics, engineering, and music, allowing us to analyze and predict the behavior of oscillating systems.
Characteristics of Simple Harmonic Motion
Simple Harmonic Motion (SHM) is a type of periodic motion that can be observed in many different systems, such as oscillating springs, pendulums, and vibrating objects. It is characterized by a repeating pattern of motion in which the object or system moves back and forth around a stable equilibrium position.
There are several key characteristics of Simple Harmonic Motion:
- Frequency: The frequency of SHM is the number of complete oscillations or cycles that occur in a given time period. It is usually measured in hertz (Hz) and is inversely proportional to the period of the motion.
- Period: The period of SHM is the time it takes for one complete oscillation to occur. It is the reciprocal of the frequency and is often denoted by the symbol T.
- Amplitude: The amplitude of SHM is the maximum displacement or distance from the equilibrium position that the object or system reaches during its motion. It represents the maximum amount of energy that is present in the system.
- Uniform Motion: In SHM, the object or system moves with a constant velocity at the equilibrium position. This means that the net force acting on the object is zero, resulting in a uniform motion.
- Restoring Force: The restoring force in SHM is the force that acts on the object or system to bring it back towards the equilibrium position when it is displaced. It is proportional to the displacement and acts in the opposite direction to the displacement.
- Phase: The phase of SHM is a measure of the position of the object or system within one complete oscillation. It is often represented in terms of the angle or fraction of a complete cycle.
- Energy: SHM involves the transfer of potential energy to kinetic energy and back again. As the object or system oscillates, the potential energy is greatest at the extremes of the motion, while the kinetic energy is greatest at the equilibrium position.
By understanding and analyzing these characteristics, scientists and engineers can better predict and describe the behavior of systems that exhibit simple harmonic motion. This knowledge is essential in many fields, including physics, engineering, and even music.
Relationship between Simple Harmonic Motion and Waves

Simple harmonic motion (SHM) and waves are closely related phenomena that are governed by similar mathematical equations and principles. Understanding the relationship between SHM and waves is crucial in many areas of physics, including the study of vibrations, oscillations, and wave propagation.
In simple harmonic motion, an object oscillates back and forth along a straight line due to a restoring force that is proportional to its displacement from the equilibrium position. This motion can be described mathematically using sine or cosine functions, which are also used to describe waves. Both SHM and waves exhibit periodic behavior, where the motion or oscillation repeats itself over time.
A wave is defined as a disturbance or oscillation that travels through a medium, carrying energy from one place to another. Sound waves, water waves, and light waves are examples of waves that can be described using simple harmonic motion. In fact, all waves can be mathematically expressed as a superposition of simple harmonic oscillations with different frequencies and amplitudes, known as Fourier analysis.
When an object undergoes simple harmonic motion, it can create waves in a surrounding medium, such as air or water. These waves propagate outward from the source and can be observed as disturbances or oscillations in the medium. Similarly, waves can cause objects or particles in the medium to undergo simple harmonic motion as they pass through.
Overall, the relationship between simple harmonic motion and waves lies in the mathematical description of their behavior and the transfer of energy through oscillatory motion. By understanding the principles of SHM and waves, scientists and engineers can analyze and predict the behavior of various systems, from pendulums and springs to the propagation of sound or electromagnetic waves.
Energy in Simple Harmonic Motion
In simple harmonic motion, energy is constantly being exchanged between potential energy and kinetic energy. As an oscillating object moves back and forth, it reaches maximum displacement and maximum velocity at different points in its motion. This interchange of energy can be explained by understanding the concepts of potential energy and kinetic energy.
Potential energy is the energy an object possesses due to its position or configuration. In the case of simple harmonic motion, potential energy is maximum at the extreme points of the oscillation, where the object is furthest from its equilibrium position. As the object moves towards the equilibrium position, potential energy is converted into kinetic energy.
Kinetic energy is the energy of an object in motion. In simple harmonic motion, kinetic energy is maximum at the equilibrium position, where the object is moving with its maximum speed. As the object moves away from the equilibrium position, kinetic energy is converted back into potential energy.
This exchange of energy between potential and kinetic energy allows the oscillating object to continue its motion indefinitely, with the total mechanical energy remaining constant. The total mechanical energy is the sum of the potential energy and kinetic energy of the object at any given point in its motion.
Summary of Energy in Simple Harmonic Motion:
- Potential energy is maximum at the extreme points of the oscillation.
- Kinetic energy is maximum at the equilibrium position.
- As the object moves towards the equilibrium position, potential energy is converted into kinetic energy.
- As the object moves away from the equilibrium position, kinetic energy is converted back into potential energy.
- The total mechanical energy remains constant throughout the motion.
Understanding the interplay of potential and kinetic energy in simple harmonic motion is crucial in analyzing and predicting the behavior of oscillating systems in various fields, such as physics, engineering, and astronomy.