Test 6a AP Statistics is a comprehensive assessment that evaluates students’ understanding and application of statistical concepts. This test is designed to measure their proficiency in statistical analysis, data interpretation, and hypothesis testing.
The Test 6a AP Statistics covers a wide range of topics, including probability, sampling distributions, confidence intervals, and hypothesis testing. Students will be required to solve complex problems and demonstrate their ability to apply statistical methods to real-world scenarios.
One of the main objectives of the Test 6a AP Statistics is to assess students’ ability to organize and summarize data using appropriate graphical and numerical techniques. They will be expected to interpret these representations and draw meaningful conclusions from the data.
Furthermore, the test evaluates students’ understanding of sampling methods and the impact of sample size on the validity of statistical inferences. Students will need to identify the appropriate method for collecting data and determine the sample size required to achieve a desired level of precision.
In conclusion, the Test 6a AP Statistics is a rigorous examination that assesses students’ proficiency in statistical analysis and data interpretation. It tests their ability to apply statistical methods to real-world scenarios and draw meaningful conclusions from data. By successfully completing this test, students demonstrate their readiness for college-level statistics courses and their ability to apply statistical concepts in various fields.
Test 6a AP Statistics: An Overview of Topics and Concepts
Test 6a in AP Statistics covers a variety of topics and concepts that are important for understanding and analyzing statistical data. These topics include sampling and experimental design, probability, random variables, and sampling distributions.
One of the key components of this test is understanding sampling and experimental design. This involves knowing how to collect data in a way that is representative of the population being studied and minimizing bias. It also includes understanding different types of sampling methods, such as simple random sampling, stratified sampling, and cluster sampling.
Probability is another important concept that is tested in Test 6a. Students are expected to understand the basic principles of probability, such as calculating probabilities using counting rules and understanding the concept of independence. They should also be able to apply these principles to solve problems involving experiments with equally likely outcomes and conditional probability.
Random variables and their probability distributions are also covered in this test. Students should be able to identify and differentiate between discrete and continuous random variables, as well as understand the concept of expected value and variance. They should also be able to calculate probabilities and expected values for different types of distributions, such as the binomial and normal distributions.
Lastly, Test 6a covers sampling distributions, which involves understanding the concept of a sampling distribution and its relationship to the population distribution. Students should be able to calculate and interpret confidence intervals and understand the concept of hypothesis testing.
In summary, Test 6a in AP Statistics covers a range of topics and concepts essential for understanding and analyzing statistical data. These include sampling and experimental design, probability, random variables, and sampling distributions. It is important for students to have a strong grasp of these concepts in order to succeed on this test.
Understanding the Basics of Test 6a in AP Statistics
The Test 6a in AP Statistics is an important assessment that evaluates students’ understanding of various statistical concepts and their ability to apply them in problem-solving scenarios. This test covers a range of topics, including hypothesis testing, confidence intervals, and regression analysis.
One of the key components of Test 6a is hypothesis testing. Students are required to understand the concept of null and alternative hypotheses and how to perform hypothesis tests using different statistical tests, such as the z-test or t-test. They need to be able to interpret the results of these tests and make conclusions based on the evidence provided by the data.
Another important aspect of Test 6a is the concept of confidence intervals. Students should be able to calculate and interpret confidence intervals and understand the relationship between confidence level, sample size, and the width of the interval. They need to understand that a wider interval corresponds to a higher confidence level and a smaller sample size, while a narrower interval implies a lower confidence level and a larger sample size.
Regression analysis is also covered in Test 6a. Students should be familiar with the basic concepts of linear regression, such as the slope and intercept of the regression line, as well as the coefficient of determination (R-squared) and the standard error of the estimate. They should be able to interpret the results of regression analysis and make predictions based on the regression equation.
In conclusion, Test 6a in AP Statistics assesses students’ knowledge and skills in hypothesis testing, confidence intervals, and regression analysis. It is important for students to thoroughly understand these concepts and practice applying them in various scenarios in order to perform well on this test.
Exploring Descriptive Statistics in Test 6a AP Statistics
The Test 6a in AP Statistics is designed to assess students’ understanding of descriptive statistics. Descriptive statistics involves the organization, summarization, and interpretation of data. It provides a way to describe and understand the characteristics of a given dataset. In Test 6a, students will be asked to apply various techniques and methods to analyze and interpret data, including measures of central tendency, measures of variability, and graphical displays.
One of the key concepts in descriptive statistics is the measures of central tendency. This includes the mean, median, and mode. The mean is calculated by summing up all the values in the dataset and dividing the sum by the number of observations. It represents the average value of the dataset. The median is the middle value when the data is arranged in ascending or descending order. It provides a measure of the central value that is not influenced by extreme values. The mode is the value that occurs most frequently in the dataset.
Another important aspect of descriptive statistics is measures of variability. These measures describe the spread or dispersion of the data. The range is the difference between the maximum and minimum values in the dataset. It provides a simple measure of dispersion, but it is sensitive to extreme values. The standard deviation is a more robust measure of variability that takes into account all the values in the dataset. It measures the average deviation of values from the mean. The variance is the square of the standard deviation.
- In Test 6a, students may be asked to calculate and interpret these measures of central tendency and variability to compare different datasets or draw conclusions about a given dataset.
- Students may also be required to create and interpret graphical displays such as histograms, boxplots, or scatterplots to visualize and analyze data.
- Understanding and applying these descriptive statistics concepts is crucial for analyzing and interpreting data in various fields, including social sciences, business, and healthcare.
Overall, exploring descriptive statistics in Test 6a AP Statistics allows students to develop a deeper understanding of how to summarize and interpret data, providing them with valuable skills for future statistical analysis.
Analyzing Probability and Random Variables in Test 6a AP Statistics
Test 6a in AP Statistics focuses on analyzing probability and random variables, two fundamental concepts in the field of statistics. Probability is the likelihood or chance of an event occurring, while random variables are numerical variables that can take on different values based on chance.
One key aspect of analyzing probability is understanding the concepts of independent and dependent events. Independent events are events that do not influence each other, meaning that the occurrence of one event does not affect the probability of the other event happening. Dependent events, on the other hand, are events where the occurrence of one event influences the probability of the other event happening.
To analyze random variables, it is important to understand their probability distributions. A probability distribution describes the likelihood of various outcomes for a random variable. Two common types of probability distributions are discrete and continuous. Discrete random variables have a countable number of possible values, such as the number of heads obtained when flipping a coin. Continuous random variables, on the other hand, can take on any value within a given range, such as the height of individuals in a population.
When analyzing random variables, it is also important to be familiar with concepts such as expected value and variance. The expected value represents the average value of a random variable, while variance measures the spread or variability of the values that the random variable can take on.
In summary, Test 6a in AP Statistics focuses on analyzing probability and random variables. Understanding the concepts of independent and dependent events, as well as probability distributions, expected value, and variance, is crucial for successfully analyzing and interpreting data in statistics.
Examining Sampling Distributions in Test 6a AP Statistics
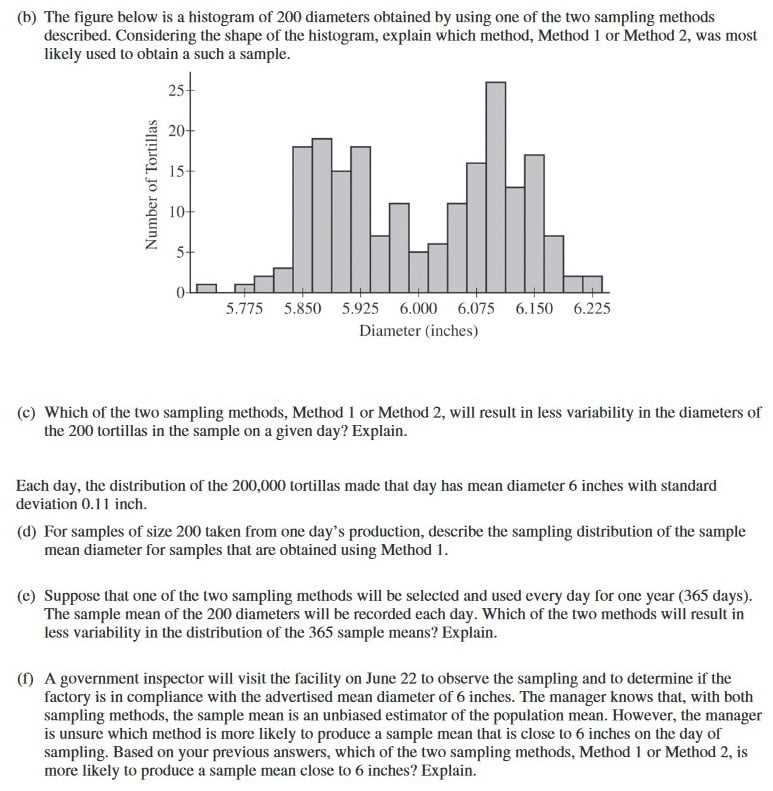
In Test 6a of AP Statistics, sampling distributions are a crucial topic that students need to understand. A sampling distribution is a theoretical distribution that shows the possible values of a statistic (such as the mean or proportion) based on different samples taken from a population. It helps us understand the variability and the behavior of the statistic across multiple samples.
One of the key concepts covered in Test 6a is the Central Limit Theorem. This theorem states that, regardless of the shape of the population distribution, the sampling distribution of the sample mean will approach a normal distribution as the sample size gets larger. This is true as long as the samples are randomly selected and the sample size is large enough (usually at least 30). This property of the Central Limit Theorem is especially useful in applications where the sample mean is of interest, such as estimating population parameters.
The test also explores the idea of standard error, which is the standard deviation of a sampling distribution. It measures the spread or variability of the sampling distribution. As the sample size increases, the standard error decreases, indicating that there is less variability in the estimates obtained from different samples. Standard error is an important concept for determining the precision of a sample statistic.
To better understand these concepts, students are often required to calculate and interpret sampling distributions in various scenarios. They need to be able to calculate the mean and standard deviation of a sampling distribution and interpret the results in the context of the problem. They also need to know how to use the information from a sampling distribution to make inferences about the population parameters or compare different samples.
Overall, understanding sampling distributions is crucial in AP Statistics as it allows students to make accurate and reliable inferences about the population based on sample data. It helps them understand the behavior of statistics and provides a foundation for hypothesis testing, confidence intervals, and other statistical techniques.
Investigating Confidence Intervals and Hypothesis Testing in Test 6a AP Statistics
In Test 6a of AP Statistics, students are challenged with investigating confidence intervals and hypothesis testing. These statistical concepts play a crucial role in understanding the reliability of data and drawing conclusions from sample data. Confidence intervals allow statisticians to estimate the population parameter within a certain range, while hypothesis testing helps determine whether a specific claim or hypothesis about the population is supported by the available data.
One of the main tasks in Test 6a is to calculate a confidence interval based on a sample mean and standard deviation. This involves using the t-distribution and considering the desired level of confidence, sample size, and standard deviation. By finding the margin of error and adding or subtracting it from the sample mean, students can construct an interval within which they can expect the true population mean to fall with a certain level of confidence. Understanding how to interpret and calculate confidence intervals is essential for drawing reliable conclusions from sample data.
Another important aspect of Test 6a is hypothesis testing. Students are confronted with hypothesized population parameters and are required to assess the evidence for or against these hypotheses using statistical methods. This involves calculating test statistics, determining p-values, and making decisions based on the level of significance. Whether it is a one-sample t-test, two-sample t-test, or a test for proportions, hypothesis testing allows students to make inferences about the population based on sample data and draw statistically valid conclusions.
Overall, Test 6a focuses on investigating confidence intervals and hypothesis testing, two fundamental concepts in AP Statistics. By mastering these concepts, students gain the ability to analyze data, draw accurate conclusions, and make informed decisions based on statistical evidence. This knowledge is vital for anyone working with data and seeking to make evidence-based claims or develop effective strategies.
Understanding Regression and Correlation in Test 6a AP Statistics
Regression and correlation are important concepts in the field of statistics, as they allow us to analyze the relationship between two variables and make predictions based on that relationship. In Test 6a of AP Statistics, students are expected to demonstrate their understanding of these concepts through various problems and scenarios.
Regression analysis involves determining the equation of a line that best represents the relationship between two variables. This equation is often referred to as the regression equation, and it can be used to predict the value of one variable based on the value of the other. In Test 6a, students may be asked to calculate the regression equation using given data points, or to interpret the slope and intercept of the equation in the context of the problem.
Correlation, on the other hand, measures the strength and direction of the linear relationship between two variables. It can be positive, indicating that as one variable increases, the other also increases, or negative, indicating that as one variable increases, the other decreases. In Test 6a, students may be asked to calculate the correlation coefficient using a given data set, or to interpret the meaning of the coefficient in relation to the problem scenario.
Overall, a strong understanding of regression and correlation is essential for any statistician or data analyst. It allows us to analyze and interpret the relationships between variables, make predictions, and draw conclusions from data. Test 6a of AP Statistics offers students the opportunity to apply this knowledge in a variety of problem-solving situations, further solidifying their comprehension of these important statistical concepts.