Quadratic functions and equations are an essential topic in mathematics that deals with finding solutions to equations with squared terms. In Chapter 9 of a textbook or study guide, you will typically find an answer key that provides the solutions to the problems or exercises presented throughout the chapter.
Understanding quadratic functions and equations is crucial as they have numerous real-world applications. From physics to finance, quadratic equations are used to model various phenomena and solve problems. Having the answer key to Chapter 9 allows students to check their work and verify if their solutions are correct.
The answer key provides step-by-step solutions to the problems, helping students understand the process of solving quadratic equations. It highlights the key steps and formulas involved, allowing learners to grasp the concept better. By referring to the answer key, students can identify any mistakes they made and learn from them.
Additionally, the answer key in Chapter 9 of a textbook serves as a valuable study resource for exams and assessments. It allows students to practice solving different types of quadratic equations and evaluate their progress. By working through the problems and comparing their solutions to the provided answers, students can build confidence in their abilities and improve their proficiency in quadratic functions and equations.
Chapter 9 Quadratic Functions and Equations Answer Key
Chapter 9 of the textbook focuses on quadratic functions and equations. This answer key provides a comprehensive overview of the chapter, helping students understand the concepts and solve problems effectively.
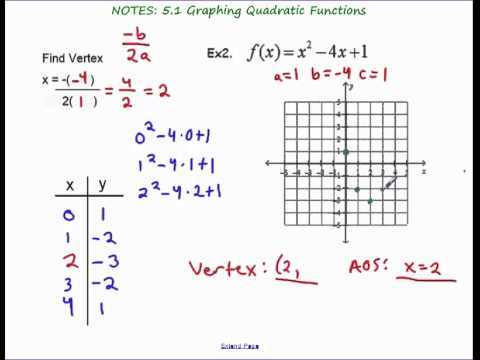
The answer key begins by introducing the basics of quadratic functions, including their form, graph, and key features such as the axis of symmetry and vertex. It explains how to find the vertex of a quadratic function using the formula, and provides examples to illustrate the process.
Next, the answer key discusses quadratic equations and highlights the different methods for solving them–factoring, completing the square, and using the quadratic formula. It demonstrates each method step-by-step and provides practice problems for students to reinforce their understanding.
The answer key also covers the concept of quadratic regression, which involves finding a quadratic function that best fits a set of data points. It explains how to use technology tools, such as graphing calculators or spreadsheet software, to perform a quadratic regression and determine the equation of the best-fit quadratic function.
Throughout the answer key, there are numerous examples and practice problems that cover a range of difficulty levels. This allows students to gradually build their skills and confidence in solving quadratic functions and equations. The answer key also includes explanations for common mistakes and offers tips on problem-solving strategies.
By using the Chapter 9 Quadratic Functions and Equations Answer Key, students can check their answers, understand their mistakes, and learn from them. It serves as a valuable tool for self-assessment and ensuring mastery of the concepts covered in this chapter.
Overview of Quadratic Functions and Equations
A quadratic function is a polynomial function of degree 2. It can be written in the form f(x) = ax^2 + bx + c, where a, b, and c are real numbers and a ≠ 0. Quadratic functions can be graphed as parabolas, which are symmetric about a vertical line called the axis of symmetry.
Quadratic equations are equations that can be written in the form ax^2 + bx + c = 0, where a, b, and c are real numbers and a ≠ 0. The solutions to quadratic equations are found by factoring, using the quadratic formula, completing the square, or graphing the equation and determining where the graph intersects the x-axis.
In order to graph a quadratic function, it is important to understand key features such as the vertex, axis of symmetry, and maximum or minimum value. The vertex of a parabola is the highest or lowest point on the graph, and it can be found using the formula x = -b/2a. The axis of symmetry is a vertical line that passes through the vertex and divides the parabola into two symmetric parts.
Quadratic functions and equations have various real-life applications, such as modeling the motion of projectiles, predicting the maximum or minimum value of a quantity, and solving optimization problems. Understanding quadratic functions and equations is essential in algebra and is a foundation for further mathematical concepts and applications.
Understanding the Standard Form of a Quadratic Equation

The standard form of a quadratic equation is written as ax^2 + bx + c = 0, where a, b, and c are constants. This form allows us to easily identify the coefficients and constant term in the equation.
One benefit of using the standard form is that it provides a clear representation of the quadratic equation and allows us to compare different equations. The coefficient a represents the coefficient of the quadratic term, b represents the coefficient of the linear term, and c is the constant term. By analyzing these coefficients, we can determine the behavior of the quadratic equation.
When graphed, quadratic equations in standard form can appear as parabolas, with the vertex representing the minimum or maximum point of the graph. The direction of the parabola and the position of the vertex can be determined by analyzing the values of a and b.
The standard form also allows us to easily solve quadratic equations. By setting the equation equal to zero, we can use various techniques such as factoring, completing the square, or using the quadratic formula to find the solutions. Solving the equation helps us determine the x-intercepts, which represent the points where the parabola intersects the x-axis.
In summary, understanding the standard form of a quadratic equation is essential for analyzing and solving quadratic equations. It provides valuable information about the coefficients, allows for easy comparison between equations, and helps us identify the behavior of the graph. By utilizing the standard form, we can efficiently solve quadratic equations and determine their key properties.
Solving Quadratic Equations by Factoring

One method of solving quadratic equations is through factoring. Factoring is the process of rewriting a quadratic equation as a product of two linear factors. By setting each factor equal to zero, we can find the values of the variable that satisfy the equation.
To factor a quadratic equation, we look for two binomials whose product equals the quadratic expression. We can use either the distributive property or the FOIL method to expand the product of the two binomials and check if it matches the original quadratic equation.
When factoring quadratic equations, we often encounter cases where the equation has common factors or a leading coefficient of 1. These simplifications make it easier to find the linear factors and solve for the variable. However, there may be cases where factoring is not possible, especially when the equation is not easily factorable or has complex roots.
Once we have factored the quadratic equation into linear factors, we set each factor equal to zero and solve for the variable. These solutions are called the roots or zeros of the quadratic equation. Factoring allows us to solve quadratic equations not only algebraically but also graphically, as the roots represent the x-intercepts of the quadratic function’s graph.
Overall, factoring is a powerful tool for solving quadratic equations, providing a systematic approach to finding the roots of the equation. It is important to understand the process of factoring and practice applying it to different quadratic equations in order to become proficient in solving them.
Completing the Square to Solve Quadratic Equations

In the study of quadratic functions and equations, one important method of solving quadratic equations is called “completing the square”. This method involves transforming a quadratic equation into a perfect square trinomial, which can then be easily factored or solved using square roots.
To complete the square, we take a quadratic equation in the form of ax^2 + bx + c = 0 and manipulate it to be in the form of (x – h)^2 = k. The constant term, c, is moved to the other side of the equation, and then we add and subtract (b/2a)^2 to both sides to create a perfect square trinomial.
Once the quadratic equation is in the form of (x – h)^2 = k, we can easily solve for x by taking the square root of both sides and solving for x – h. We can then find the two possible values of x by adding and subtracting h to both sides.
Completing the square is a powerful tool for solving quadratic equations because it guarantees that the equation will have real solutions. It is especially useful when the coefficient of x^2 is not equal to 1, as it allows us to transform the equation into a more manageable form.
In conclusion, completing the square is an effective method for solving quadratic equations. By manipulating the equation into a perfect square trinomial, we can easily solve for x and find the real solutions to the equation. This method is particularly helpful when dealing with quadratic equations that have non-unity coefficients, allowing us to simplify the equation and find its solutions.
Quadratic Formula: A Powerful Tool for Solving Equations
The quadratic formula is an essential tool in mathematics for solving equations of the form ax^2 + bx + c = 0, where a, b, and c are constants. This formula allows us to find the values of x that satisfy the equation, also known as the roots or solutions.
The quadratic formula is derived from completing the square method and provides a reliable and efficient way to find solutions for quadratic equations. It is represented as:
x = ( -b ± √(b^2 – 4ac) ) / 2a
Here, ± denotes both the positive and negative values of the square root. To use the quadratic formula, we substitute the values of a, b, and c into the equation and solve for x. The discriminant (b^2 – 4ac) under the square root determines the nature of the solutions.
There are three possible scenarios based on the discriminant:
- If the discriminant is positive, we have two distinct real roots.
- If the discriminant is zero, we have one real root with a multiplicity of 2.
- If the discriminant is negative, the equation has two complex roots (conjugate pairs) in the form of a + bi and a – bi.
The quadratic formula is a powerful tool because it can handle any quadratic equation, even when the equation does not factor easily. It is a fundamental concept in algebra and is extensively used in various fields such as physics, engineering, and computer science, where quadratic equations frequently arise.
By utilizing the quadratic formula, mathematicians and scientists can efficiently solve complex equations, analyze mathematical models, and make accurate predictions. It provides a systematic approach to find solutions and helps in understanding the behavior of quadratic functions and their graphs.
Graphing Quadratic Functions: Parabolas and Their Properties
A quadratic function is a polynomial function of degree 2, which can be represented by a parabola when graphed. The graph of a quadratic function is a U-shaped curve called a parabola. Understanding the properties of a parabola can help us interpret and analyze quadratic functions.
One important property of a parabola is its vertex. The vertex is the point on the parabola that is either the highest or the lowest point, depending on whether the parabola opens upward or downward. The coordinates of the vertex can be determined using the formulas x = -b/2a and y = f(x), where a, b, and c are the coefficients of the quadratic function in standard form.
The axis of symmetry is another important property of a parabola. It is a vertical line that passes through the vertex and divides the parabola into two symmetric halves. The equation of the axis of symmetry can be determined by setting x = -b/2a.
A parabola can open upward or downward, depending on the sign of the coefficient a. If a is positive, the parabola opens upward, and if a is negative, the parabola opens downward. The value of a also determines the width of the parabola. A larger absolute value of a results in a narrower parabola, while a smaller absolute value of a results in a wider parabola.
Quadratic functions also have a y-intercept, which is the point where the graph intersects the y-axis. The equation of a quadratic function in standard form can be used to determine the y-intercept by setting x = 0.
By understanding and analyzing the properties of parabolas, we can effectively graph and interpret quadratic functions. The vertex, axis of symmetry, direction of opening, and y-intercept are all key components to consider when exploring quadratic functions and their graphs.
Applications of Quadratic Functions in Real Life
Quadratic functions, which are second-degree polynomial functions, can be found in various real-life applications. One common application of quadratic functions is in the field of physics, particularly in the study of motion. The motion of objects in gravity is often described by quadratic equations. For example, when an object is thrown into the air, its height can be modeled using a quadratic function. Knowing the height of an object at different times can help determine its speed, acceleration, and other important parameters.
Another area where quadratic functions are used is in economics. In finance, quadratic functions can be used to model revenue, costs, and profit. For example, a company may use a quadratic function to determine the price at which it can maximize its profit. By finding the vertex of the quadratic function, which represents the maximum point, the company can set the optimal price to maximize its earnings.
Quadratic functions also find applications in engineering and architecture. Engineers often use quadratic functions to model the behavior of various structures, such as bridges and buildings, under different loads and conditions. By analyzing the quadratic function, engineers can determine the stability and strength of the structure. Architects can also use quadratic functions to design curves and shapes that are aesthetically pleasing, such as arches and domes.
In summary, quadratic functions are widely used in various fields to model and analyze real-life situations. Whether it is predicting the motion of objects, optimizing profit in economics, or designing structures in engineering, understanding and applying quadratic functions is essential for solving real-world problems.