In the field of mathematics, radicals and exponents are important concepts that are widely used in various calculations and problem-solving. They provide a way to simplify and manipulate expressions involving powers and roots. In the 5 11 unit test on radicals and exponents, students will be assessed on their understanding and application of these mathematical operations.
The test will cover topics such as simplifying expressions containing radicals, solving equations with exponents, and evaluating expressions involving powers and roots. Students will be required to demonstrate their knowledge of the properties and rules associated with radicals and exponents, as well as their ability to apply them in problem-solving situations.
By mastering the concepts and skills tested in this unit, students will develop a solid foundation in working with radicals and exponents, which will be beneficial in more advanced topics in mathematics and other related fields. It is important for students to practice and reinforce their understanding of these concepts through exercises and problem-solving activities.
Overall, the 5 11 unit test on radicals and exponents serves as an assessment of students’ ability to work with and understand these important mathematical operations. It provides an opportunity for students to demonstrate their proficiency in simplifying expressions, solving equations, and evaluating numerical expressions involving powers and roots. By successfully completing this unit test, students will have a strong foundation in working with radicals and exponents, setting them up for success in future mathematical endeavors.
What are radicals and exponents?
Radicands and exponents are key concepts in mathematics, specifically in the field of algebra. Radicals, also known as square roots, are mathematical expressions that represent the principal square root of a number. They are denoted by the radical symbol (√) followed by the number or expression inside it. For example, √9 represents the square root of 9, which is 3.
Exponents, on the other hand, involve raising a number to a power. They are represented by a superscript number written above and to the right of the base number. For instance, 5³ represents 5 raised to the power of 3, which equals 125. Exponents indicate how many times the base number is multiplied by itself.
Both radicals and exponents have important applications in various areas of mathematics and everyday life. They are used to simplify complex mathematical expressions, solve equations, and analyze data. Understanding these concepts is crucial for solving problems involving algebraic equations, quadratic functions, and exponential growth or decay.
It is also worth noting that radicals and exponents are interconnected. Taking the square root of a number is equivalent to raising it to the power of 1/2. Similarly, raising a number to the power of 1/n, where n is an integer, is equivalent to taking the nth root of the number.
In conclusion, radicals and exponents play a significant role in algebra and mathematics as a whole. They provide a means to manipulate and simplify numerical expressions, allowing for more efficient problem-solving and analysis.
Understanding the concept of radicals

The concept of radicals is an important part of mathematics that involves the manipulation of square roots. A radical is a symbol that represents a square root, and it is denoted by the radical symbol (√). It is used to express the inverse operation of squaring a number, and allows us to solve equations, simplify expressions, and solve various mathematical problems.
At its core, a radical represents the principal square root of a number. The principal square root is the positive square root of a number. For example, the principal square root of 25 is 5, as 5 × 5 = 25. However, there can also be a negative square root, which is denoted by adding a negative sign in front of the radical symbol (√). So, the negative square root of 25 is -5.
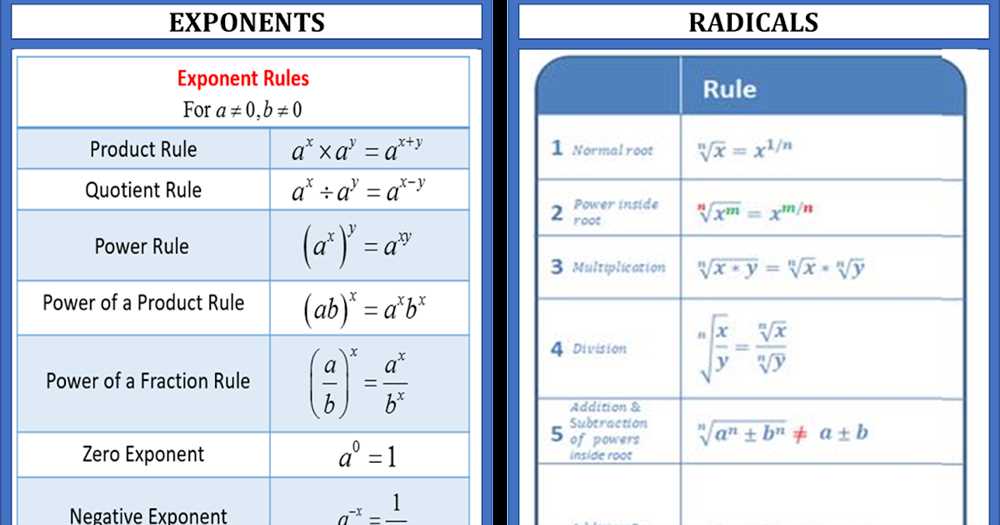
When dealing with radicals, it is important to understand the properties and rules associated with them. One important property is the product rule, which states that the square root of a product is equal to the product of the square roots of each individual factor. Another important rule is the quotient rule, which states that the square root of a quotient is equal to the quotient of the square roots of the numerator and denominator.
In addition, there are various techniques for simplifying radicals, such as factoring the number inside the radical or using rationalizing denominators. Simplifying radicals helps make expressions easier to work with and solve. It involves finding perfect square factors and simplifying them to their square root form.
Overall, understanding radicals is essential for working with advanced mathematical concepts. By mastering the concept of radicals, one can solve equations involving square roots, simplify expressions, and apply these skills to various real-life applications, such as in engineering, physics, and computer science.
Exploring the concept of exponents
In mathematics, exponents are a fundamental concept that helps us understand how numbers can be multiplied repeatedly. An exponent, also known as a power, is a small number written above and to the right of a base number, indicating the number of times the base should be multiplied by itself. For example, in the expression 53, the base is 5 and the exponent is 3. This means that 5 should be multiplied by itself three times: 5 x 5 x 5 = 125. Exponents allow us to simplify and express large numbers more efficiently.
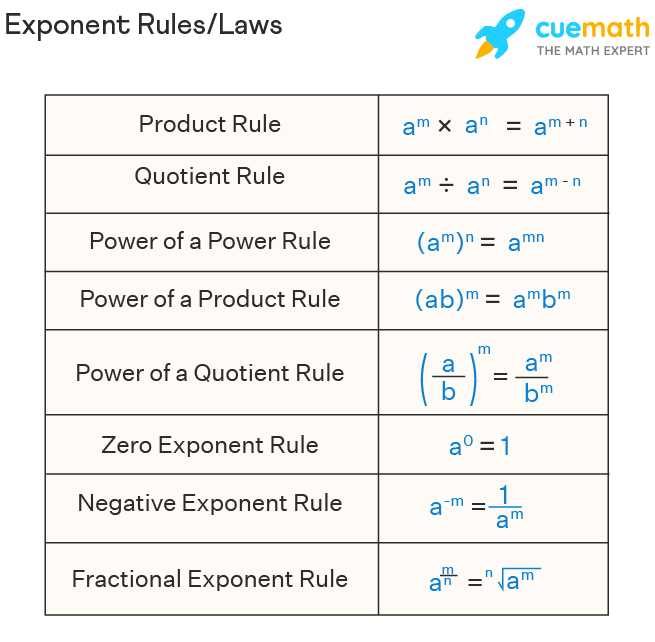
Exponents have several important properties that make calculations more manageable. One property is the power of a power rule, which states that when a base is raised to an exponent, and that result is raised to another exponent, the two exponents can be multiplied together. For instance, (23)2 is equal to 26, since 3 x 2 = 6. Another property is the product of powers rule, which states that when multiplying two numbers with the same base but different exponents, we can add the exponents together. For example, 43 x 42 can be simplified to 45, as 3 + 2 = 5.
Understanding exponents is crucial in various fields, including physics, engineering, and finance. In physics, exponents help us calculate values such as distance, time, and energy. In engineering, exponents are used to express numbers in scientific notation, making it easier to work with very large or small quantities. In finance, exponents are involved in compound interest calculations, which determine the growth of investments over time. By exploring and mastering the concept of exponents, we gain a powerful tool to solve complex problems and understand the world around us.
Key phrases:
- fundamental concept
- base number
- power
- multiply repeatedly
- power of a power rule
- product of powers rule
- simplify
- large numbers
- efficiently
- physics
- engineering
- finance
- scientific notation
- compound interest
- complex problems
Simplifying radical expressions

Radical expressions involve the use of square roots, cube roots, or any other root. Simplifying these expressions involves reducing them to their simplest form by removing any perfect square factors or perfect cube factors. Simplification allows us to work with the expressions more easily and evaluate them accurately.
When simplifying radical expressions, we follow specific steps. First, we identify perfect square factors or perfect cube factors within the expression. These are factors that can be simplified further. Next, we apply the corresponding exponent to each perfect square factor or perfect cube factor to simplify them. Finally, we combine like terms and rewrite the expression in its simplest form by removing any unnecessary radicals.
For example, let’s simplify the expression √(20) + 2√(5). We begin by identifying the perfect square factors within the expression, which in this case is 4. Applying the exponent of 2 to 4 gives us 2. Next, we combine the simplified factors and rewrite the expression as 2√(5) + 2√(5). Finally, we combine like terms to get the simplest form of the expression, which is 4√(5).
It’s important to note that simplifying radical expressions helps us in various mathematical calculations, such as solving equations, graphing functions, and performing operations involving radicals. By simplifying these expressions, we make the calculations simpler and more accurate, allowing us to better understand and analyze mathematical concepts.
Basic rules for simplifying radicals
When working with radicals, there are several basic rules that can help simplify and solve equations involving these mathematical expressions.
Rule 1: Simplifying square roots
When simplifying square roots, look for perfect square factors inside the radical. For example, the square root of 36 can be simplified as √(6 × 6) = 6.
Rule 2: Adding and subtracting radicals
When adding or subtracting radicals with the same index (such as square roots), the radicals can be combined if they have the same radicand. For example, √5 + √5 = 2√5.
Note: Only like radicals (same index and radicand) can be added or subtracted.
Rule 3: Multiplying and dividing radicals
When multiplying or dividing radicals, the radicands can be multiplied or divided together. For example, √3 × √4 = √(3 × 4) = √12.
When dividing radicals, the radicand of the denominator can be multiplied by the conjugate of the denominator to rationalize the denominator. For example, √5 / √3 = (√5 × √3) / (√3 × √3) = √15 / 3.
Rule 4: Simplifying higher index radicals

For radicals with an index greater than 2, the same rules as above apply, but the multiplication and division steps may involve raising the numbers inside the radical to a power. For example, ∛(2 × 4) = ∛(2^3 × 4^3) = ∛(8 × 64) = ∛(512) = 8.
By following these basic rules, simplifying radicals can become easier and more manageable, enabling you to solve equations involving these mathematical expressions.
Examples of simplifying radical expressions
Radical expressions involve the use of square roots or other roots to represent numbers. Simplifying these expressions involves finding the simplest form of the expression. Here are a few examples of how to simplify radical expressions:
Example 1:
Given the expression √12, we can simplify it by finding the largest perfect square that divides evenly into 12. We know that 4 is a perfect square that divides evenly into 12, so we can rewrite the expression as 2√3.
Example 2:
Let’s simplify the expression √27. We can find the largest perfect square that divides evenly into 27, which is 9. Thus, the expression becomes 3√3.
Example 3:
If we have an expression like √8, we need to find the largest perfect square that divides evenly into 8. In this case, it is 4. So, the expression simplifies to 2√2.
Example 4:
Consider the expression √18. We can find the largest perfect square that divides evenly into 18, which is 9. Thus, the expression simplifies to 3√2.
- To summarize:
- √12 simplifies to 2√3.
- √27 simplifies to 3√3.
- √8 simplifies to 2√2.
- √18 simplifies to 3√2.
By understanding the process of finding the largest perfect square that divides into a given number, we can simplify radical expressions and make them easier to work with in mathematical calculations.
Adding and Subtracting Radical Expressions
Radical expressions involve the use of square roots and other roots of numbers. When adding or subtracting radical expressions, it is important to simplify the expressions first before performing the operation.
To add or subtract radical expressions, first, identify the like terms. Like terms are those that have the same radicand, or the expression under the radical. For example, 2√3 and 4√3 are like terms because they both have a radicand of 3. On the other hand, 2√3 and 5√2 are not like terms because their radicands are different.
Once the like terms have been identified, you can add or subtract them by combining their coefficients. The coefficients are the numbers in front of the radical symbol. For example, in the expression 3√5 + 2√5, the like terms are 3√5 and 2√5, with coefficients of 3 and 2 respectively. Adding the coefficients gives a final result of 5√5.
If the radical expressions cannot be simplified or the radicands are not the same, you cannot add or subtract them directly. In such cases, you may need to use other algebraic techniques such as factoring or rationalizing the denominator to simplify the expressions and make them like terms.
It is important to note that when adding or subtracting radical expressions, you can only combine like terms. The radical symbols and the radicands should remain the same. Paying attention to these details will ensure that you correctly add or subtract radical expressions and simplify them as much as possible.
Steps for Adding and Subtracting Radical Expressions
Adding and subtracting radical expressions can be a complex process, but by following a few steps, you can simplify the process and achieve accurate results. Here are the steps to follow:
Step 1: Simplify the radicals. Before adding or subtracting radical expressions, simplify each individual radical expression as much as possible. Factor out any perfect squares or cubes and simplify any like terms under the radicals.
Step 2: Determine the common denominator. Just like with fractions, you need a common denominator in order to add or subtract radical expressions. To find the common denominator, identify the factors present in both denominators and multiply them together. This will ensure that all the expressions have the same radical factor.
Step 3: Add or subtract the radical expressions. Once you have determined the common denominator, you can add or subtract the simplified radical expressions. Treat the expressions as you would treat algebraic expressions with like terms. Add or subtract the coefficients outside the radical and keep the radical factor the same.
Step 4: Simplify the resulting expression. After adding or subtracting the radical expressions, simplify the resulting expression further if possible. Combine any like terms outside the radical and simplify any remaining radicals as much as possible by factoring out perfect squares or cubes.
By following these steps, you can ensure that you accurately add or subtract radical expressions and obtain simplified results. Remember to check your final answer to ensure it matches the original problem and that there are no further simplifications possible.