
When it comes to geometry, finding unknown angle measures is a common task. One type of angle relationship that often comes up is supplementary angles. Two angles are considered supplementary if the sum of their measures is 180 degrees. In this article, we will explore some examples of finding unknown angle measures using the concept of supplementary angles.
To find unknown angle measures in a pair of supplementary angles, we can use the fact that the sum of their measures is 180 degrees. This means that if we know the measure of one angle, we can easily find the measure of the other angle by subtracting the known measure from 180. This concept allows us to solve for the unknown angles in a variety of situations.
The key to finding unknown angle measures using supplementary angles is to set up an equation. Let’s say we have two supplementary angles, angle A and angle B. If we know that angle A measures 40 degrees, we can set up the equation: 40 + x = 180, where x represents the measure of angle B. By solving the equation, we find that angle B measures 140 degrees. This technique can be applied to any pair of supplementary angles.
Finding Unknown Angle Measures: Supplementary Angles 5 Answer Key
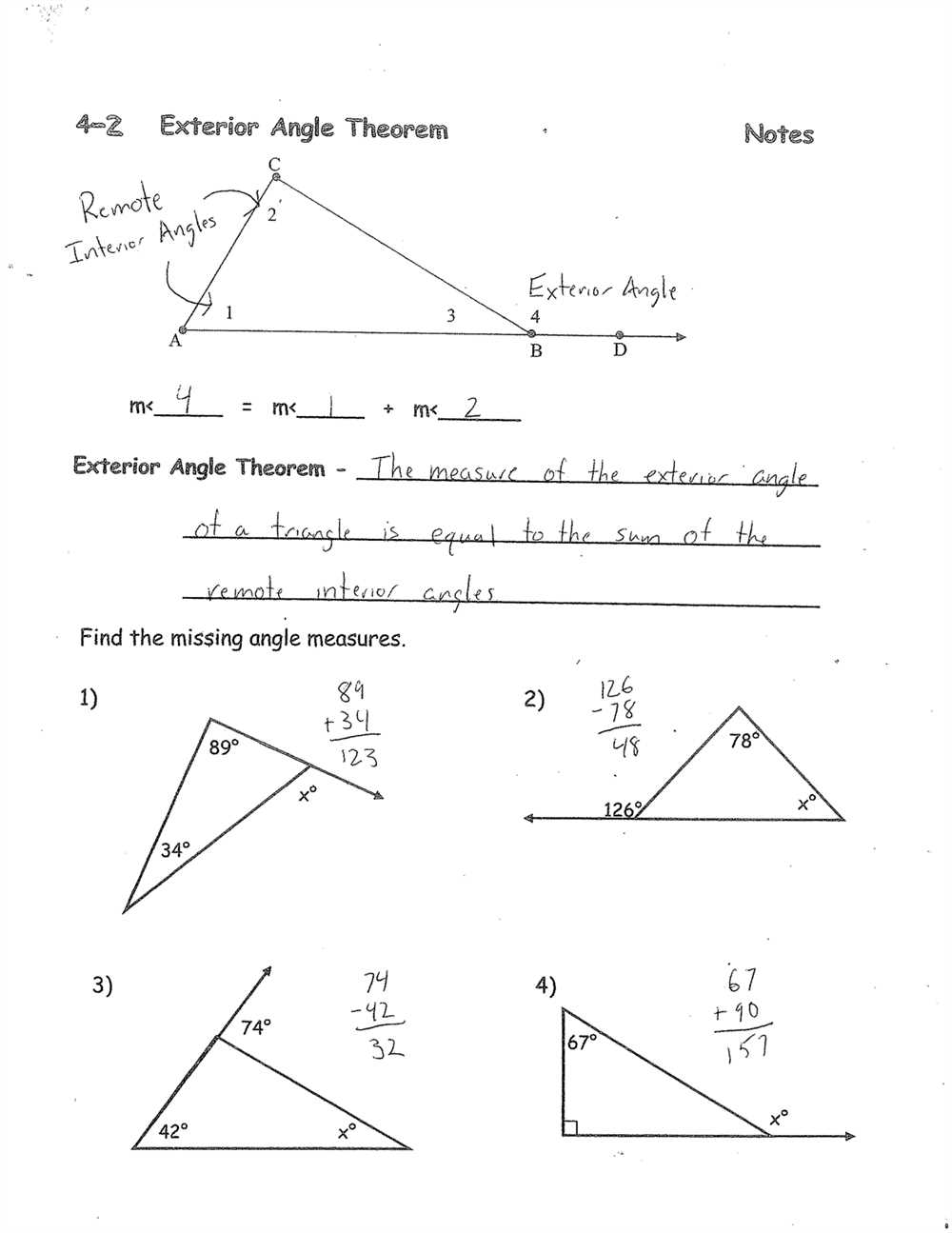
In geometry, supplementary angles are two angles that add up to 180 degrees. Finding unknown angle measures involving supplementary angles requires understanding the relationship between the given angles.
The answer key for the problem set “Supplementary Angles 5” is as follows:
- Problem 1: Angle 1 = 100 degrees
- Problem 2: Angle 1 = 90 degrees
- Problem 3: Angle 1 = 50 degrees
- Problem 4: Angle 1 = 40 degrees
- Problem 5: Angle 1 = 115 degrees
To find the unknown angle measure, you can subtract the given angle from 180 degrees. For example, in problem 1, if Angle 2 is given as 80 degrees, you subtract 80 from 180 to find that Angle 1 is 100 degrees. This is because Angles 1 and 2 are supplementary, meaning they add up to 180 degrees.
It is important to remember that the sum of the measures of supplementary angles is always 180 degrees. By using this key concept and subtracting the given angle from 180, you can find the unknown angle measure in any problem involving supplementary angles.
What are Supplementary Angles?
Supplementary angles are two angles whose measures add up to 180 degrees. In other words, they are a pair of angles that form a straight line when placed together. Each angle in a pair of supplementary angles is called a supplement of the other angle.
Supplementary angles can be found in various geometric shapes and situations. For example, in a triangle, if one angle measures 60 degrees, the other two angles must be supplementary and add up to 120 degrees. Similarly, in a quadrilateral, opposite angles are always supplementary.
Supplementary angles are important in geometry and can be used to solve various problems. By knowing the measure of one angle in a pair of supplementary angles, we can easily find the measure of the other angle by subtracting the given measure from 180 degrees. This property is used in finding unknown angle measures and solving equations involving angles.
To summarize, supplementary angles are a pair of angles whose measures add up to 180 degrees. They can be found in various geometric shapes and are useful in solving angle-related problems. Understanding the concept of supplementary angles helps in analyzing and manipulating angles in different contexts.
Understanding the Concept of Unknown Angle Measures
When it comes to geometry, understanding the concept of unknown angle measures is essential. In many geometric problems, angles are often given as variables, and the task is to find their values. This concept is particularly crucial when dealing with supplementary angles, which are two angles that add up to 180 degrees. By determining the unknown angle measures in supplementary angles, we can solve various geometric problems and gain a deeper understanding of the relationships between angles.
One approach to finding unknown angle measures in supplementary angles is to use the properties of angles. For example, if we have two supplementary angles and one angle measure is given (let’s say, 120 degrees), we can subtract it from 180 to find the measure of the unknown angle. In this case, the unknown angle would be 180 – 120 = 60 degrees. This method allows us to solve for the unknown angle measure in a straightforward manner.
Another approach to finding unknown angle measures involves using algebraic equations. By assigning a variable to the unknown angle measure and setting up an equation based on the given information, we can solve for the unknown variable. For instance, if we have two supplementary angles and one angle measure is twice the value of the other angle measure, we can set up the equation 2x + x = 180, where x represents the smaller angle measure. Solving this equation, we find that x = 60 degrees, and the unknown angle measure is 2x = 120 degrees.
Understanding the concept of unknown angle measures in supplementary angles is crucial in geometry, as it allows us to solve a wide range of geometric problems. Whether by using the properties of angles or setting up algebraic equations, finding unknown angle measures helps us uncover the relationships and connections between angles in different geometric contexts.
Why is it Important to Find Unknown Angle Measures?
Finding unknown angle measures is important in geometry because it allows us to understand and analyze the relationships between different angles and shapes. By determining the value of an unknown angle, we can solve geometrical problems, prove theorems, and make accurate measurements in real-life situations.
One of the key reasons why finding unknown angle measures is important is that it helps us solve problems involving supplementary angles. Supplementary angles are pairs of angles that add up to 180 degrees. By identifying and calculating the measures of unknown angles in a pair of supplementary angles, we can determine the missing angle and use it to solve various geometry problems.
Being able to find unknown angle measures also enables us to prove geometric theorems. In geometry, theorems are used to explain and prove mathematical statements. By determining the measures of unknown angles in a given figure or shape, we can apply theorems and make logical deductions to prove certain properties or relationships.
In addition to its theoretical importance, finding unknown angle measures has practical applications in real-life situations. For example, architects and engineers use angle measures to design and construct buildings, bridges, and other structures. By accurately determining unknown angles, they can ensure the stability and structural integrity of their designs.
In summary, finding unknown angle measures is important because it allows us to solve geometrical problems, prove theorems, and make accurate measurements in both theoretical and practical contexts. By understanding the relationships between angles and shapes, we can apply this knowledge to various mathematical and real-life situations.
Tips and Strategies for Finding Unknown Angle Measures
Finding unknown angle measures can be a challenging task, but with the right strategies, it can become easier and more manageable. Here are some tips to help you find unknown angle measures:
- Identify the Known Angles: Before you can find an unknown angle measure, it is important to identify the angles that are already known. This information will be crucial in determining the relationships between angles.
- Use Supplementary Angles: One strategy for finding unknown angle measures is to use the concept of supplementary angles. If two angles are supplementary, their measures add up to 180 degrees. By knowing the measure of one angle, you can subtract it from 180 degrees to find the measure of the unknown angle.
- Apply the Angle Sum Theorem: The Angle Sum Theorem states that the sum of the interior angles of a triangle is always 180 degrees. By knowing the measures of two angles in a triangle, you can subtract their sum from 180 degrees to find the measure of the third angle.
- Use Vertical Angles: Vertical angles are formed when two lines intersect. They are always congruent, which means they have the same measure. If you know the measure of one vertical angle, you can use it to find the measure of the other unknown angle.
- Apply the Angle Addition Postulate: The Angle Addition Postulate states that the measure of an angle formed by two adjacent angles is equal to the sum of their measures. By knowing the measures of the adjacent angles, you can add them together to find the measure of the unknown angle.
These tips and strategies can help you find unknown angle measures in different types of geometric problems. Remember to carefully analyze the given information and apply the appropriate concepts and theorems to solve the problem effectively.
Step-by-Step Guide to Finding Unknown Angle Measures for Supplementary Angles
In geometry, two angles are considered supplementary if the sum of their measures is equal to 180 degrees. Finding the measure of unknown angles when given supplementary angles is an important skill to have and can be easily done by following these step-by-step instructions.
Step 1: Identify the Supplementary Angles
Begin by identifying the pair of angles that are said to be supplementary. This can be indicated in the problem statement or visually represented in a diagram.
Step 2: Set up an Equation
Assign variables to the measures of the unknown angles. For example, let angle A be x and angle B be y. Since the angles are supplementary, their sum is 180 degrees, so the equation can be written as x + y = 180.
Step 3: Solve the Equation
Solve the equation to find the value of the unknown angle. This can be done by isolating one of the variables and substituting it back into the equation to solve for the other variable.
- If angle A is known to be 100 degrees, substitute x = 100 into the equation: 100 + y = 180.
- Then, solve for y: y = 180 – 100 = 80 degrees.
- Therefore, angle B measures 80 degrees.
Step 4: Check Your Answer
Check the solution by substituting the values back into the original equation. For example, 100 + 80 = 180, which verifies that the angles are indeed supplementary and that the measures are correct.
By following these steps, you can easily find the unknown angle measures for supplementary angles. This skill is essential in geometry problems involving angles and can be applied in various mathematical and real-life situations.
Common Challenges and Mistakes in Finding Unknown Angle Measures
In the process of finding unknown angle measures, there are several common challenges and mistakes that students often encounter. One of the most common challenges is understanding the concept of supplementary angles. Supplementary angles are two angles that add up to 180 degrees. Students may struggle with identifying pairs of angles that are supplementary, especially when they are given multiple angles to work with.
One mistake that students often make is failing to correctly identify the relationships between angles in a given figure. For example, they may mistakenly assume that two angles are supplementary when they are actually complementary or not related at all. This mistake can lead to incorrect calculations and inaccurate results.
Another challenge is correctly applying the angle measurements and properties of parallel lines. When working with parallel lines, there are various angle relationships to consider, such as corresponding angles, alternate interior angles, and alternate exterior angles. Students may struggle with identifying these angle relationships and applying them correctly to find unknown angle measures.
One common mistake that students make is using the wrong formula or equation to find an unknown angle measure. There are different formulas and equations that can be used, depending on the given information and the angle relationships involved. Using the wrong formula can result in incorrect calculations and an incorrect solution.
Lastly, students may struggle with correctly applying algebraic reasoning to solve for unknown angle measures. In some cases, students may need to set up and solve equations to find the value of an unknown angle. This requires a solid understanding of algebraic concepts and the ability to manipulate equations. Making mistakes in the algebraic reasoning process can lead to incorrect solutions.
In order to overcome these challenges and avoid common mistakes, it is important for students to practice identifying angle relationships, understand the properties of parallel lines, and review the appropriate formulas and equations for finding unknown angle measures. With practice and a solid understanding of these concepts, students can improve their ability to find unknown angle measures accurately and efficiently.
Supplementary Angles 5 Answer Key: Examples and Solutions
In geometry, supplementary angles are two angles that add up to 180 degrees. Finding the measures of unknown angles in a pair of supplementary angles can be challenging, but with practice, it becomes easier. The Supplementary Angles 5 Answer Key provides examples and solutions to help students understand and solve problems involving supplementary angles.
One example from the answer key is as follows: Given that angle ABC measures 120 degrees, find the measure of its supplementary angle. The solution is to subtract the measure of angle ABC from 180 degrees, giving us 60 degrees. Therefore, the supplementary angle measures 60 degrees.
Another example is: If angle DEF measures 90 degrees, find the measure of its supplementary angle. The solution is to subtract the measure of angle DEF from 180 degrees, which gives us 90 degrees. Therefore, the supplementary angle measures 90 degrees.
The Supplementary Angles 5 Answer Key also includes additional examples and solutions that cover a range of angle measures and scenarios. These examples help students practice finding unknown angles in pairs of supplementary angles and reinforce important concepts and techniques.
By studying the examples and solutions in the Supplementary Angles 5 Answer Key, students can improve their understanding of supplementary angles and develop their problem-solving skills. This key can be a valuable resource for both teachers and students, providing clear explanations and step-by-step solutions to assist with learning and comprehension.