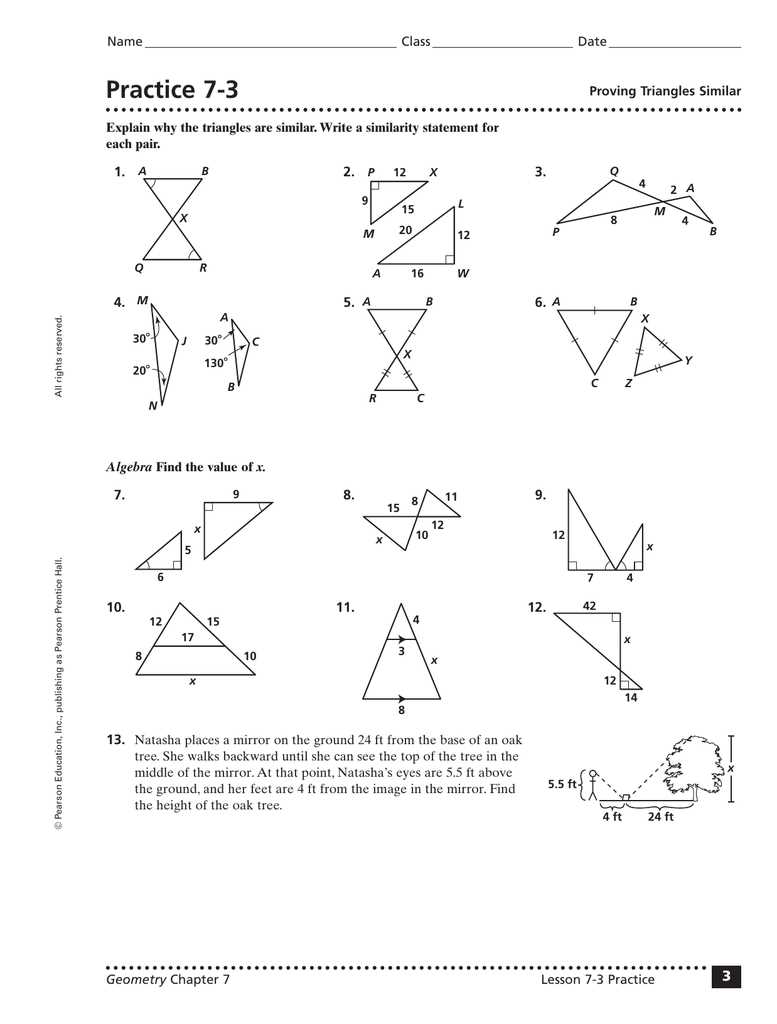
In geometry, proportions are an important concept to understand, especially when it comes to triangles. Proportions allow us to compare the lengths of different sides of a triangle and find missing lengths. One common way to work with proportions in triangles is through the use of worksheets.
The 7 5 proportions in triangles worksheet is designed to help students practice solving for missing side lengths in triangles using proportions. This worksheet includes a variety of triangle problems, such as finding missing sides when given the lengths of other sides, as well as solving for missing side lengths when given the ratios of the sides.
By working through this worksheet, students will gain a better understanding of how proportions can be used to solve for missing lengths in triangles. They will also learn how to set up and solve proportions using cross-multiplication, which is a useful algebraic technique. Additionally, this worksheet will reinforce their knowledge of triangle properties and the relationship between the lengths of the sides.
Overall, the 7 5 proportions in triangles worksheet is a valuable tool for geometry students to practice and master the concept of proportions in triangles. It provides them with a variety of problems to solve, allowing them to strengthen their skills and gain confidence in their ability to use proportions to solve for missing side lengths in triangles.
What Are Proportions in Triangles?
In geometry, proportions in triangles refer to the relationships between the sides and angles of a triangle that can be expressed as ratios or fractions. These proportions can help us solve various problems and find missing measurements in triangles.
Ratios of Sides: One of the common proportions in triangles involves the ratios of the lengths of the sides. For example, the ratio of the lengths of two sides in a triangle can be equal to the ratio of the lengths of two other sides. This is known as the side- ratio proportion or the side-splitter theorem.
Ratios of Angles: Another type of proportion in triangles deals with the ratios of the measures of the angles. The ratio of the measures of two angles in a triangle can be equal to the ratio of the measures of two other angles. This is known as the angle-angle similarity or the AA similarity theorem.
Ratio of Sides to Perpendicular Segments: In some cases, we may also encounter proportions involving the sides of a triangle and the perpendicular segments from an angle to the opposite side. These proportions can be useful in solving problems related to right triangles.
Using Proportions to Solve Problems: Proportions in triangles can be used to find unknown side lengths, angle measures, or ratios of sides. By setting up an equation using the given proportions and solving for the unknown variable, we can determine the missing measurements in a triangle.
Overall, understanding proportions in triangles is essential in geometry as they provide a framework for solving various geometric problems and finding missing information in triangles.
Understanding Triangles and Their Sides
Triangles are one of the fundamental shapes in geometry, and they are studied extensively due to their simplicity yet complexity. Triangles consist of three sides and three angles, and understanding the relationship between these sides and angles is crucial in solving various geometric problems. One important concept in triangles is the idea of proportions.
Proportions play a significant role in triangles as they help determine the relationship between the sides. When it comes to proportions in triangles, one commonly encountered concept is the proportionality of side lengths. This means that if two triangles are similar, their corresponding sides are proportional.
For example, in a right triangle with sides measuring 3, 4, and 5 units, we can see that the proportion between the two shorter sides is 3:4, while the proportion between the hypotenuse and the shorter side is 5:3. This relationship holds true for any right triangle with side lengths in the same ratios. In other types of triangles, such as equilateral, isosceles, or scalene triangles, the proportions between the sides will vary depending on their specific properties.
Proportions in Triangles Worksheet
When studying proportions in triangles, it is common to come across worksheets that provide practice problems. These worksheets typically include a variety of triangle types and ask students to find the missing side lengths or determine whether two triangles are similar based on their sides. These worksheets help students develop their understanding of proportions in triangles and enhance their problem-solving skills.
One example of such a worksheet is the “7 5 proportions in triangles worksheet.” This worksheet might include questions like, “If two triangles have side lengths of 5 inches and 7 inches, and their corresponding sides are proportional, what is the length of the third side in the smaller triangle?” Students would then need to determine the missing side length using the given proportions.
In conclusion, understanding the proportions in triangles is vital in geometry as it allows us to determine the relationship between the sides of different triangles. Worksheets like the “7 5 proportions in triangles worksheet” help students practice these concepts and strengthen their problem-solving abilities.
The Basics of Triangles
Triangles are one of the most fundamental shapes in geometry. They are polygonal shapes with three sides and three angles. Understanding the different types of triangles and their properties is essential in many fields, including mathematics, engineering, and architecture.
There are several ways to classify triangles based on their sides and angles. In terms of sides, triangles can be categorized as equilateral, isosceles, or scalene. An equilateral triangle has three equal sides, while an isosceles triangle has two equal sides. A scalene triangle has three sides of different lengths. On the other hand, triangles can also be classified based on their angles. These classifications include acute, right, and obtuse triangles. An acute triangle has three angles less than 90 degrees, a right triangle has one 90-degree angle, and an obtuse triangle has one angle greater than 90 degrees.
Properties of Triangles
Triangles have several properties that are important to understand. The sum of the interior angles of a triangle is always 180 degrees. This property, known as the angle sum property, can be used to find the measure of a missing angle in a triangle. Additionally, the longest side of a triangle is always opposite the largest angle, according to the triangle inequality theorem.
To calculate the area of a triangle, one can use the formula: area = (base x height) / 2. The base and height of a triangle can be determined by drawing an altitude, which is a perpendicular line from one vertex to the opposite side. The length of the altitude is the height, and the length of the base is the segment of the opposite side that is intersected by the altitude.
- Types of triangles based on sides:
- Equilateral triangle: All sides are equal in length.
- Isosceles triangle: Two sides are equal in length.
- Scalene triangle: All sides have different lengths.
- Types of triangles based on angles:
- Acute triangle: All angles are less than 90 degrees.
- Right triangle: One angle is exactly 90 degrees.
- Obtuse triangle: One angle is greater than 90 degrees.
Conclusion
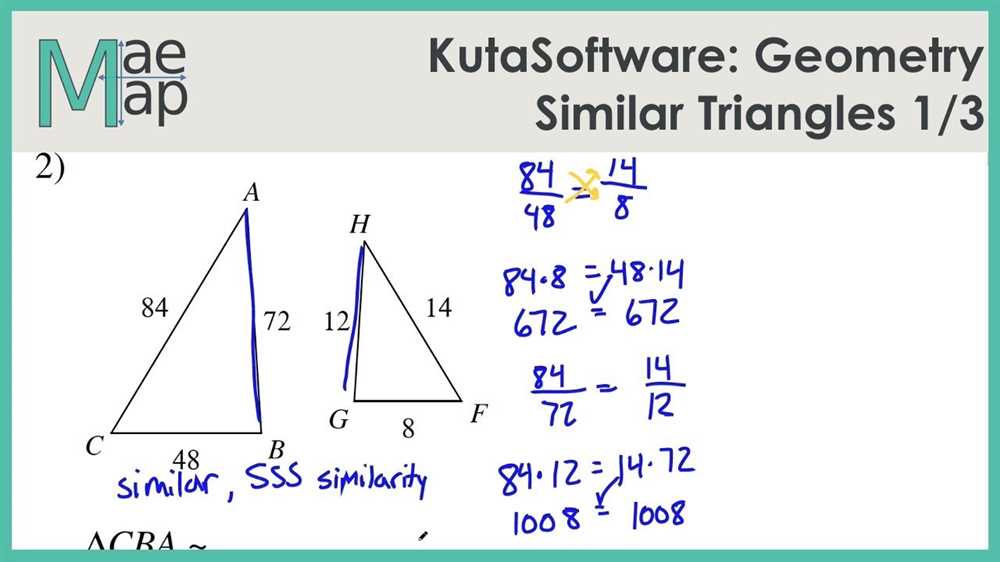
Triangles are fundamental geometric shapes with various classifications based on their sides and angles. Understanding the properties and formulas associated with triangles is crucial in many fields and can help solve problems and determine unknown values. By familiarizing oneself with the different types of triangles, their properties, and the formulas for calculating their area, one can gain a solid foundation in geometry.
A Closer Look at Triangle Sides
In the study of geometry, triangles play a fundamental role. One key aspect of triangles that we focus on is the relationship between their sides. By understanding the different types of triangles and their corresponding side lengths, we can unlock valuable insights into their properties and behavior.
Equilateral triangles are a special type of triangle where all three sides have the same length. This means that if one side is given a value, the other two sides will also have the same value. Equilateral triangles have the property that all three interior angles are also equal, measuring 60 degrees each. These triangles are often associated with symmetry and balance.
Isosceles triangles are another interesting type of triangle. In an isosceles triangle, two of the sides have the same length, while the third side is of a different length. This creates an unequal distribution of side lengths. The angles opposite the equal sides are also equal, creating a unique symmetry. Isosceles triangles are often used in architecture and design to create visually appealing structures.
Scalene triangles are the most general type of triangle. In a scalene triangle, all three sides have different lengths. This creates a dynamic and asymmetrical structure. The angles inside a scalene triangle are also different, adding to its unique character. Scalene triangles can be found in nature and are often used in engineering and construction to create complex shapes and structures.
In summary, the study of triangle sides allows us to understand the different relationships between their lengths and angles. Equilateral triangles have equal sides and angles, isosceles triangles have two equal sides and angles, and scalene triangles have different sides and angles. By recognizing these patterns, we can better analyze and interpret the properties and behavior of triangles in various contexts.
Proportional Relationships in Triangles
In geometry, proportional relationships play a crucial role in understanding the properties and measurements of triangles. These relationships involve the ratios between different parts of a triangle, such as its angles, side lengths, and area. By understanding and applying these proportional relationships, mathematicians can solve various problems related to triangles.
1. Side-Side-Side (SSS) Proportion: The SSS proportion states that if the lengths of the sides of two triangles are in proportion, then the triangles are similar. This means that their corresponding angles are congruent and their corresponding side lengths have the same ratio.
2. Angle-Angle (AA) Proportion: The AA proportion states that if two angles of one triangle are congruent to two angles of another triangle, then the triangles are similar. This means that their corresponding side lengths have a proportional relationship.
- For example, if ∠A = ∠D and ∠B = ∠E in two triangles, then the corresponding side lengths have a proportional relationship.
3. Side-Angle-Side (SAS) Proportion: The SAS proportion states that if the ratios of the lengths of two pairs of corresponding sides of two triangles are in proportion, and the included angles are congruent, then the triangles are similar. This means that their corresponding side lengths have a proportional relationship.
- For example, if the ratio of AB to DE is equal to the ratio of BC to EF, and ∠B = ∠E, then the triangles are similar.
4. Proportional Relationships in Right Triangles: In right triangles, proportional relationships can be used to solve for missing side lengths or to find trigonometric ratios. The most common proportional relationship is the trigonometric function sine, cosine, and tangent.
- The sine of an angle in a right triangle is equal to the ratio of the length of the side opposite the angle to the length of the hypotenuse.
- The cosine of an angle in a right triangle is equal to the ratio of the length of the side adjacent to the angle to the length of the hypotenuse.
- The tangent of an angle in a right triangle is equal to the ratio of the length of the side opposite the angle to the length of the side adjacent to the angle.
5. Proportional Relationships in Similar Triangles: When two triangles are similar, their corresponding angles are congruent, and their corresponding side lengths have a proportional relationship. This means that if the ratio of two corresponding side lengths in one triangle is equal to the ratio of the corresponding side lengths in another triangle, then the triangles are similar.
| Triangle 1 | Triangle 2 |
|---|---|
| Side AB | Side DE |
| Side BC | Side EF |
| Angle A | Angle D |
By understanding and applying these proportional relationships in triangles, mathematicians can analyze and solve problems involving triangles in various real-world scenarios, such as architecture, engineering, and physics.
Explaining Proportions in Triangles
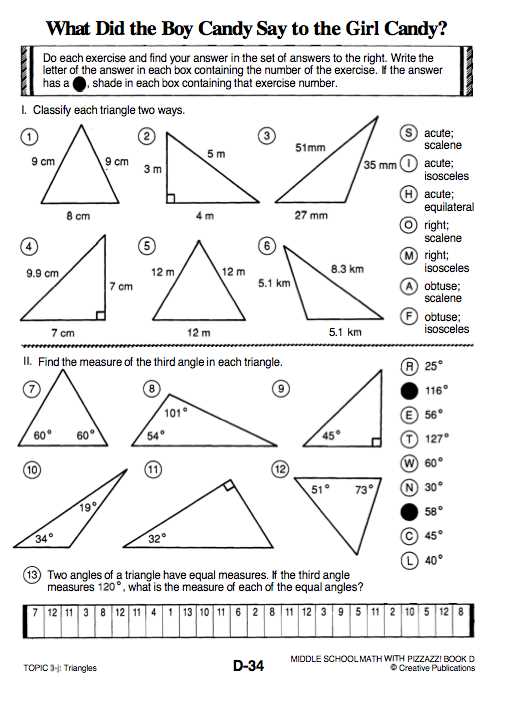
Proportions in triangles refer to the relationship between the different parts of a triangle, specifically the sides and angles. These proportions can help us understand and solve various problems in geometry. Let’s take a closer look at some of the key concepts and examples of proportions in triangles.
1. Similar Triangles: When two triangles have the same shape but different sizes, they are called similar triangles. The corresponding angles of similar triangles are equal, and the ratios of their corresponding sides are proportional. This property of similar triangles is the basis for many proportion calculations in triangle problems.
2. Side-Splitter Theorem: The side-splitter theorem states that if a line is parallel to one side of a triangle and intersects the other two sides, it divides those sides into proportional segments. This theorem allows us to find the lengths of segments within a triangle by using proportions.
- Example: In triangle ABC, line DE is parallel to side BC and intersects sides AB and AC. If AD = 4 cm, DB = 6 cm, and AE = 2 cm, what is the length of EC?
- Solution: Using the side-splitter theorem, we can set up the proportion: (AD/DB) = (AE/EC). Plugging in the given values, we get: (4/6) = (2/EC). Cross-multiplying, we find that EC = 3 cm.
3. Angle Bisector Theorem: The angle bisector theorem states that if a line segment bisects an angle of a triangle, it divides the opposite side into segments that are proportional to the other two sides. This theorem is often used to find missing side lengths in triangles.
- Example: In triangle ABC, angle bisector BD divides side AC into segments AD and DC. If AB = 8 cm, BC = 6 cm, and BD = 4 cm, what is the length of AD?
- Solution: Using the angle bisector theorem, we can set up the proportion: (AB/BC) = (AD/DC). Plugging in the given values, we get: (8/6) = (AD/(AC-AD)). Simplifying, we find: (8/6) = (AD/(14-AD)). Cross-multiplying and solving for AD, we find that AD = 5.6 cm.
By understanding and applying proportions in triangles, we can solve various geometry problems involving similarity, parallel lines, and angle bisectors. These concepts are fundamental to developing a strong understanding of geometric principles and problem-solving skills.