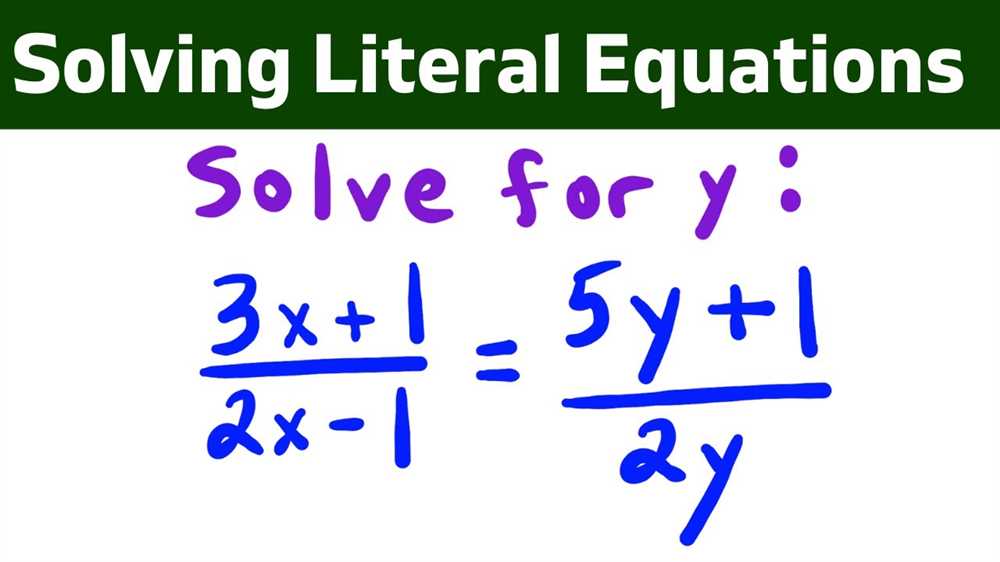
Literal equations are equations that involve multiple variables. They are often used to solve problems where the relationship between variables is not known. Understanding how to solve literal equations is an essential skill in algebra and can be applied to various real-life situations.
A literal equation coloring activity is a fun and engaging way for students to practice solving literal equations. These activities typically involve a set of equations with different variables and their corresponding answers. Students are required to solve the equations and color the answers based on a key or color code.
Providing answers to a literal equations coloring activity not only helps students check their work but also serves as a valuable learning tool. By comparing their answers to the correct ones, students can identify any mistakes they made and understand the correct approach to solving the equations. Additionally, providing answers allows students to self-assess their understanding and track their progress in solving literal equations.
Having access to literal equations coloring activity answers can be particularly helpful for teachers. It enables them to review the solutions and provide targeted feedback to students. Teachers can identify common mistakes or misconceptions and address them during class discussions or individualized instruction. The answers also serve as a valuable resource for teachers to plan and structure their lessons on solving literal equations.
What Is a Literal Equation?
A literal equation is an equation that contains one or more variables. Unlike regular equations, where you are solving for a specific value, a literal equation allows you to solve for a specific variable in terms of the other variables in the equation. Literal equations are commonly used in algebra and are a fundamental concept in mathematics.
In a literal equation, the variables are represented by letters, such as x, y, or z. These variables can represent any number or value. The goal is to isolate one variable on one side of the equation by performing various mathematical operations, such as addition, subtraction, multiplication, or division.
Litera equations are commonly used in various fields, including physics, engineering, and economics. They allow us to model and solve real-world problems by representing the relationship between different variables. By manipulating the equation, we can find relationships between variables and make predictions or solve for unknown values.
For example, in physics, the equation F = ma represents Newton’s second law of motion, where F is the force, m is the mass, and a is the acceleration. By rearranging the equation, we can solve for any one variable in terms of the other two. This allows us to calculate the force, mass, or acceleration given the values of the other variables.
Litera equations can be solved using algebraic methods or by using graphing calculators or computer software. They are an essential tool in problem-solving and critical thinking, as they require a deep understanding of mathematical relationships and how variables interact with each other.
Why Are Literal Equations Important?
Literal equations, also known as literal formulas, are mathematical equations that involve multiple variables. These equations play a crucial role in various fields, including physics, engineering, finance, and computer science. They help us model complex relationships between different quantities and solve problems that involve multiple unknowns.
One of the primary reasons why literal equations are important is that they allow us to express one variable in terms of others. This is particularly useful when we need to solve a problem where one variable depends on multiple others. By rearranging the equation and isolating the desired variable, we can easily compute its value based on the values of the other variables.
Literal equations are also essential for understanding and analyzing real-world situations. They provide a mathematical representation of relationships between various factors, allowing us to make predictions, optimize processes, and solve practical problems. For example, in physics, literal equations help us describe how different physical quantities, such as force, mass, and acceleration, are related.
Furthermore, literal equations are a fundamental tool in algebra and serve as the building blocks for more advanced mathematical concepts. They help develop problem-solving skills, logical reasoning, and mathematical thinking. By manipulating literal equations, students learn how to simplify expressions, solve for variables, and apply algebraic methods to solve complex problems.
In conclusion, literal equations are important because they enable us to represent complex relationships between variables, solve problems with multiple unknowns, analyze real-world situations, and develop algebraic problem-solving skills. They are an essential tool in various disciplines and help us better understand and manipulate mathematical
Exploring Literal Equations with a Coloring Activity

Literary equations are a fundamental concept in algebra and are often used to solve problems that involve multiple variables. To help students gain a better understanding of literal equations, a coloring activity can be a fun and engaging way to explore this topic. This activity allows students to practice solving literal equations while also incorporating a creative component.
The coloring activity begins with a set of literal equations that need to be solved for a specific variable. Students are provided with a worksheet that includes a variety of equations, each representing a different problem to be solved. The equations may involve algebraic expressions, fractions, or even exponents, depending on the level of the students.
Students start by solving each equation for the specified variable and identifying the correct solution. They can then use the solution to color in the corresponding section on a coloring sheet. This coloring sheet is designed to resemble a picture, with different sections representing different colors. As students solve each equation, they gradually fill in the picture with the designated colors, bringing it to life as they go.
This coloring activity not only reinforces the concept of literal equations but also allows students to practice their problem-solving skills. It encourages them to think critically and apply the mathematical concepts they have learned. Additionally, the creative aspect of coloring can help to keep students engaged and motivated throughout the activity.
In conclusion, using a coloring activity to explore literal equations can be an effective way to enhance students’ understanding of this topic. By combining problem-solving with a creative component, students can have an enjoyable and interactive learning experience. This activity allows them to see the practical application of literal equations while also honing their problem-solving skills.
Materials Needed for the Activity

In order to complete the literal equations coloring activity, you will need a few essential materials. These materials will help you understand and practice solving and manipulating literal equations while adding some fun and creativity to the process.
1. Coloring materials: You will need colored pencils, markers, or crayons to color the activity sheets. These coloring materials will allow you to differentiate between different parts of the equations and make the activity more visually appealing. Choose a variety of colors to add some vibrancy to your work.
2. Activity sheets: The activity sheets will contain literal equations that you need to solve and color. These sheets can be printed or provided to you in a digital format. Make sure you have access to the activity sheets before starting the activity.
3. Answer key: An answer key is crucial for self-checking your work and understanding the correct solutions. Make sure you have the answer key for the activity sheets you are working on. It will help you assess your progress and identify any mistakes you may have made.
4. Writing utensils: You will need a pencil or pen to solve the literal equations. Having a separate writing utensil will help keep your work neat and organized. It is recommended to use a pencil initially, as it allows for easier erasing in case you make any mistakes.
5. Workspace: Find a quiet and comfortable place where you can focus on the activity. Make sure you have enough space to spread out the activity sheets and have easy access to all the materials mentioned above.
Having these materials ready before starting the literal equations coloring activity will ensure a smooth and enjoyable experience. Take your time to understand the equations, solve them accurately, and let your creativity shine through with the coloring materials.
How to Use the Coloring Activity
The literal equations coloring activity is a fun and engaging way for students to practice solving literal equations while also incorporating a creative element. This activity can be used in a variety of educational settings, such as classrooms, homeschooling, or tutoring sessions. By following a few simple steps, students can effectively utilize this activity to enhance their understanding of literal equations.
Step 1: Familiarize yourself with the literal equations
Before starting the coloring activity, it is important to ensure that students have a solid understanding of literal equations and how to solve them. Provide a brief review or mini-lesson on the topic, highlighting any key concepts or strategies that will be used in the activity.
Step 2: Distribute the coloring activity sheets
Print out the coloring activity sheets, making sure each student has a copy. The sheets will typically include a variety of literal equations, each represented by a different color. Students will solve the equations and color the corresponding areas on the coloring sheet based on their solutions.
Step 3: Solve the literal equations
Working individually or in pairs, students should solve each literal equation on the sheet. They can use any appropriate method or strategy they have learned. Encourage them to show their work and explain their steps as they solve each equation.
Step 4: Color the areas based on the solutions

Once students have solved a literal equation, they should identify the correct color associated with the solution and color in the corresponding area on the coloring sheet. As they progress through the activity, students will create a visual representation of the solutions to the literal equations.
Step 5: Review and discuss the solutions

After completing the activity, take some time to review the solutions with the students. Discuss any common errors or misconceptions that may have arisen during the activity. This is also an opportunity to reinforce the concepts and strategies related to solving literal equations.
Overall, the literal equations coloring activity provides an interactive and engaging way for students to practice solving literal equations while also incorporating a creative element. By following the steps outlined above, students can reinforce their understanding of the topic and have fun in the process.
Finding Solutions to Literal Equations
Literal equations, also known as formula equations, involve variables and constants that need to be solved for a specific variable. These equations are used in various fields such as physics, engineering, and mathematics. Finding solutions to literal equations involves isolating the desired variable and manipulating the equation to solve for its value.
To find solutions to literal equations, it is important to first identify the variable that needs to be solved for. This variable is usually denoted by a letter, such as x, y, or z. Once the variable is identified, the equation is manipulated using algebraic steps to isolate the variable on one side of the equation.
For example, consider the equation to solve for the variable x in the formula for the area of a rectangle: A = l * w. To solve for x, the length and width of the rectangle are given values. By substituting these values into the equation, the equation becomes A = 5 * w. To isolate x, the equation can be rearranged to w = A / 5. The variable x has been successfully solved for and expressed in terms of the given values.
Literal equations can also involve multiple variables. In such cases, it is important to have enough information or additional equations to solve for the desired variable. It may be necessary to combine equations or use substitution to find the solution.
Overall, finding solutions to literal equations requires careful manipulation and understanding of mathematical principles. By identifying the desired variable and using algebraic steps, it is possible to solve for the unknown variable and find its value.
Solving Literal Equations Step-by-Step
When it comes to solving literal equations, it’s important to follow a step-by-step approach in order to find the solution. Literal equations involve variables and constants, and the goal is to isolate a specific variable in the equation.
The first step in solving a literal equation is to identify the variable that needs to be isolated. Look at the equation and determine which variable you want to solve for. Once you have identified the variable, you can move on to the next step.
The second step is to use inverse operations to isolate the variable. This involves performing the same operation to both sides of the equation in order to cancel out any terms. For example, if you have an equation with addition, you can subtract the same value from both sides. If you have an equation with multiplication, you can divide both sides by the same value.
After isolating the variable, you may need to simplify the equation further. This can involve combining like terms or using the distributive property to eliminate any parentheses. Simplification helps to make the equation more manageable and easier to solve.
Finally, check your solution by substituting the value you found back into the original equation. If the equation is true with the substituted value, then your solution is correct. If not, go back and double-check your work to find any errors.
Following these steps will help you successfully solve literal equations and find the desired variable. Practice and understanding of the properties and operations involved in solving equations will improve your skills in this area.