
If you’re studying quadratic equations and factoring, you may have come across the term “Csi factoring and quadratics.” This method combines the principles of factoring and quadratic equations to help you solve complex problems. In this article, we’ll provide you with an answer key to help you understand and solve Csi factoring and quadratics problems.
Quadratic equations involve terms of the form ax^2 + bx + c = 0, where a, b, and c are constants. Factoring is a method used to break down a quadratic equation into its constituent parts. Csi factoring and quadratics takes this a step further by incorporating clues and hints to solve the equation, much like a crime scene investigation.
In order to successfully solve Csi factoring and quadratics problems, it’s important to identify the factors of the constant term (c) and the factors that add up to the coefficient of the linear term (b). By using these clues, you can determine the values of x that satisfy the equation. Our answer key will provide step-by-step solutions to guide you through the process and ensure you arrive at the correct answer.
Csi Factoring and Quadratics Answer Key
The “Csi Factoring and Quadratics” activity is a fun and engaging way for students to practice their factoring skills while solving a crime. In this activity, students are presented with a crime scene and a set of clues. They must use their knowledge of factoring and quadratics to solve the crime by determining the correct answer key.
The answer key for the “Csi Factoring and Quadratics” activity includes the solutions to the factoring problems presented in the activity. It provides the correct factors of the quadratic expressions and helps students verify their answers. The answer key also includes any necessary steps or explanations to arrive at the correct solution.
Example Answer Key:
- Problem 1: Factor the quadratic expression: x^2 + 5x + 6
- Answer: (x + 2)(x + 3)
- Problem 2: Factor the quadratic expression: 2x^2 – 7x – 15
- Answer: (2x + 3)(x – 5)
- Problem 3: Factor the quadratic expression: 4x^2 + 12x + 9
- Answer: (2x + 3)^2
The “Csi Factoring and Quadratics Answer Key” provides a helpful resource for both students and teachers. It allows students to check their work and understand any mistakes or areas for improvement. Teachers can also use the answer key as a guide to assess student understanding and provide feedback.
Overall, the “Csi Factoring and Quadratics Answer Key” is an essential tool in the “Csi Factoring and Quadratics” activity, assisting students in solving the crime by correctly factoring the quadratic expressions.
Overview
Welcome to CSI Factoring and Quadratics! In this interactive activity, you will be tasked with solving a series of quadratic equations and factoring various polynomial expressions. These skills are essential in algebra and have real-life applications in fields such as engineering, physics, and computer science.
The activity is divided into several parts, starting with a brief introduction to quadratics and factoring. You will then proceed to solve quadratic equations by factoring, completing the square, and using the quadratic formula. Each method will be explained in detail, and you will have multiple examples to practice with.
Once you have mastered solving quadratic equations, you will move on to factoring polynomials. This involves finding the factors of a polynomial expression, which can provide valuable information about its graph and roots. You will learn various factoring techniques, such as factoring by grouping, factoring trinomials, and using special product patterns.
The goal of this activity is to improve your ability to solve quadratic equations and factor polynomials, as well as enhance your critical thinking and problem-solving skills. Remember to take your time, ask questions when needed, and practice regularly. Good luck!
What is CSI Factoring?
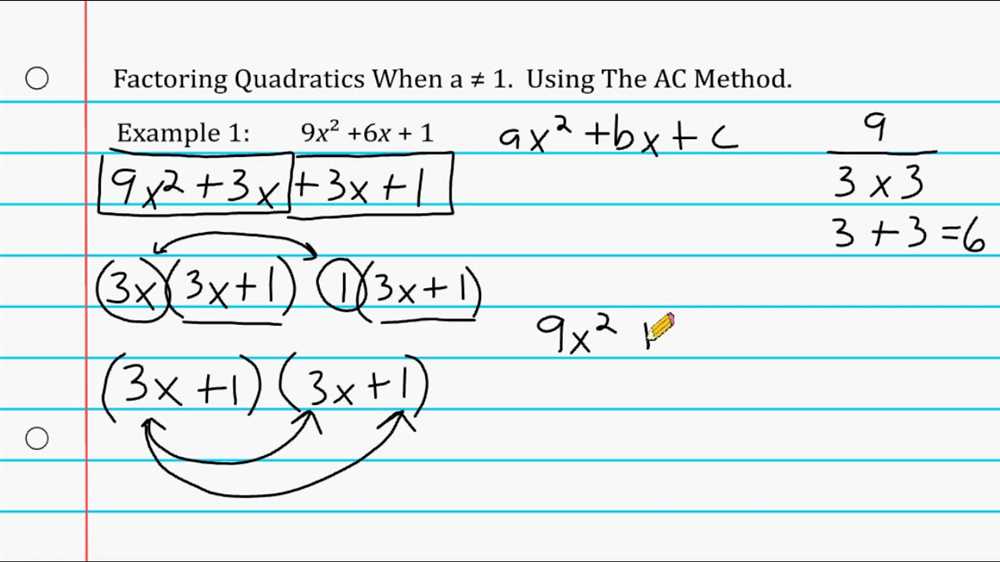
CSI Factoring is a method used in algebra to factor quadratic expressions. It stands for the coefficient, sign, and integer method, which are the three key components involved in the factoring process. This method is especially useful in solving quadratic equations and simplifying expressions.
The coefficient refers to the numerical value in front of the variable, which is usually represented by the letter “a” in the quadratic expression. The sign refers to whether the quadratic term is positive or negative. And the integer represents the constant term at the end of the expression. These three components play a crucial role in determining how the quadratic expression can be factored.
To use the CSI method, you first identify the values of “a,” the sign, and the integer. Then you use these values to find the factors of the quadratic expression by finding two numbers that multiply to give the product of “a” and the integer, and add up to give the coefficient.
Example:
Let’s say we have the quadratic expression: 3x^2 + 7x + 2. Using the CSI method, we can determine that “a” is 3, the sign is positive, and the integer is 2. The factors of 3 and 2 are 1, 3, -1, and -3. We need to find two numbers from these factors that add up to 7, which is the coefficient. In this case, the numbers are 1 and 2. Therefore, we can express the quadratic equation as (x + 1)(3x + 2).
CSI Factoring provides a systematic approach to factor quadratic expressions and solve quadratic equations. It is a useful tool in algebra and can be applied to various mathematical problems. Understanding this method allows students to simplify expressions and solve equations more efficiently.
CSI Factoring is a method used in mathematics to solve quadratic equations. It involves breaking down a quadratic equation into its factors to find the value(s) of the unknown variable. This method is particularly useful in simplifying complex equations and solving for roots or solutions.
The process of CSI Factoring involves identifying the quadratic equation in the form of ax^2 + bx + c = 0, where a, b, and c are coefficients. The first step is to factor out the greatest common factor (GCF) from all the terms of the equation. This simplifies the equation and makes it easier to factorize.
Once the GCF is factored out, the equation is grouped into pairs of terms. The goal is to find two terms that add up to the coefficient of the middle term, bx. These terms should also multiply to give the constant term, c. By grouping the terms and rearranging them, it becomes possible to factorize the equation further.
The next step in the CSI Factoring process is to factorize the equation using various methods such as the difference of squares, perfect square trinomials, or quadratic trinomials. By factoring the equation, it becomes possible to find the values of x that satisfy the equation. These values are called the roots or solutions of the quadratic equation.
In conclusion, CSI Factoring is a useful tool in solving quadratic equations. By breaking down the equation into its factors, it becomes easier to find the values of the unknown variable and solve for the roots. This method simplifies complex equations and allows for a more efficient and systematic approach to problem-solving in mathematics.
Why is Factoring Important in Quadratics?

Factoring plays a crucial role in working with quadratic equations as it allows us to simplify and solve these complex mathematical expressions. By factoring a quadratic equation, we can break it down into more manageable components, making it easier to analyze and understand the behavior of the equation.
One of the main reasons factoring is important in quadratics is that it helps us find the solutions or roots of the equation. By factoring a quadratic equation into its linear factors, we can set each factor equal to zero and solve for the value of the variable. This process is known as finding the zeros or x-intercepts of the equation, and it provides us with valuable information about the graph and behavior of the quadratic equation.
Furthermore, factoring quadratics allows us to identify key attributes of the equation, such as the vertex, axis of symmetry, and maximum or minimum points. By factoring the quadratic equation into its standard form, we can easily determine these important characteristics and use them to analyze and graph the equation.
In addition to solving the equation and identifying key attributes, factoring is also crucial in simplifying and manipulating quadratic expressions. It allows us to reduce complex quadratic expressions into simpler forms, which can be helpful in various mathematical calculations and applications.
In conclusion, factoring is a fundamental concept in working with quadratics as it enables us to simplify and solve these equations, find the solutions, identify key attributes, and manipulate the expressions. Therefore, understanding and utilizing factoring techniques is essential for mastering quadratic equations and their applications in various fields such as mathematics, physics, and engineering.
Understanding the Quadratic Formula

The quadratic formula is a fundamental tool in solving quadratic equations. It allows us to find the values of the variable x that satisfy the equation ax^2 + bx + c = 0, where a, b, and c are constants. The equation can have two, one, or no real solutions, depending on the discriminant value obtained from the formula.
The quadratic formula is:
x = (-b ± √(b^2 – 4ac)) / 2a
The formula is derived from completing the square technique and can be used for any quadratic equation, regardless of the values of a, b, and c. The numerator of the formula represents the additive and subtractive components, which account for the two possible solutions, while the denominator ensures the correct scaling of the solutions.
To use the quadratic formula, you need to identify the values of a, b, and c from the given quadratic equation. Then, substitute these values into the formula and simplify the expression by performing the necessary calculations. The resulting solutions will provide the values of x that satisfy the equation.
It is important to note that the discriminant (b^2 – 4ac) obtained from the formula can help determine the nature of the solutions. If the discriminant is positive, the equation has two distinct real solutions. If the discriminant is zero, the equation has one real solution. And if the discriminant is negative, the equation has no real solutions, but it will have complex solutions involving imaginary numbers.
Using the CSI Factoring Answer Key
When it comes to solving quadratic equations, the CSI Factoring Answer Key is an invaluable tool. This answer key provides step-by-step solutions to factoring quadratics, making it easier for students to understand and practice this important concept in algebra.
By using the CSI Factoring Answer Key, students can learn the process of factoring quadratics and apply it to solve a wide range of quadratic equations. The answer key breaks down each step of the factoring process, from identifying the factors to simplifying the equation. This allows students to see the logic behind the process and develop a deeper understanding of how to factor quadratics.
One of the key advantages of using the CSI Factoring Answer Key is that it provides confidence to students as they navigate through challenging quadratic equations. It serves as a reference guide that students can rely on when they encounter difficult problems. By following the steps outlined in the answer key, students can feel reassured that they are on the right track and can successfully factor the given quadratic equation.
In addition, the CSI Factoring Answer Key offers a valuable opportunity for self-assessment. Students can compare their own solutions to the answer key and identify any mistakes or misunderstandings they may have. This allows them to improve their problem-solving skills and gain a better understanding of the concept of factoring quadratics.
To sum up, the CSI Factoring Answer Key is a powerful tool in learning and mastering the process of factoring quadratics. By using this answer key, students can gain confidence, improve their problem-solving skills, and develop a deep understanding of this important algebraic concept.
Exercises to Practice Factoring and Quadratics

Factoring and solving quadratic equations are important skills in mathematics. These exercises will help you practice these skills and improve your understanding of factoring and quadratics.
1. Factor the following quadratic expressions:
- x2 + 5x + 6: This quadratic expression can be factored as (x + 2)(x + 3).
- 2x2 – 9x + 4: This quadratic expression can be factored as (2x – 1)(x – 4).
- 3x2 + 10x + 8: This quadratic expression can be factored as (3x + 2)(x + 4).
2. Solve the following quadratic equations:
- x2 – 4x – 5 = 0: To solve this equation, factor the quadratic expression as (x – 5)(x + 1) = 0. Therefore, x = 5 or x = -1.
- 2x2 + 7x – 15 = 0: To solve this equation, factor the quadratic expression as (2x – 3)(x + 5) = 0. Therefore, x = 3/2 or x = -5.
- 4x2 – 9x + 2 = 0: To solve this equation, factor the quadratic expression as (4x – 1)(x – 2) = 0. Therefore, x = 1/4 or x = 2.
3. Use factoring to simplify the following quadratic expressions:
- 3x2 – 9x + 6: This quadratic expression can be simplified by factoring out a common factor of 3, resulting in 3(x2 – 3x + 2).
- 6x2 + 12x + 6: This quadratic expression can be simplified by factoring out a common factor of 6, resulting in 6(x2 + 2x + 1).
- 5x2 – 20x + 15: This quadratic expression can be simplified by factoring out a common factor of 5, resulting in 5(x2 – 4x + 3).
These exercises will help you develop your factoring and quadratic solving skills. Practice regularly to improve your proficiency in these important mathematical concepts.