In the field of statistics, histograms and dot plots are two common graphical representations used to display data. They provide a visual way to understand the distribution of a dataset and identify any patterns or trends that may be present. In this article, we will be discussing the answer key for a worksheet on histograms and dot plots, which will help students practice their skills in interpreting and creating these types of graphs.
The answer key for the worksheet on histograms and dot plots includes a set of data points, along with the corresponding histogram and dot plot. Students can use this answer key to check their work and verify whether they have correctly constructed the graphs and interpreted the data. It also provides a reference for understanding how the data is represented and organized in each graph.
By using the answer key, students can gain a better understanding of how to interpret histograms and dot plots. They can compare their own graphs to the answer key and identify any discrepancies or errors in their work. This allows them to learn from their mistakes and improve their skills in creating accurate and informative graphs.
Histograms and Dot Plots Worksheet Answer Key
In the study of statistics, histograms and dot plots are two graphical representations used to display the distribution of a dataset. A histogram is a bar chart that shows the frequencies or relative frequencies of different intervals or classes in a dataset. On the other hand, a dot plot is a simple diagram that uses dots to represent the occurrence of a value in a dataset.
When analyzing a histogram or dot plot, the key components to look for include the shape, center, and spread of the data. The shape of the histogram or dot plot can be categorized as symmetric, skewed left, or skewed right. The center of the data can be identified by locating the peak or mode in a histogram, or by finding the median in a dot plot. The spread of the data can be observed by examining the range, interquartile range, or standard deviation.
In the Histograms and Dot Plots Worksheet Answer Key, students will find the correct answers and explanations for the given problems. This answer key will help them verify their understanding of histograms and dot plots, and provide guidance on how to interpret and analyze the data. It will also serve as a useful resource for teachers, allowing them to assess their students’ comprehension and progress in the topic of histograms and dot plots.
In conclusion, the Histograms and Dot Plots Worksheet Answer Key is a valuable tool for students and teachers in the field of statistics. It provides the necessary information to properly interpret and analyze histograms and dot plots, and allows for self-assessment and progress tracking. Understanding these graphical representations is essential in the study of statistics, as they help in making data-driven decisions and drawing valid conclusions.
Understanding Histograms
Histograms are visual representations of data that provide valuable insights into the distribution and frequency of a dataset. They are particularly useful when dealing with large datasets or when trying to identify patterns or anomalies in the data. In a histogram, data is grouped into bins, and the height of each bin represents the frequency or count of data points falling within that range. This allows us to easily identify the most common or prevalent values in the dataset.
When interpreting a histogram, it is important to pay attention to the shape, center, and spread of the distribution. The shape of the histogram can tell us whether the data is symmetric, skewed to the right or left, bimodal, or has multiple peaks. The center of the distribution can be determined by finding the bin with the highest frequency, while the spread of the distribution can be assessed by looking at the range of values that fall within a certain number of standard deviations from the mean.
Here are a few key points to keep in mind when understanding histograms:
- A histogram can provide insights into the underlying patterns and distribution of a dataset.
- The shape, center, and spread of a histogram can help us analyze and interpret the data more effectively.
- The height of each bin in a histogram represents the frequency or count of data points falling within that range.
- By analyzing the histogram, we can identify outliers, clusters, or gaps in the data.
- Histograms are particularly useful when dealing with large datasets, as they provide a visual summary of the data.
Overall, histograms are powerful tools for data analysis and visualization. They allow us to understand the distribution of data and identify patterns or anomalies that may not be immediately apparent from the raw numbers. By interpreting histograms correctly, we can make informed decisions and draw meaningful conclusions from the data.
Key Components of a Histogram
A histogram is a graphical representation of the distribution of a dataset. It displays the frequency of values in different intervals, or bins, along a horizontal axis. Understanding the key components of a histogram is crucial for interpreting and analyzing data.
1. Horizontal Axis (x-axis): The horizontal axis of a histogram represents the range of values in the dataset. It is divided into equal intervals or bins, which determine the width and location of each bar in the histogram. The range of values covered by the horizontal axis should encompass the entire dataset.
2. Vertical Axis (y-axis): The vertical axis of a histogram represents the frequency or count of values falling within each bin. It shows the number of observations or occurrences of values in the dataset. The scale of the vertical axis should be appropriately chosen to clearly display the frequency distribution.
3. Bins: Bins are intervals or ranges into which the data is divided. Each bin in a histogram represents a group of values falling within that range. The width and number of bins determine the level of detail in the histogram. Too few bins can oversimplify the distribution, while too many bins can make it difficult to interpret the data.
4. Bars: The bars in a histogram are vertical rectangles that represent the frequency or count of values falling within each bin. The height of the bars corresponds to the frequency of values in that bin. The width of each bar is determined by the width of the corresponding bin on the horizontal axis.
5. Title: The title of a histogram provides a brief description of the dataset or the variable being represented. It gives the reader an idea of what the histogram is showing and helps in conveying the main message or finding of the data analysis.
6. Axes Labels: The axes labels provide information about the values being represented on the horizontal and vertical axes. They should be clear and concise, indicating the variable and units of measurement, if applicable.
Understanding these key components of a histogram is essential for accurately interpreting and analyzing data. By examining the distribution of values and the frequency of occurrences, histograms provide valuable insights into the shape, central tendency, and variability of a dataset.
Analyzing Histograms
Histograms are graphical representations of data that display the frequency distribution of a set of continuous or discrete variables. They are particularly useful for analyzing the shape, center, and spread of a dataset. By examining the histogram, we can gain insights into the underlying patterns and characteristics of the data.
One key aspect of analyzing histograms is understanding the shape of the distribution. The shape can provide information about the symmetry or skewness of the data. For example, a symmetric histogram indicates that the data is evenly distributed around the center, while a skewed histogram suggests that the data is concentrated more on one side.
In addition to shape, histograms also provide information about the center and spread of the data. The center is represented by the peak or mode of the histogram, which indicates the most common value in the dataset. The spread, on the other hand, can be determined by the range or width of the bars in the histogram.
Furthermore, histograms allow for the identification of outliers or unusual values in the dataset. Outliers are data points that significantly deviate from the overall pattern of the data. By visually examining the histogram, we can easily spot these outliers and assess their impact on the overall distribution.
In conclusion, histograms are powerful tools for analyzing and interpreting data. They provide valuable insights into the shape, center, spread, and outliers of a dataset, allowing us to make informed decisions and draw meaningful conclusions.
Creating a Histogram from Data
In statistics, a histogram is a graphical representation of data that uses rectangular bars to represent the frequency or proportion of different categories or intervals of a variable. It is a type of bar graph that provides a visual representation of the distribution of data.
To create a histogram from data, you first need to decide on the intervals or bins that will be used to group the data. These intervals should be chosen based on the range and distribution of the data, so that each interval represents a meaningful and distinct category. The number of intervals can vary depending on the amount of data and the level of detail desired.
Once the intervals are determined, you can begin creating the histogram. Start by labeling the x-axis with the intervals or categories, and the y-axis with the frequency or proportion of data points within each interval. Then, for each data point, determine which interval it falls into and count the number of data points in each interval.
After counting the data points in each interval, you can represent the frequency or proportion using rectangular bars on the graph. The height of each bar corresponds to the frequency or proportion, and the width of the bar should be consistent across all intervals. The bars should be positioned directly above the corresponding interval on the x-axis.
Once the histogram is complete, you can analyze the distribution of the data. The shape of the histogram can provide insights into the central tendency, variability, and skewness of the data. It can also help identify any outliers or unusual patterns in the data. Histograms are particularly useful for displaying continuous numerical data and can be a valuable tool in data analysis and decision-making.
Interpreting Dot Plots
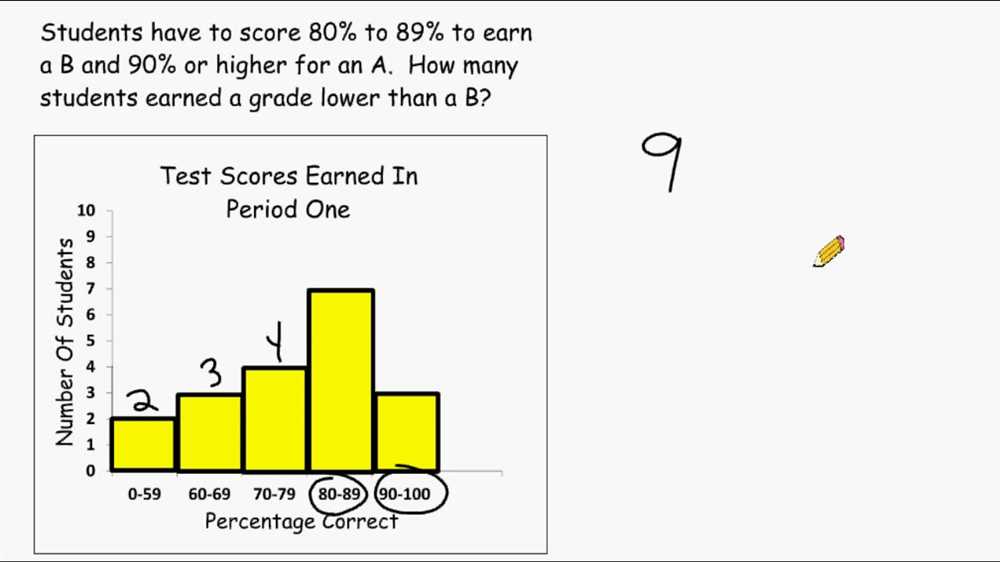
A dot plot is a visual representation of data where each data point is represented by a dot on a number line. It is a useful tool for analyzing the distribution and spread of data. By interpreting a dot plot, we can gain insights into the frequency and variability of the data set.
To interpret a dot plot, we first look at the number line and identify the range of values. The number line is divided into equal intervals, and each dot represents a data point. The vertical column of dots at each value represents the frequency or count of that value. By observing the distribution of dots, we can identify patterns, outliers, and central tendencies in the data.
For example, if we have a dot plot of the heights of students in a class, we can easily see the range of heights and which heights are most common. If the dots are clustered around a certain value, it indicates a central tendency. If there are outliers, they will appear as individual dots outside the main cluster.
By analyzing the dot plot, we can answer questions like: What is the most common height in the class? Are there any unusual height values? How is the data spread out? Is there a pattern or trend in the data?
In conclusion, dot plots provide a visual representation of data that helps us interpret the distribution, frequency, and variability of a data set. By analyzing the dot plot, we can gain valuable insights into the data and make informed decisions based on the patterns and trends observed.
Constructing a Dot Plot
A dot plot is a graphical representation of data that uses dots to represent individual data points. It is a simple and effective way to display the distribution of a dataset. To construct a dot plot, follow these steps:
- Start by drawing a number line that spans the range of the dataset, from the minimum value to the maximum value. Label the number line with appropriate increments.
- List each value from the dataset above the number line.
- For each value, place a dot directly above the corresponding number on the number line.
- If there are repeated values in the dataset, stack the dots vertically above the corresponding number on the number line.
- Provide a clear title for the dot plot and label the axes if necessary.
- Interpret the dot plot by examining the distribution of the dots. Look for patterns, clusters, or outliers that may provide insights into the data.
Dot plots are particularly useful when the dataset is small or when the distribution of the data is not easily captured by other types of graphs. They allow individuals to quickly visualize the spread and concentration of the data, making it easier to identify trends or anomalies.
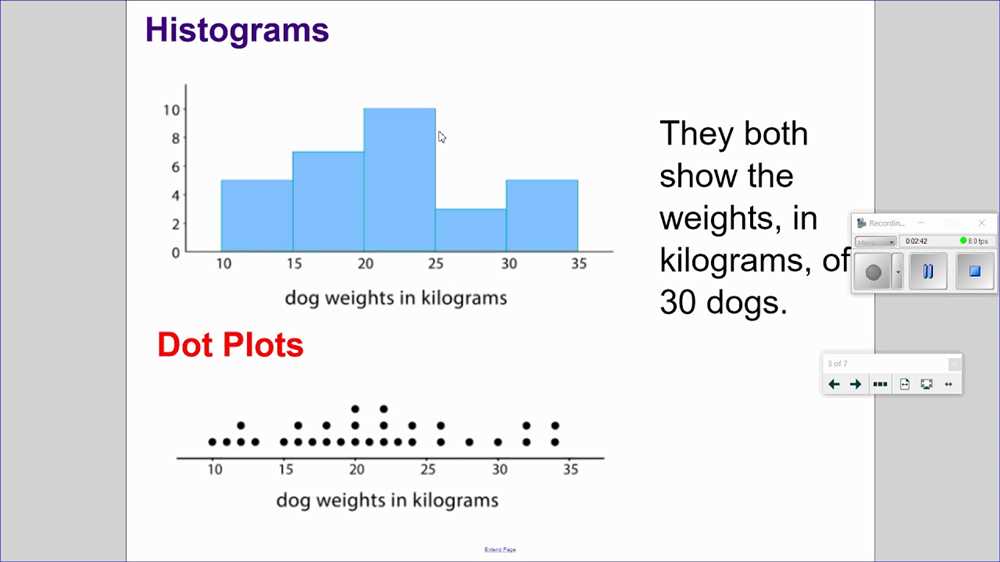
Comparing Histograms and Dot Plots
When analyzing data, we often use different visual representations to help us understand the distribution and patterns within the data. Two common types of graphical representations are histograms and dot plots.
A histogram is a bar graph that represents the frequency of data within different intervals, or bins. The height of each bar corresponds to the frequency or count of data points within that bin. Histograms are useful for displaying continuous data and identifying the shape of the distribution, such as whether it is symmetric, skewed, or bimodal.
On the other hand, a dot plot displays each data point individually along a number line. Each dot represents one data point, and they are stacked vertically when there are multiple data points with the same value. Dot plots are particularly effective for showing the exact values of data points and identifying any outliers or gaps within the data.
Comparing histograms and dot plots can provide insight into the distribution and characteristics of the data. By examining the shape of the histogram, we can observe the central tendency and variability of the data. Dot plots allow for a more precise examination of individual data points and can reveal any patterns or clusters.
It is important to note that both histograms and dot plots have their own advantages and limitations. They are most effective when used in conjunction with each other to gain a comprehensive understanding of the data. By comparing and contrasting the information provided by these graphical representations, we can make more informed conclusions and insights about the data and its underlying patterns.