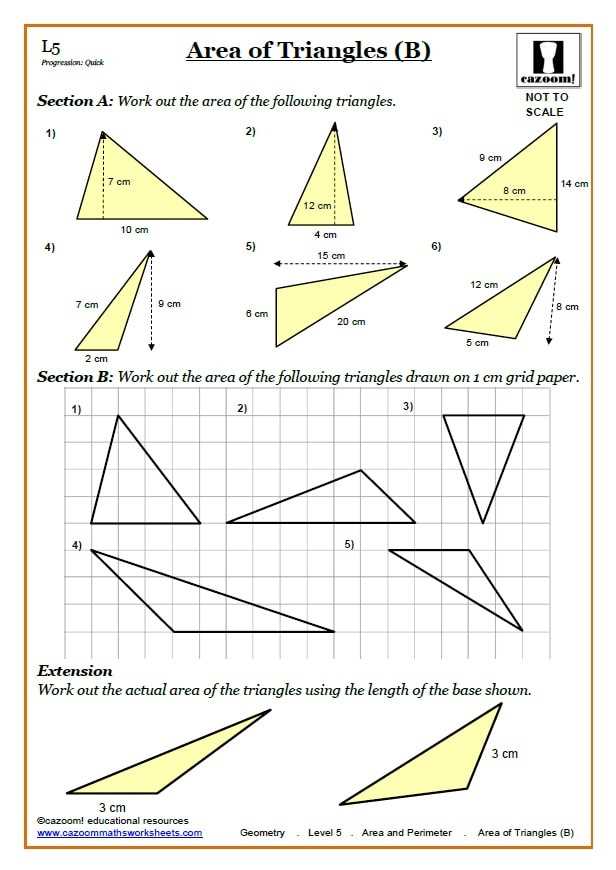
Calculating the area of mixed shapes can be a challenging task. These shapes often require breaking them down into simpler, recognizable shapes to find their individual areas and then adding them together. Having an answer key can greatly help in determining the correct areas and ensuring accurate calculations.
An area mixed shapes answer key provides a comprehensive list of formulas and step-by-step solutions for various mixed shapes. It includes different types of shapes, such as rectangles, triangles, circles, and more, that may be combined to form a complex shape. By referring to the answer key, students and learners can find the correct formulas and methods to calculate the areas of these mixed shapes.
Using an answer key not only helps in finding the correct areas but also aids in understanding the process of solving mixed shape problems. It provides explanations and examples to guide learners through the steps involved in determining the area. This can be especially useful for individuals studying mathematics or geometry, as it provides a visual representation of problem-solving techniques.
Furthermore, an area mixed shapes answer key allows for self-assessment and practice. Students can compare their own calculations to the solutions provided in the answer key to check for accuracy. It serves as a helpful tool for identifying any mistakes or misunderstandings and provides an opportunity for further learning and improvement.
Area Mixed Shapes Answer Key
Calculating the area of mixed shapes can sometimes be challenging, but with the help of the answer key, it becomes much easier. By using the provided key, you can quickly find the area of various shapes that have been combined into one larger shape. This answer key serves as a guide, assisting you in determining the correct measurements and formulas to use when calculating the area. With the answer key, you can save time and ensure accuracy in your calculations.
The area mixed shapes answer key typically includes the measurements of each individual shape within the larger shape, along with the corresponding formulas needed to find their areas. It may also provide step-by-step instructions on how to calculate the area of the combined shape. By following the instructions and using the correct formulas, you can confidently find the area without the need for guesswork or trial and error.
Additionally, the answer key may include examples or sample problems, allowing you to practice calculating the area of mixed shapes before attempting the actual problem. This helps build your understanding and proficiency in working with these types of shapes. The answer key serves as a valuable tool for both students and teachers, providing clear explanations and solutions to complex area calculations.
In conclusion, the area mixed shapes answer key is a valuable resource for calculating the area of combined shapes. It provides the necessary measurements, formulas, and instructions to accurately determine the area. By utilizing the answer key, you can confidently solve problems involving mixed shapes and enhance your understanding of the concepts involved.
Understanding Area
The concept of area is fundamental in geometry and plays a crucial role in many scientific and practical applications. Area refers to the amount of space occupied by a two-dimensional object or shape. It is measured in square units, such as square meters, square inches, or square feet. Understanding the concept of area allows us to quantify and compare the size or extent of different shapes and objects.
To calculate the area of a simple shape, such as a square or rectangle, we can use the formula: area = length x width. For example, if we have a rectangle with a length of 5 meters and a width of 3 meters, the area would be 5 x 3 = 15 square meters. This formula can also be applied to parallelograms, where length represents the base and width represents the height.
When dealing with more complex shapes, such as triangles or circles, we need to use specific formulas tailored to these shapes. For example, the area of a triangle can be calculated using the formula: area = 1/2 x base x height. The base represents the length of the triangle’s bottom side, and the height represents the perpendicular distance from the base to the opposite vertex. For circles, the area can be calculated using the formula: area = π x radius^2, where π is a mathematical constant approximately equal to 3.14159.
It is important to note that the area of irregular or mixed shapes can be determined by breaking them down into simpler shapes. By dividing a mixed shape into smaller shapes, calculating their individual areas, and then summing them up, we can find the total area of the irregular shape.
Understanding and being able to calculate the area of shapes is essential for various fields, including architecture, engineering, interior design, and landscaping. It helps professionals estimate materials needed for construction projects, determine land space for building structures, and optimize space usage in interior design. Additionally, understanding area is also useful in everyday life, such as calculating the area of a room for flooring or estimating the amount of paint needed for a wall.
Overall, area is a fundamental concept in geometry that allows us to measure and compare the size of different shapes. By employing specific formulas for various shapes, we can calculate their areas and use this knowledge in both academic and practical settings.
Basic Formulas for Area Calculation
In geometry, the area of a shape refers to the measure of the space enclosed by its boundary. Calculating the area of different shapes is an essential skill in mathematics and is used in various real-life scenarios, such as construction and design. To determine the area of a shape, specific formulas are applied based on the shape’s characteristics and dimensions. Here are some basic formulas for area calculation.
1. Rectangle:
For a rectangle, the area can be calculated by multiplying the length by the width. The formula for the area of a rectangle is:
Area = Length x Width
2. Triangle:
The area of a triangle can be found by multiplying the base by the height and dividing the result by 2. The formula for the area of a triangle is:
Area = (Base x Height) / 2
3. Circle:
To calculate the area of a circle, the formula involves using the radius. The area can be found by multiplying the square of the radius by π (pi). The formula for the area of a circle is:
Area = π x (Radius^2)
It is important to remember that these are just some basic formulas for area calculation. Depending on the complexity of the shape, additional formulas or techniques may be required. By understanding and applying these basic formulas, you can easily find the area of various shapes and solve problems involving measurements and dimensions.
Calculating Area of Regular Shapes
Calculating the area of regular shapes is an important skill in geometry. Regular shapes are those that have all sides equal in length and all angles equal. Some common examples of regular shapes include squares, rectangles, triangles, and circles.
To calculate the area of a square, you simply need to know the length of one side. The formula for the area of a square is A = s^2, where A represents the area and s represents the length of one side. For example, if a square has a side length of 5 units, the area would be 5^2 = 25 square units.
For rectangles, the formula for calculating area is A = l x w, where A represents the area, l represents the length, and w represents the width. Let’s say we have a rectangle with a length of 6 units and a width of 4 units. The area would be 6 x 4 = 24 square units.
Triangles have their own formula for calculating area, which is A = 1/2 x b x h, where A represents the area, b represents the base, and h represents the height. For example, if a triangle has a base length of 8 units and a height of 6 units, the area would be 1/2 x 8 x 6 = 24 square units.
Lastly, circles have their own unique formula for calculating area, which is A = πr^2, where A represents the area and r represents the radius. The value of π is approximately 3.14. If a circle has a radius of 5 units, the area would be 3.14 x 5^2 = 78.5 square units.
By understanding and applying these formulas, you can confidently calculate the area of regular shapes in geometry.
Area of Triangles and Quadrilaterals
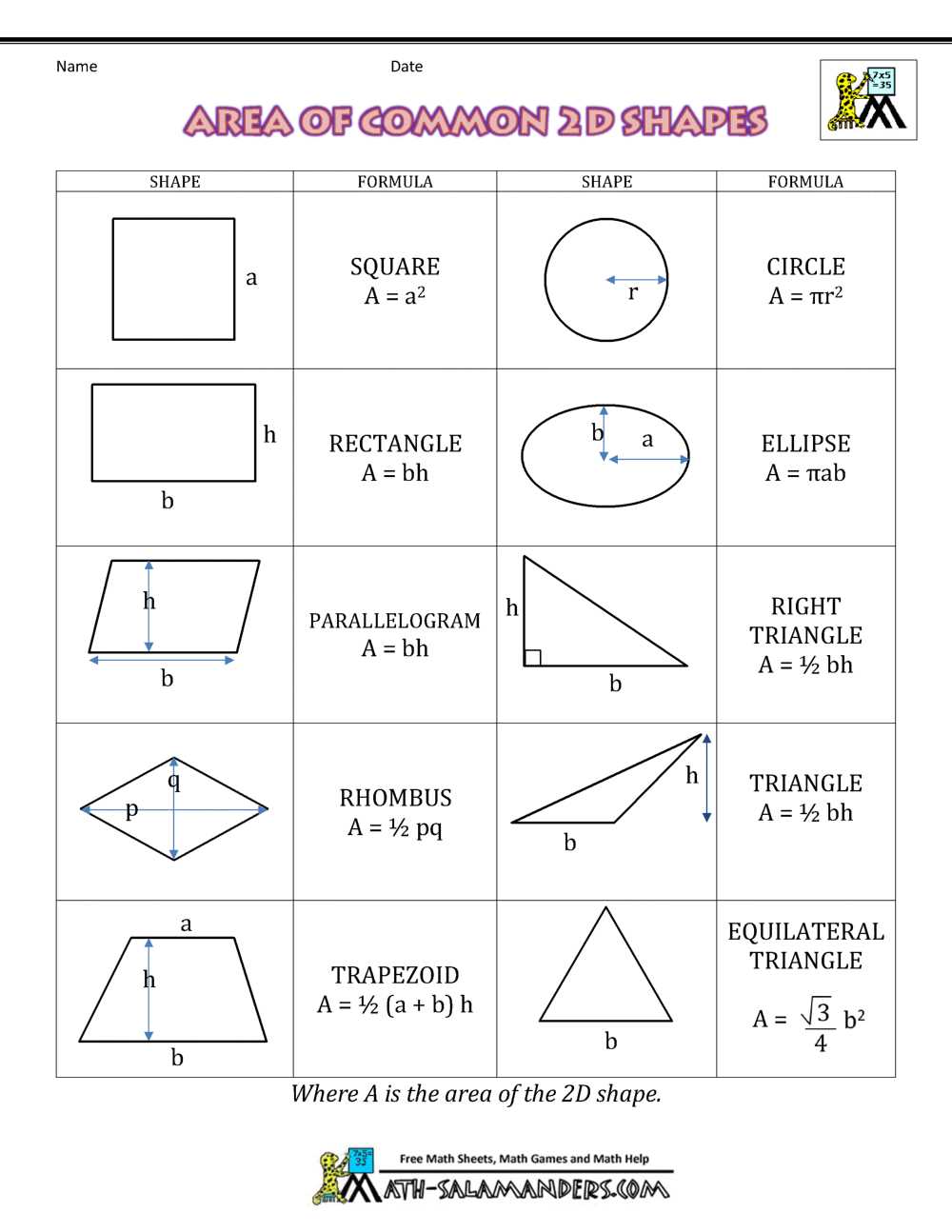
When calculating the area of triangles and quadrilaterals, it is important to understand the formulas and methods used. A triangle is a polygon with three sides and three angles, while a quadrilateral is a polygon with four sides and four angles.
The formula for finding the area of a triangle is to multiply the base by the height and divide the result by 2. The base is the length of one of the sides of the triangle, and the height is the distance from the base to the opposite vertex. For example, to find the area of a triangle with a base of 5 units and a height of 8 units, we can use the formula: Area = (5 * 8) / 2 = 20 square units.
Example:
- Triangle
- Base: 5 units
- Height: 8 units
- Area: (5 * 8) / 2 = 20 square units
The formula for finding the area of a quadrilateral depends on its shape. For rectangles and squares, the area can be calculated by multiplying the length of the base by the height. For example, to find the area of a rectangle with a length of 6 units and a height of 4 units, we can use the formula: Area = 6 * 4 = 24 square units.
Example:
- Rectangle
- Length: 6 units
- Height: 4 units
- Area: 6 * 4 = 24 square units
For other types of quadrilaterals, such as parallelograms and trapezoids, the area formula involves multiplying a base by the height. In these cases, the base is one of the sides of the quadrilateral, and the height is the distance between the base and its opposite side. Remember to use the appropriate formula for each shape to accurately calculate the area.
Area of Circles and Semi-Circles
The area of a circle is the amount of space enclosed within its boundaries. It is calculated by using the formula A = πr^2, where A represents the area and r represents the radius of the circle. The value of π is approximately 3.14, but it is important to use a more accurate value when performing calculations.
To find the area of a semi-circle, we can use the same formula as for a whole circle, but divide the result by 2. This is because a semi-circle is half of a circle. So, the formula becomes A = (πr^2)/2.
In order to calculate the area of circles and semi-circles, we need to know the value of the radius (or diameter) of the shape. The radius is the distance from the center of the circle to any point on its circumference. The diameter is the distance across the circle through its center, and it is equal to twice the length of the radius.
When working with mixed shapes, such as rectangles with circles or semi-circles attached, we can find the total area by adding the areas of each individual shape. For example, if a shape consists of a rectangle with a semi-circle attached to one of its sides, we can calculate the area of the rectangle using the formula A = length × width, and then calculate the area of the semi-circle using the formula mentioned earlier. Finally, we can add the two areas together to get the total area of the shape.
Understanding the concepts and formulas for calculating the area of circles and semi-circles is important in various fields, such as engineering, architecture, and mathematics. It allows us to accurately determine the amount of space occupied by these shapes and make informed decisions in real-life situations.
Finding the Area of Composite Shapes
When faced with a composite shape, which is made up of two or more simpler shapes, finding the total area can seem challenging at first. However, by breaking down the composite shape into simpler shapes and calculating the area of each individual shape, we can easily find the total area.
One approach to finding the area of a composite shape is to divide it into recognizable shapes such as rectangles, squares, triangles, and circles. By determining the area of each individual shape and then adding them together, we can find the total area. It is important to ensure that all the measurements (length, width, height, or radius) are known or can be determined through other measurements or formulas.
Another method to find the area of a composite shape is to break it down into smaller, non-overlapping shapes. For example, if the composite shape includes a rectangle and a triangle, we can find the area of each shape separately and then add them together. This method is especially useful when dealing with irregular or complex composite shapes that cannot be easily broken down into recognizable shapes.
Overall, finding the area of composite shapes requires breaking them down into simpler shapes, determining the area of each individual shape, and then adding them together. This can be done by recognizing recognizable shapes within the composite shape or by breaking it down into smaller, non-overlapping shapes. With these methods, finding the area of composite shapes becomes a manageable task.
Applying Area Calculations in Real-Life Examples
The concept of area calculations is not only important in mathematics, but it also has numerous practical applications in real-life scenarios. From construction to agriculture, understanding the area of various shapes is crucial in order to plan and execute projects efficiently. Let’s explore a few examples where area calculations play a significant role.
1. Construction:
When it comes to construction, accurate calculations of area are essential. Architects need to determine the area of the building’s footprint to ensure that it fits within the available space. Similarly, builders need to calculate the area of walls, floors, and ceilings to estimate the required materials, such as paint, tiles, or flooring. By accurately calculating the area, construction professionals can avoid unnecessary expenses and ensure the project’s success.
2. Farming:
In agriculture, area calculations are crucial for determining crop yields, planning irrigation systems, and managing land resources effectively. Farmers need to know the area of their fields to calculate the amount of fertilizer, seeds, and pesticides required. Additionally, knowing the area helps in planning irrigation methods to ensure proper water distribution. With accurate area calculations, farmers can optimize their resources and maximize their crop production.
- 3. Landscaping:
In the field of landscaping, area calculations play a significant role in designing outdoor spaces. Landscape architects need to calculate the area of lawns, flower beds, and other elements to determine the amount of grass, soil, or plants needed. They also need to calculate the area of walkways or patio spaces to estimate materials like pavers or concrete. By accurately assessing the area, landscape professionals can create visually appealing and functional outdoor environments.
These examples highlight just a few of the many real-life applications of area calculations. Whether it’s in construction, farming, or landscaping, understanding and applying area calculations is essential for successful project planning and execution.