The AP Statistics Chapter 6 Test is an important assessment that evaluates students’ understanding of various statistical concepts. In this test, students are expected to demonstrate their knowledge and skills in topics such as probability, random variables, and sampling distributions.
The test consists of a variety of questions, including multiple-choice, free response, and problem-solving. These questions are designed to assess students’ ability to apply statistical concepts to real-world situations and make informed decisions. It requires students to have a strong understanding of the fundamental principles of statistics, as well as the ability to analyze and interpret data.
Preparing for the AP Statistics Chapter 6 Test requires diligent studying and practice. Students should review the key concepts and formulas covered in the chapter, as well as complete practice problems and sample questions. They should also focus on understanding the underlying concepts and reasoning behind statistical methods, rather than simply memorizing formulas.
By carefully preparing for the AP Statistics Chapter 6 Test, students can improve their chances of success and demonstrate their mastery of statistical concepts. This test serves as an important benchmark in the AP Statistics course and can have an impact on students’ overall grades and future academic opportunities in the field of statistics.
Chapter 6: AP Statistics Test
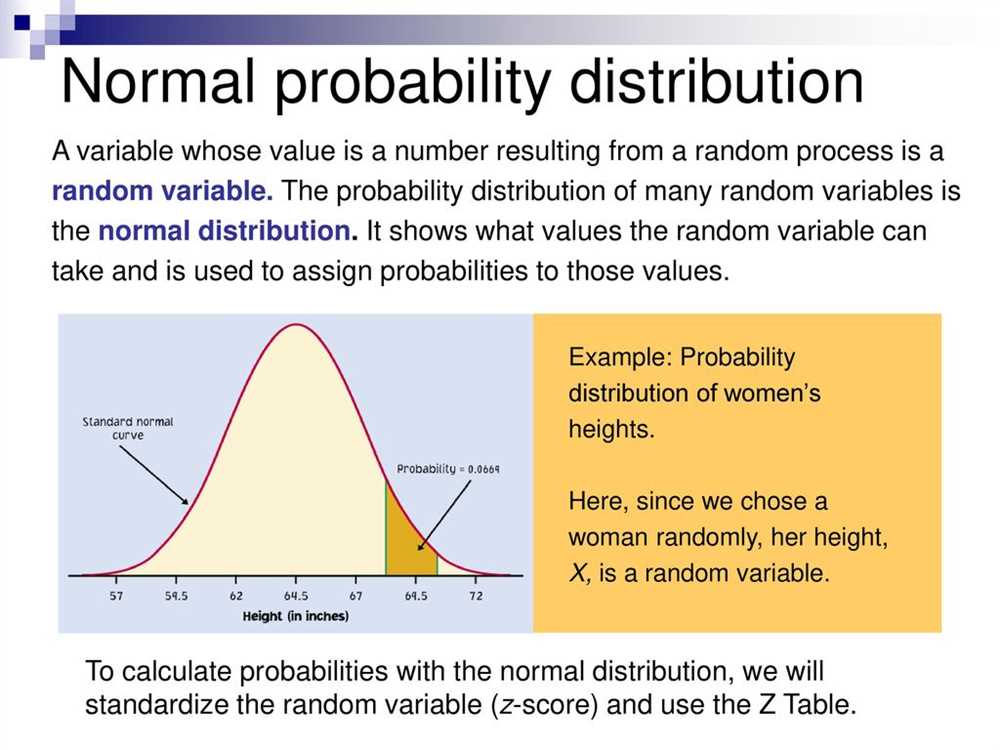
In Chapter 6 of AP Statistics, students learn about the concept of probability. This chapter focuses on understanding the basic principles of probability, calculating probabilities of different events, and exploring the relationship between probability and statistics. The AP Statistics test for Chapter 6 evaluates students’ comprehension and application of these concepts.
During the test, students are required to demonstrate their understanding of probability by analyzing various scenarios and calculating the probabilities of different outcomes. They may be asked to use theoretical probabilities, such as determining the probability of rolling a certain number on a fair die, or they may need to calculate empirical probabilities based on observed data.
The test may also assess students’ understanding of conditional probability and independence. Students may be asked to calculate conditional probabilities, determine if two events are independent or dependent, and interpret the results in the context of the problem. Additionally, the test may include questions on probability distributions, including the binomial distribution and the normal distribution.
Study Tips for the AP Statistics Chapter 6 Test:
- Review the basic principles of probability, such as the addition and multiplication rules.
- Practice calculating probabilities of different events using both theoretical and empirical approaches.
- Understand the concept of conditional probability and how it relates to independence.
- Revise the properties of probability distributions, such as mean, variance, and standard deviation.
- Work through practice problems and past AP Statistics questions to familiarize yourself with the types of questions that may appear on the test.
By thoroughly studying and understanding the concepts covered in Chapter 6, students can feel confident and prepared for the AP Statistics test. Reviewing the material, practicing calculations, and applying concepts to real-world scenarios will help students succeed in demonstrating their knowledge and skills in probability.
Overview of AP Statistics Chapter 6 Test
The AP Statistics Chapter 6 test focuses on the topic of probability. This chapter is an important part of the course as it introduces students to the fundamental concepts and principles of probability. It covers topics such as probability rules, conditional probability, independence, random variables, and probability distributions.
One of the key concepts covered in this chapter is probability rules. Students learn about the addition rule and the multiplication rule, which are used to calculate probabilities of different events. These rules help students understand how to combine probabilities in different scenarios.
The chapter also delves into conditional probability, which involves calculating the probability of an event given that another event has already occurred. Students learn to use conditional probability to solve problems and make predictions.
The concept of independence is another important topic covered in the chapter. Students learn how to determine whether two events are independent or dependent, and how to calculate probabilities in each case.
Furthermore, the chapter introduces students to the concept of random variables and probability distributions. Students learn how to define and calculate probabilities associated with different types of random variables, including discrete and continuous random variables. They also learn about probability distributions, such as the binomial and normal distributions, and how to use them to make predictions.
In summary, the AP Statistics Chapter 6 test examines students’ understanding of probability, including probability rules, conditional probability, independence, random variables, and probability distributions. It is essential for students to thoroughly grasp these concepts in order to perform well on the test and develop a strong foundation in statistics.
Understanding Sampling Distributions
A sampling distribution is a theoretical distribution that represents the probabilities associated with all possible sample statistics that could be obtained from a population. It is an important concept in statistics because it allows us to make inferences about a population based on a sample.
One key aspect of understanding sampling distributions is recognizing that they are based on the concept of repeated sampling. In other words, if we were to take multiple random samples from the same population and calculate a statistic (such as the mean or standard deviation) for each sample, the collection of these statistics would form the sampling distribution. This distribution helps us understand the variability and characteristics of the statistic being studied.
The shape of the sampling distribution depends on the underlying population distribution and the sample size. It is generally expected that as the sample size increases, the sampling distribution becomes more bell-shaped and symmetrical, resembling a normal distribution. This is known as the Central Limit Theorem, which states that for large enough sample sizes, the sampling distribution of the sample mean will be approximately normally distributed.
Sampling distributions are important for hypothesis testing and constructing confidence intervals. They allow us to determine the likelihood of observing a particular sample statistic, given the null hypothesis, and make decisions about the population based on this probability. Additionally, the standard error of the sampling distribution can be used to calculate confidence intervals, which provide a range of values that are likely to contain the true population parameter.
Key Concepts in Sampling Distributions
A sampling distribution is a distribution of all possible sample means or sample proportions that could be obtained from repeated sampling from a population. It is used to make inferences about a population based on a sample. Understanding the key concepts in sampling distributions is crucial for statistics, as it allows researchers to draw conclusions about populations without having to study every individual in the population.
Central limit theorem: One key concept in sampling distributions is the central limit theorem. This theorem states that the distribution of sample means or sample proportions approaches a normal distribution as the sample size increases, regardless of the shape of the population distribution. This is important because it allows researchers to make inferences about a population based on a small sample, knowing that the sampling distribution will still follow a normal distribution.
Standard error: Another important concept in sampling distributions is the standard error. The standard error measures the variability or spread of the sampling distribution. It is calculated as the standard deviation of the population divided by the square root of the sample size. The smaller the standard error, the more precise the sample estimate is likely to be.
Sampling distribution of the sample mean: The sampling distribution of the sample mean refers to the distribution of all possible sample means that could be obtained from repeated sampling. It is centered around the population mean and follows a normal distribution, as predicted by the central limit theorem. The standard error of the sample mean is a key factor in determining the width of the sampling distribution.
Sampling distribution of the sample proportion: Similarly, the sampling distribution of the sample proportion refers to the distribution of all possible sample proportions that could be obtained from repeated sampling. It is centered around the population proportion and follows a normal distribution, again thanks to the central limit theorem. The standard error of the sample proportion is calculated using the population proportion and the sample size.
By understanding these key concepts in sampling distributions, researchers can make reliable inferences about populations based on sample data. They can estimate population parameters, test hypotheses, and make predictions with a certain level of confidence, even when they are working with limited data.
The Central Limit Theorem
The Central Limit Theorem is a fundamental concept in statistics that states that for a large enough sample size, the distribution of the sample means approximates a normal distribution, regardless of the shape of the population distribution. This theorem is incredibly powerful and forms the basis for many statistical techniques and hypothesis testing.
One implication of the Central Limit Theorem is that even if the population is not normally distributed, the distribution of sample means will still be approximately normal. This allows statisticians to make inferences and draw conclusions about the population based on the sample data.
Another important concept related to the Central Limit Theorem is the standard error. The standard error of the sample mean is the standard deviation of the sample divided by the square root of the sample size. The standard error quantifies the variability of sample means and plays a crucial role in hypothesis testing and constructing confidence intervals.
The Central Limit Theorem has numerous practical applications. For example, it is often used in quality control to monitor the mean of a process by taking samples and calculating the sample mean. It is also used in survey sampling to estimate population parameters based on a sample. Additionally, the Central Limit Theorem is a foundational concept in hypothesis testing, where the distribution of sample means is compared to a known distribution to test a hypothesis.
In summary, the Central Limit Theorem provides a powerful tool for statisticians to analyze data and make inferences about populations. It allows for the use of normal distribution-based techniques, even when the population distribution is not normal. Understanding the Central Limit Theorem is crucial for any student or practitioner of statistics.
Hypothesis Testing with Sampling Distributions
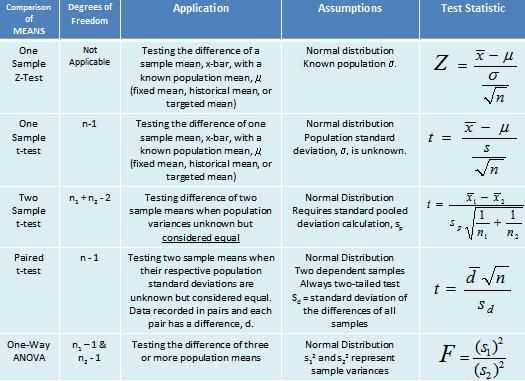
Hypothesis testing with sampling distributions is a statistical technique used to make inferences about a population based on a sample. It involves comparing the observed sample data to what is expected under a specific hypothesized population parameter value.
First, we define two competing hypotheses: the null hypothesis, denoted as H0, and the alternative hypothesis, denoted as Ha. The null hypothesis represents the status quo or the assumption that there is no difference or effect in the population parameter of interest. The alternative hypothesis, on the other hand, reflects the researcher’s belief or the claim being tested.
Next, we collect a random sample from the population and calculate a test statistic based on the sample data. This test statistic represents the discrepancy between the observed data and what is expected under the null hypothesis. The choice of the test statistic depends on the nature of the hypothesis being tested and the type of data collected.
Once we have the test statistic, we can determine its probability of occurrence assuming the null hypothesis is true. This probability is obtained by comparing the test statistic to the sampling distribution of the test statistic under the null hypothesis. If the obtained probability is very low (typically below a predetermined significance level), we reject the null hypothesis in favor of the alternative hypothesis. Otherwise, we fail to reject the null hypothesis.
Hypothesis testing with sampling distributions allows us to make objective decisions based on statistical evidence. It helps us assess the validity of claims, evaluate the impact of interventions or treatments, and make informed decisions in various fields such as medicine, economics, and social sciences.
Confidence Intervals and Sampling Distributions
In statistics, confidence intervals and sampling distributions play a crucial role in understanding the uncertainty associated with estimating population parameters based on sample data. By calculating a confidence interval, we can provide a range of plausible values for the parameter of interest, along with an associated level of confidence.
A confidence interval is calculated using a point estimate (such as the sample mean or proportion) and a margin of error. The margin of error is determined by the variability of the sample data and the desired level of confidence. For example, a 95% confidence interval means that if we were to repeat the sampling process multiple times, 95% of the resulting confidence intervals would contain the true population parameter.
The accuracy of confidence intervals relies on the properties of sampling distributions. A sampling distribution represents all possible sample statistics that could be obtained from repeated sampling of the same population. By assuming the sample is representative of the population, we can use the sampling distribution to make inferences about the population parameter of interest.
- Central Limit Theorem: The central limit theorem states that the distribution of sample means from a large sample will be approximately normal, regardless of the shape of the population distribution. This allows us to use the normal distribution to make inferences about population means.
- Standard Error: The standard error measures the variability of the sample means around the population mean. It is calculated by dividing the standard deviation of the population by the square root of the sample size. The standard error is used to estimate the standard deviation of the sampling distribution and is crucial in determining the margin of error for confidence intervals.
- T-Distribution: When the population standard deviation is unknown, the t-distribution is used instead of the normal distribution. The t-distribution has wider tails, which reflects the increased uncertainty associated with estimating the standard deviation based on a small sample.
In conclusion, confidence intervals and sampling distributions provide a framework for estimating population parameters and quantifying the uncertainty associated with those estimates. These concepts are fundamental in inferential statistics and allow researchers to draw conclusions about populations based on limited sample data.