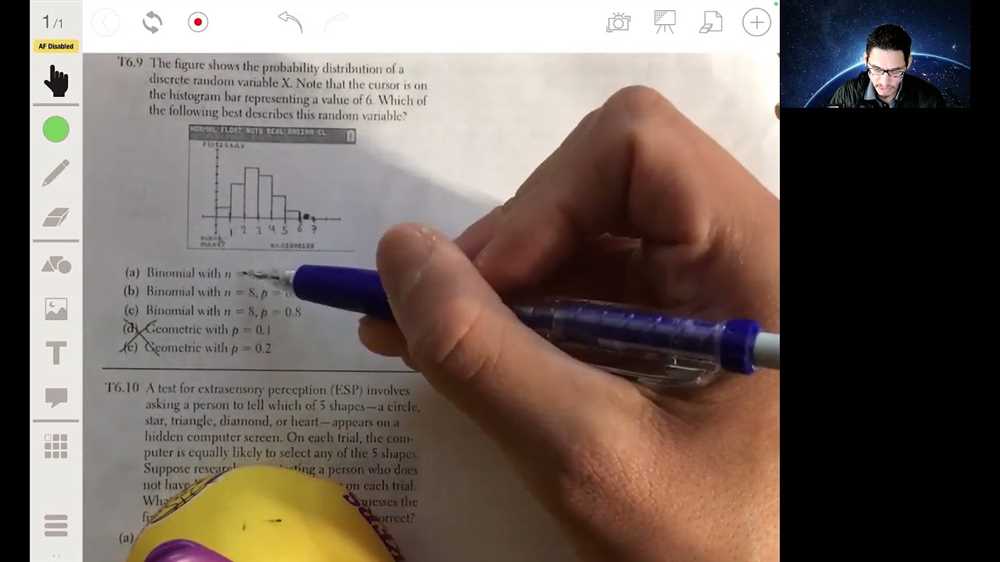
The AP Stats Chapter 3 Test is a comprehensive assessment that evaluates students’ understanding and application of key concepts in statistical analysis. This test serves as an important milestone in the AP Statistics course, as it covers essential topics such as probability, experimental design, and data analysis.
During this test, students will be challenged to demonstrate their knowledge of various statistical techniques, including constructing and interpreting confidence intervals, conducting hypothesis tests, and making informed decisions based on sample data. The test will not only assess their ability to perform these calculations but also their understanding of the underlying principles and the implications of their results.
Given the depth and breadth of the material covered in Chapter 3, the AP Stats test will require students to think critically and solve real-world statistical problems. They will need to apply their understanding of probability and sampling distributions to analyze data, make predictions, and draw conclusions. Additionally, students must be able to interpret and communicate their findings effectively, both verbally and in written form.
In preparation for the AP Stats Chapter 3 Test, students should review key concepts, practice solving problems, and familiarize themselves with common statistical terms and formulas. They should also strive to develop a strong understanding of the underlying concepts and how they relate to real-world situations. By mastering the material covered in Chapter 3, students will be well-equipped to tackle the test and excel in the AP Statistics course as a whole.
Understanding the Importance of AP Stats Chapter 3 Test
The AP Stats Chapter 3 test is a crucial assessment that evaluates students’ understanding of key statistical concepts and theories. This test plays a vital role in measuring students’ progress in the subject and is considered an important milestone in their AP Stats journey.
One of the primary reasons why the AP Stats Chapter 3 test is significant is because it covers fundamental topics that serve as building blocks for more complex statistical concepts. These topics include probability, random variables, probability distributions, and sampling distributions. Mastering these concepts is essential for students to grasp advanced statistical methods and theories in future chapters.
The AP Stats Chapter 3 test provides a comprehensive evaluation of students’ ability to apply statistical principles in real-world scenarios. It assesses their skills in interpreting and analyzing data, making inferences, and drawing valid conclusions. By testing their application of statistical methods, this assessment helps students develop critical thinking and problem-solving abilities, which are crucial in various fields such as business, medicine, and social sciences.
The test also serves as a benchmark to assess students’ overall understanding of the subject and their readiness for the AP Stats exam. Scoring well on the Chapter 3 test indicates a solid foundation in statistics, which can boost students’ confidence and motivation for further learning. Conversely, if students struggle with this test, it signals the need for additional practice and review to strengthen their comprehension of essential statistical concepts.
In conclusion, the AP Stats Chapter 3 test holds significance in assessing students’ knowledge and application of foundational statistical concepts. It plays a crucial role in measuring progress, preparing for future chapters, and evaluating overall readiness for the AP Stats exam. Therefore, understanding the importance of this test is essential for students aiming to excel in statistics and related fields.
What is AP Stats Chapter 3 Test?
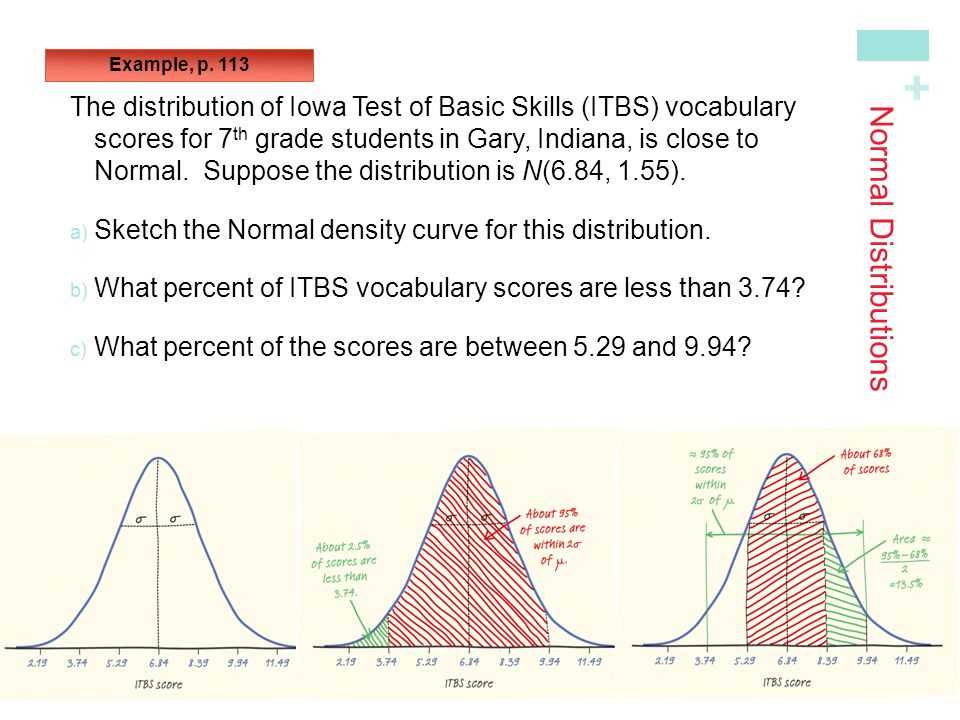
The AP Stats Chapter 3 Test is an assessment that evaluates students’ understanding of the concepts and skills covered in Chapter 3 of the AP Statistics curriculum. This test typically covers topics such as numerical summaries of data, including measures of center and spread, and interpreting and comparing distributions.
During this chapter, students learn about different types of data distributions, such as symmetric, skewed, and uniform distributions. They also study measures of center, such as mean and median, as well as measures of spread, like range and standard deviation. The test aims to assess students’ ability to apply these concepts to real-world scenarios and make data-driven decisions.
The AP Stats Chapter 3 Test may include multiple-choice questions, free-response questions, and problem-solving tasks. Students are expected to demonstrate their knowledge and understanding of statistical concepts, as well as their ability to analyze and interpret data. Effective preparation for the test involves reviewing class notes, completing practice problems, and seeking clarification on any challenging concepts.
Topics covered in the AP Stats Chapter 3 Test:
- Numerical summaries of data
- Different types of data distributions
- Measures of center
- Measures of spread
- Interpreting and comparing distributions
Tips for success:
- Review class notes and textbook materials
- Practice solving problems related to data distributions and numerical summaries
- Seek help or clarification on any challenging concepts
- Utilize online resources and practice tests to reinforce understanding
- Develop effective study strategies, such as creating flashcards or participating in study groups
- Take advantage of any review sessions or study guides provided by your instructor
- Manage your time effectively during the test and read each question carefully
- Show your work and provide clear explanations when required
- Check your answers for accuracy before submitting the test
By thoroughly preparing for the AP Stats Chapter 3 Test, students can demonstrate their proficiency in analyzing and interpreting data, and set themselves up for success in future statistical studies.
Why is AP Stats Chapter 3 Test Important?
The AP Stats Chapter 3 test is an important assessment for students studying statistics. This test covers various essential concepts and skills learned in Chapter 3 of the course. It serves as a way to evaluate the students’ understanding and proficiency in applying statistical methods such as organizing data, calculating measures of central tendency and variability, and interpreting graphical displays.
One of the key reasons why the AP Stats Chapter 3 test is important is that it enables students to demonstrate their ability to analyze and interpret data. By testing their skills in constructing and interpreting different types of graphs, such as dot plots, histograms, and box plots, the test assesses whether students can effectively communicate insights and conclusions drawn from data visualizations.
The AP Stats Chapter 3 test also plays a significant role in preparing students for future statistical analysis. The concepts covered in this chapter, including the properties of normal distributions and the empirical rule, form the foundation for more advanced statistical techniques. By successfully mastering the material and scoring well on the test, students build a strong base for tackling more complex topics in subsequent chapters and future statistical courses.
In summary, the AP Stats Chapter 3 test is important as it evaluates students’ understanding and application of statistical methods, their ability to interpret graphical displays, and prepares them for more advanced statistical analysis. By performing well on this test, students demonstrate their competence in fundamental statistics concepts and set themselves up for success in future statistical studies.
How Does AP Stats Chapter 3 Test Contribute to Overall Performance?
The AP Stats Chapter 3 test is a crucial assessment that plays a significant role in determining students’ overall performance in the AP Statistics course. This test focuses on the principles and concepts related to probability, including probability rules, conditional probability, and independence.
By testing students on Chapter 3 material, the AP Stats Chapter 3 test provides an opportunity to assess their understanding and application of key probability concepts. It evaluates their ability to analyze and interpret data in order to make informed decisions and predictions. This test not only measures knowledge retention but also assesses critical thinking skills and problem-solving abilities.
Key concepts covered in the AP Stats Chapter 3 test include:
- Probability rules: Students are expected to demonstrate an understanding of fundamental probability rules such as the addition rule, multiplication rule, and complement rule.
- Conditional probability: The test challenges students to calculate conditional probability and apply it in real-world scenarios.
- Independence: Students must understand the concept of independence and use it to determine whether events are independent or dependent.
Scoring well on the AP Stats Chapter 3 test is crucial for overall performance in the course. It showcases students’ mastery of key probability concepts, which are fundamental to understanding and analyzing data in statistics. A strong performance on this test indicates a solid foundation and prepares students for more advanced statistical concepts in later chapters and in the AP exam.
In summary, the AP Stats Chapter 3 test evaluates students’ knowledge of probability concepts and their ability to apply them. It serves as a significant contributor to overall performance by assessing critical thinking skills and problem-solving abilities. Scoring well on this test sets students up for success in the AP Statistics course and beyond.
Key Concepts Covered in AP Stats Chapter 3 Test
In AP Stats Chapter 3, students will encounter several key concepts related to experimental design, sampling methods, and bias. Understanding these concepts is crucial for a thorough understanding of statistics and data analysis. Some of the key concepts covered in this chapter include:
- Experimental Design: This concept focuses on the fundamental principles of designing and conducting experiments. Students will learn about the importance of random assignment, control groups, and replication in conducting valid experiments.
- Sampling Methods: This topic explores various sampling methods used to collect data from a population. Students will learn about simple random sampling, stratified sampling, cluster sampling, and systematic sampling. They will also understand the advantages and disadvantages of each method.
- Bias: Students will delve into the concept of bias and its impact on the validity of statistical analysis. They will learn about different types of bias, including selection bias, response bias, and nonresponse bias. Understanding bias is crucial in ensuring the accuracy and reliability of data analysis.
- Multistage Sampling: This concept introduces students to multistage sampling, a sampling technique used when a population is large or geographically dispersed. Students will learn about the steps involved in multistage sampling and how to obtain a representative sample using this method.
- Experimental Units and Variables: Students will understand the importance of defining the experimental units and variables in a statistical study. They will learn to identify the independent and dependent variables and how they relate to the research question or hypothesis.
- Randomization: Randomization plays a crucial role in experimental design, and students will learn about its significance in reducing bias and ensuring the validity of statistical conclusions. They will explore various randomization techniques and how to implement them in experiments.
These key concepts from AP Stats Chapter 3 form the foundation for further exploration of statistical analysis and inference. Mastering these concepts will enable students to apply them in real-world scenarios and make informed decisions based on data.
Sampling Distributions

In statistics, a sampling distribution is a probability distribution that describes the likelihood of various outcomes when a random sample is taken from a population. Understanding sampling distributions is crucial in statistical inference because it allows us to make predictions and draw conclusions about a population based on a sample.
When we take multiple random samples from the same population and calculate a statistic for each sample, the distribution of these statistics is called a sampling distribution. The shape of the sampling distribution depends on the size of the sample, the variability of the population, and the sampling method used.
Sampling distributions are important because they allow us to:
- Estimate population parameters using sample statistics.
- Evaluate the accuracy and precision of our estimates.
- Make inferences about the population based on the sample.
- Assess the probability of observing certain sample statistics.
One key concept in sampling distributions is the Central Limit Theorem (CLT). According to the CLT, when the sample size is large enough, the sampling distribution of the sample mean will be approximately normal, regardless of the shape of the population distribution. This allows us to make assumptions and perform hypothesis testing.
Overall, sampling distributions play a vital role in statistical analysis by providing a framework for making inferences about populations based on samples. By understanding the properties and characteristics of sampling distributions, we can make more informed decisions and draw accurate conclusions from our data.
Central Limit Theorem
The Central Limit Theorem (CLT) is a fundamental concept in statistics that states that the distribution of the sample mean approaches a normal distribution as the sample size increases, regardless of the shape of the population distribution. This theorem is of great importance as it allows us to make inferences about the population mean based on a sample mean.
The CLT is based on three key assumptions:
- The samples are randomly selected from the population.
- The sample size is large enough. Typically, a sample size of 30 or greater is considered sufficient.
- The observations within the sample are independent.
When these assumptions are met, the CLT tells us that the distribution of the sample mean will be approximately normally distributed with a mean equal to the population mean and a standard deviation equal to the population standard deviation divided by the square root of the sample size.
The Central Limit Theorem has numerous applications in statistical inference. It allows us to make confident statements about a population based on a sample, even if the population is not normally distributed. By calculating confidence intervals and performing hypothesis tests, we can estimate unknown population parameters with a certain level of confidence. The CLT is a cornerstone of statistical analysis and provides the foundation for many statistical techniques used in various fields such as business, economics, and social sciences.