
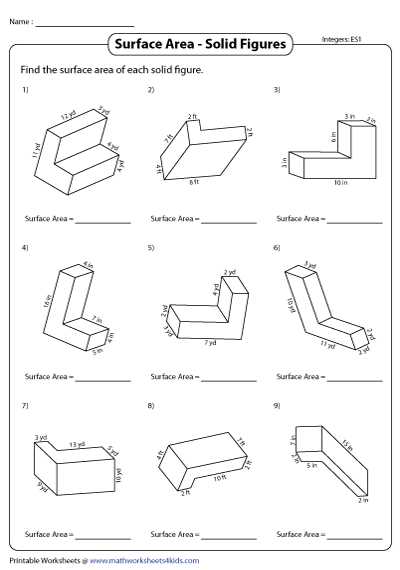
When studying geometry, it’s important to understand the concepts of areas and volumes of similar solids. These calculations are crucial in various mathematical and real-life applications, such as architecture, engineering, and physics. This article aims to provide a brief overview of the answers to the areas and volumes of similar solids worksheet.
One of the fundamental concepts in dealing with similar solids is the concept of similarity. Similar solids have the same shape, but their sizes may differ. The ratio of any corresponding lengths between two similar solids is constant. For example, if the ratio of the lengths of two similar solids is 1:2, then the ratio of their areas will be 1²:2² and the ratio of their volumes will be 1³:2³.
Using this concept, the worksheet may involve problems where students are asked to find the areas and volumes of similar solids given the measurements of one solid. This requires using the dimensions of the given solid and the given ratio to calculate the dimensions of the other solid. Once the dimensions are determined, the formulas for calculating the area and volume of the solid can be applied to find the answers.
It’s important for students to practice working with areas and volumes of similar solids to reinforce their understanding of the concepts. The worksheet answers provide a guide for students to check their work and ensure they are applying the correct formulas and calculations. By mastering these concepts, students will be better equipped to tackle more complex geometry problems and understand the practical applications of similar solids in the real world.
Objective of the Worksheet
The objective of the “Areas and Volumes of Similar Solids” worksheet is to assess students’ understanding of the concepts related to finding the areas and volumes of similar solids. This worksheet is designed to provide students with practice problems that require them to apply the formulas and concepts they have learned in class.
The worksheet includes a variety of problems that cover different aspects of finding areas and volumes of similar solids. Students will be required to calculate the area of different two-dimensional shapes, such as rectangles, triangles, and circles, as well as the volume of three-dimensional shapes, such as cubes, cylinders, and cones.
The worksheet also includes word problems that require students to analyze and interpret the given information to find the areas and volumes of similar solids in real-life scenarios. This will help students develop critical thinking skills and apply their knowledge in practical situations.
By completing this worksheet, students will improve their ability to understand and apply the formulas for finding the areas and volumes of similar solids. They will also enhance their problem-solving skills, as they will need to think critically and logically to solve the given problems. This worksheet will serve as a valuable tool for teachers to assess students’ mastery of the concept and identify areas where further instruction may be needed.
The Importance of Understanding Areas and Volumes of Similar Solids
When studying geometry, it is crucial to have a deep understanding of the concept of areas and volumes of similar solids. These mathematical calculations play a vital role in various fields such as architecture, engineering, physics, and even everyday life. By comprehending how to calculate and compare the sizes of similar solids, individuals can make informed decisions, solve problems, and create functional and aesthetically pleasing designs.
1. Design and Architecture: Architects and designers rely on their understanding of areas and volumes of similar solids to create visually appealing and structurally sound buildings. By accurately calculating the areas and volumes of similar shapes, architects can ensure that their designs meet building codes and regulations while maximizing usable space. From determining the size of rooms to estimating material requirements, these calculations are crucial in the design and construction processes.
2. Engineering and Construction: Engineers also heavily depend on areas and volumes of similar solids when designing and constructing structures such as bridges, tunnels, and dams. By correctly calculating the areas and volumes of similar shapes, engineers can determine load capacities, strength requirements, and materials needed for construction. Whether it’s designing the support system for a skyscraper or planning the layout of a highway interchange, understanding these calculations is essential for ensuring the safety and efficiency of engineering projects.
3. Manufacturing and Production: In the manufacturing industry, accurate measurements and calculations of areas and volumes of similar solids are crucial for product design, quality control, and production efficiency. From calculating material requirements for injection molding to determining storage capacities for containers, understanding these concepts enables manufacturers to optimize production processes and minimize waste. By accurately estimating the areas and volumes of similar shapes, manufacturers can ensure that their products meet specifications and are produced efficiently.
Overall, understanding areas and volumes of similar solids is crucial in various fields. Whether it’s designing buildings, engineering structures, or manufacturing products, accurate calculations of areas and volumes ensure efficiency, safety, and quality. Mastery of these mathematical concepts allows individuals to make informed decisions, solve problems, and contribute to the development of innovative and functional designs and solutions.
Definition of Similar Solids
In geometry, similar solids are three-dimensional figures that have the same shape, but not necessarily the same size. Two solids are considered similar if their corresponding angles are equal, and the ratios of their corresponding sides are proportional.
Similar solids can be thought of as scaled-up or scaled-down versions of each other. Just like similar triangles have proportional sides, similar solids have proportional lengths, areas, volumes, and surface areas.
Characteristics of Similar Solids
- Corresponding angles are equal
- Ratios of corresponding sides are proportional
- Proportional lengths: If the ratio of the lengths of corresponding sides of two similar solids is a:b, then the ratio of their volumes is a^3:b^3
- Proportional surface areas: If the ratio of the lengths of corresponding sides of two similar solids is a:b, then the ratio of their surface areas is a^2:b^2
Understanding the concept of similar solids is important in various mathematical and real-life applications. It allows us to compare and analyze different objects, determine their dimensions, and make predictions based on their similarity.
Furthermore, the properties of similar solids play a vital role in solving problems related to areas and volumes. By knowing the characteristics of similar solids, we can easily find the ratios of their areas or volumes, which helps in calculations and problem-solving.
Explanation of Similarity in Geometry
In geometry, similarity refers to the relationship between two figures that have the same shape but possibly different sizes. When two geometric figures are similar, their corresponding angles are equal, and the ratios of their corresponding sides are also equal. This concept is fundamental in understanding and solving problems involving areas and volumes of similar solids.
Similar triangles: One of the most common examples of similarity in geometry is similar triangles. Two triangles are similar if their corresponding angles are congruent, and the ratios of their corresponding side lengths are equal. This means that if you have two triangles with corresponding angles of 30°, 60°, and 90°, their side lengths will be in the same ratio of 1:2:√3, regardless of their size.
Ratio of areas and volumes: When two figures are similar, the ratio of their areas is equal to the square of the ratio of their corresponding side lengths. Similarly, the ratio of their volumes is equal to the cube of the ratio of their corresponding side lengths. This relationship allows us to find the areas and volumes of similar solids based on the given dimensions.
Applications: The concept of similarity is extensively used in various fields, such as architecture, engineering, and mapmaking. Architects use similarity to scale down or enlarge their designs while maintaining the same proportions. Engineers use similarity to model and analyze structures, such as bridges and buildings. Mapmakers use similarity to create accurate maps by scaling down large areas onto smaller sheets of paper.
Conclusion: Understanding similarity in geometry is crucial for solving problems involving areas and volumes of similar solids. Recognizing similar figures and applying the ratios of their corresponding side lengths allows us to find unknown dimensions and calculate the areas and volumes of similar shapes accurately.
Types of Similar Solids
Similar solids are three-dimensional shapes that have the same shape, but they may have different sizes. There are several types of similar solids, each with its own unique characteristics and properties.
1. Similar Rectangular Prisms
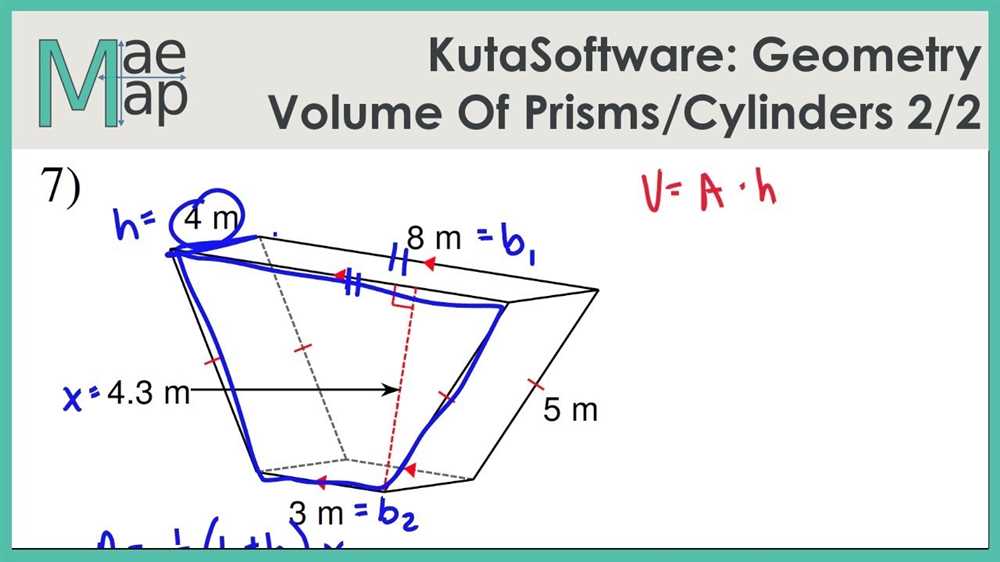
A rectangular prism is a solid shape with six rectangular faces. Similar rectangular prisms have the same shape, but their dimensions may be different. The corresponding sides of similar rectangular prisms are proportional to each other.
2. Similar Cylinders
A cylinder is a solid shape with two circular bases and a curved surface connecting the bases. Similar cylinders have the same shape, but their dimensions, such as the height and radius, may be different. The corresponding measurements of similar cylinders are proportional to each other.
3. Similar Pyramids
A pyramid is a solid shape with a polygonal base and triangular faces that meet at a common vertex. Similar pyramids have the same shape, but their dimensions, such as the height and base length, may be different. The corresponding measurements of similar pyramids are proportional to each other.
4. Similar Cones
A cone is a solid shape with a circular base and a curved surface that converges to a point called the vertex. Similar cones have the same shape, but their dimensions, such as the height and radius, may be different. The corresponding measurements of similar cones are proportional to each other.
In conclusion, similar solids come in various shapes and sizes, but they all share the characteristic of having the same shape. Recognizing and understanding the types of similar solids is important in solving problems related to their areas and volumes.
Determining the Scale Factor
When working with similar solids, determining the scale factor is an essential step in finding the relationship between their areas and volumes. The scale factor is the ratio of corresponding lengths or side lengths of two similar solids. It helps us understand how the size of one solid compares to another and allows us to calculate the areas and volumes of similar solids.
To determine the scale factor, we compare the corresponding lengths or side lengths of the two similar solids. For example, if we have two similar rectangular prisms, we would compare the lengths, widths, and heights of the two prisms. The ratio of these corresponding lengths gives us the scale factor.
Example:
We have two similar rectangular prisms. The length of the first prism is 6 units, and the length of the second prism is 12 units. The scale factor between the two prisms can be calculated as:
- Scale factor = Length of second prism / Length of first prism
- = 12 units / 6 units
- = 2
In this example, the scale factor is 2, which means that the second prism is twice as long as the first prism. This scale factor can be used to calculate the areas and volumes of the two similar solids by applying the appropriate formulas and multiplying them by the scale factor.
Determining the scale factor is crucial in understanding the relationship between the areas and volumes of similar solids. It helps us compare their sizes and calculate the corresponding measurements accurately.
Formula for Calculating the Scale Factor
The scale factor is an important concept when it comes to calculating the areas and volumes of similar solids. It represents the ratio of any two corresponding lengths in similar figures. The scale factor can be calculated using the formula:
Scale Factor = Length of side in the second figure / Length of side in the first figure
This formula allows us to find the scale factor when the lengths of corresponding sides are known. It is essential to use the correct lengths from the corresponding sides to ensure accurate calculations.
For example, let’s consider two similar rectangular prisms. The length of the corresponding sides in the first prism is 8 units, and in the second prism, it is 12 units. By applying the formula, we can find the scale factor:
Scale Factor = 12 units / 8 units = 1.5
The scale factor in this case is 1.5. This means that the second prism is 1.5 times larger than the first prism in terms of length.
The scale factor is a crucial tool in solving problems related to areas and volumes of similar solids. It helps in understanding the relationship between different measurements in similar figures and allows for accurate calculations.
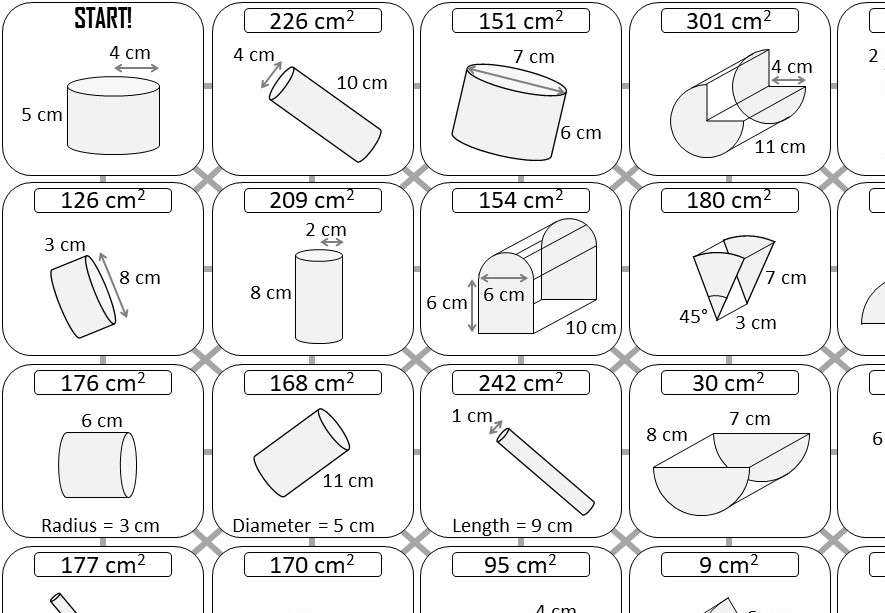
Example Problems with Solutions
Here are some example problems with solutions to help you practice finding the areas and volumes of similar solids:
Problem 1:
Find the surface area of a cube with side length 5 cm.
Solution:
To find the surface area of a cube, we need to find the area of each face and then add them together. Since a cube has all faces congruent, we can just find the area of one face and multiply it by 6. The area of a square is found by multiplying the length of one side by itself, so the area of one face is 5 cm * 5 cm = 25 cm2. Therefore, the surface area of the cube is 6 * 25 cm2 = 150 cm2.
Problem 2:
Find the volume of a rectangular prism with length 6 cm, width 4 cm, and height 3 cm.
Solution:
The volume of a rectangular prism is found by multiplying its length, width, and height together. So the volume of this rectangular prism is 6 cm * 4 cm * 3 cm = 72 cm3.
Problem 3:
Find the surface area of a cylinder with radius 2 cm and height 5 cm.
Solution:
The surface area of a cylinder is found by adding the areas of its two bases (circles) and the area of its lateral surface (rectangle). The area of a circle is found by multiplying pi (approximately 3.14) by the square of its radius, so the area of one base is 3.14 * (2 cm)^2 = 12.56 cm2. The area of the lateral surface is found by multiplying the circumference of the base (2 * pi * radius) by the height, so the area of the lateral surface is 2 * 3.14 * 2 cm * 5 cm = 62.8 cm2. Therefore, the total surface area of the cylinder is 2 * 12.56 cm2 + 62.8 cm2 = 87.92 cm2.
These examples should help you understand how to find the areas and volumes of similar solids. Remember to carefully consider the formulas and units when solving these types of problems.