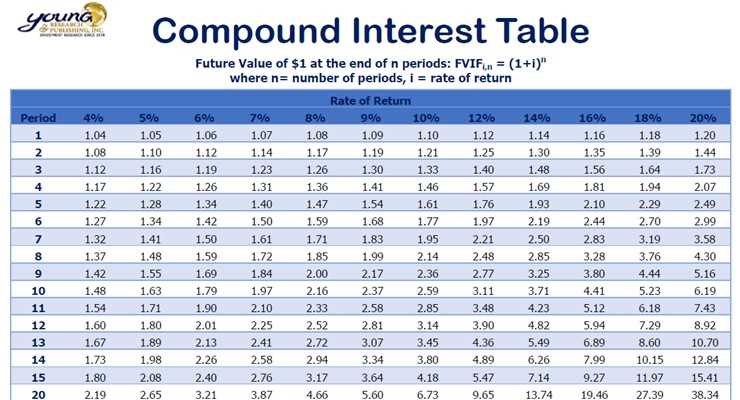
Understanding compound interest is crucial for financial planning and investment decisions. In Section 5 of the compound interest lesson, we will explore the answer key and delve deeper into the calculations involved in determining the final amount of an investment or loan.
The compound interest formula, A = P(1 + r/n)^(nt), may seem complex at first, but breaking it down step by step can simplify the process. We will discuss the meaning of each variable and how it affects the overall outcome.
One key aspect we will focus on is the concept of compounding periods. Depending on the frequency of interest accrual, compounding can occur annually, semi-annually, quarterly, or even monthly. We will examine how different compounding frequencies impact the final amount and the significance of selecting the most suitable option.
Moreover, the compound interest formula allows for variations in interest rates and time periods. By adjusting these parameters, we can calculate the potential growth of an investment or the total repayment amount for a loan. We will explore different scenarios and provide examples to help solidify your understanding of the calculations involved.
By the end of Section 5, you will have a comprehensive understanding of compound interest and how to utilize the answer key effectively. Armed with this knowledge, you will be better equipped to make informed financial decisions and harness the power of compound interest to your advantage.
Section 5.5 Compound Interest Answer Key
Compound interest is a powerful financial concept that allows individuals and businesses to earn interest on both their initial investment and the interest that accumulates over time. In Section 5.5 of the textbook, students are introduced to various formulas and concepts related to compound interest. The answer key provided for this section enables students to check their understanding and accuracy of their calculations.
The answer key includes step-by-step solutions to the examples and practice problems presented in Section 5.5. It helps students verify if they are correctly applying the compound interest formula, which involves principal amount, interest rate, time, and number of compounding periods. By referring to the answer key, students can identify any errors or misconceptions they may have in their calculations and seek clarification from the instructor if needed.
The answer key also provides additional information and explanations to further enhance students’ comprehension of compound interest. It covers essential concepts such as compounding frequency, nominal annual interest rate, effective annual interest rate, and applications of compound interest in real-life situations. Students can use the answer key as a resource for further study and to deepen their understanding of compound interest and its practical implications.
Overall, the Section 5.5 Compound Interest Answer Key serves as a valuable tool for students to assess their understanding and practice their skills in calculating compound interest. It provides a comprehensive guide to solving problems and offers additional explanations to reinforce concepts. By utilizing the answer key, students can ensure their accuracy and mastery of compound interest calculations, thereby building a solid foundation for their financial literacy.
Understanding Compound Interest
Compound interest is a concept that plays a significant role in finance and investing. It refers to interest that is calculated not only on the initial principal but also on the accumulated interest over time. This means that as time progresses, the interest earned on an investment or loan increases.
One key factor in understanding compound interest is the compounding period. This refers to how often interest is added to the principal. The more frequently interest is compounded, the greater the potential for exponential growth in the investment. For example, if interest is compounded annually, the interest earned will be added to the principal once a year. However, if interest is compounded quarterly, the interest is added every three months, resulting in more frequent compounding and higher overall returns.
It is important to note that compound interest can work both for and against you. When investing, compound interest can be your ally, as it allows your initial investment to grow steadily over time. However, when borrowing, compound interest can work against you, as it increases the total amount you owe over time.
To calculate compound interest, you need to know the initial principal, the interest rate, the compounding period, and the time period of the investment or loan. Using these variables, you can use various formulas or online calculators to determine the final amount and the interest earned.
Summary:

- Compound interest refers to interest that is calculated on the initial principal as well as the accumulated interest over time.
- The compounding period determines how often interest is added to the principal.
- Compound interest can work both for and against you, depending on whether you are investing or borrowing.
- To calculate compound interest, you need to know the initial principal, interest rate, compounding period, and time period.
Compound Interest Formula

Compound interest is a concept in finance that refers to the process of earning interest on both the original amount of money invested (known as the principal) and the accumulated interest from previous periods. It is an essential concept for understanding how investments grow over time and is commonly used in various financial calculations.
The compound interest formula allows us to calculate the future value of an investment by incorporating the interest rate, the number of compounding periods, and the initial investment. The formula is as follows:
A = P(1 + r/n)nt
where:
- A is the future value of the investment
- P is the principal (initial investment)
- r is the annual interest rate (expressed as a decimal)
- n is the number of compounding periods per year
- t is the number of years
By plugging in the values for the variables in the compound interest formula, we can calculate the future value of an investment after a certain period of time. This formula takes into account the compounding effect, which means that the interest earned in each compounding period gets added to the principal, resulting in a higher total amount of interest earned over time.
The compound interest formula is widely used in financial planning, investment analysis, and banking. It allows individuals and businesses to determine the potential growth of their investments and make informed decisions about where to allocate their funds. Understanding the concept of compound interest and how to apply the formula is crucial for intelligent financial management and wealth accumulation.
Solving Compound Interest Problems
Compound interest is a powerful concept that allows us to calculate the growth of money over time. When dealing with compound interest problems, it’s important to understand the key components involved and how to apply the appropriate formulas.
Firstly, we need to determine the principal amount or the initial amount of money that is invested. This is the starting point for our calculations. Next, we need to know the interest rate, which represents the percentage of interest that is earned or charged on the principal. The interest rate can be stated either as an annual rate or a rate over a different period, such as per month or per quarter.
Another crucial factor in compound interest problems is the time period or the number of compounding periods involved. Compounding periods can be annually, semi-annually, quarterly, monthly, or even daily. The frequency of compounding determines how often the interest is applied to the principal. The more frequent the compounding, the faster the growth of the money.
To solve compound interest problems, we can use the formula A = P(1 + r/n)^(nt), where A is the final amount, P is the principal, r is the interest rate, n is the number of compounding periods per year, and t is the number of years. By plugging in the known values and solving for the unknown, we can find the final amount.
It’s important to pay attention to the units of time and interest rate used in the problem and adjust them accordingly to ensure accurate calculations. Additionally, rounding to the appropriate number of decimal places is necessary to maintain precision in the final answer. By understanding the components and applying the compound interest formula correctly, we can solve compound interest problems effectively and make informed financial decisions.
Calculating Compound Interest with Different Compounding Periods
The calculation of compound interest can vary based on the frequency at which interest is compounded. When interest is compounded annually, the interest is added to the initial amount once a year. However, in some cases, interest may be compounded more frequently, such as semiannually, quarterly, or monthly.
When interest is compounded more frequently, the interest is added to the initial amount more often throughout the year, resulting in a higher effective interest rate. To calculate the compound interest with different compounding periods, the formula needs to be adjusted accordingly.
For example, if the interest is compounded semiannually, the formula would be: A = P(1 + r/n)^(nt), where A is the final amount, P is the principal amount, r is the annual interest rate, n is the number of times interest is compounded per year, and t is the number of years.
It is important to note that as the compounding period increases, the effective interest rate also increases. This means that for the same principal and annual interest rate, the final amount will be higher when the interest is compounded more frequently. It is beneficial to understand the compounding frequency when comparing different investment options or when calculating the growth of savings over time.
Finding the Principal Amount
When calculating compound interest, it is often necessary to find the principal amount, or the initial investment or loan amount. This can be done using the compound interest formula, which takes into account the interest rate, the number of compounding periods, and the final amount.
To find the principal amount, we can rearrange the compound interest formula to solve for P:
P = A / (1 + r/n)nt
Where P represents the principal amount, A is the final amount, r is the interest rate, n is the number of compounding periods per year, and t is the number of years the money is invested or borrowed for.
By plugging in the values for A, r, n, and t, we can calculate the principal amount. It is important to note that the interest rate, number of compounding periods, and number of years must be consistent with how the interest is compounded. For example, if the interest is compounded annually, the interest rate and number of compounding periods should be based on a yearly basis.
Calculating the principal amount is crucial in financial planning and decision-making. By knowing the principal amount, individuals and businesses can determine the initial investment or loan required to achieve a specific final amount, taking into account the interest rate and compounding frequency. This knowledge enables informed financial choices and helps ensure sound financial growth and stability.
Finding the Rate of Interest

When it comes to calculating compound interest, one of the most important factors to consider is the rate of interest. The rate of interest determines how much your initial investment will grow over time, and it plays a crucial role in determining your overall returns. Finding the rate of interest can be a bit tricky, but with the right formulas and calculations, you can determine it accurately.
The first step in finding the rate of interest is to gather all the necessary information. You will need to know the initial principal amount, the final amount, and the time period for which the investment is made. Additionally, you will need to know whether the interest is compounded annually, semi-annually, quarterly, or monthly. Once you have all this information, you can move on to the next step.
To find the rate of interest, you can use the compound interest formula: A = P(1 + r/n)^(nt). Here, A represents the final amount, P is the principal amount, r is the rate of interest as a decimal, n is the number of times the interest is compounded per year, and t is the time period in years. By rearranging this formula and solving for r, you can find the rate of interest.
Another way to find the rate of interest is by using a financial calculator or an excel sheet with built-in formulas. These tools allow you to input the initial and final amounts, the time period, and the compounding frequency, and they will automatically calculate the rate of interest for you. This can be a quicker and more convenient method, especially if you are dealing with complex calculations or multiple investments.
Finding the Time Period
When calculating compound interest, one of the key variables to determine is the time period. The time period refers to the length of time for which the interest is being calculated and can have a significant impact on the overall amount earned or owed.
To find the time period, it is important to know the interest rate, the principal amount, and the final amount. The interest rate is expressed as a percentage and represents the rate at which the investment or loan is growing. The principal amount is the initial amount of money invested or borrowed, while the final amount is the total amount after the interest has been added or deducted.
Using these three variables, the formula to find the time period is: time = log(final amount / principal amount) / log(1 + interest rate). This formula is derived from the compound interest formula, which takes into account the exponential growth of the investment or loan over time.
By plugging in the values for the final amount, principal amount, and interest rate into the formula, it is possible to calculate the time period. This can be useful for individuals who want to know how long it will take for their investment to grow to a certain amount or for borrowers who want to determine how long it will take to pay off a loan.
It is also important to note that the time period can be expressed in different units, such as years, months, or days, depending on the specific context of the calculation. For example, if the interest rate is given on an annual basis, the time period will be in years. However, if the interest rate is given on a monthly basis, the time period will be in months.
In conclusion, finding the time period is an essential step in calculating compound interest. By using the formula and plugging in the appropriate values, individuals can determine how long it will take for their investment to grow or how long it will take to pay off a loan.