
If you are a student studying statistics or preparing for a test, then you have probably come across Chapter 5 in your textbook, which focuses on various statistical concepts and techniques. Understanding the material covered in this chapter is essential for any student looking to gain a solid foundation in statistics. In order to assess your knowledge and skills, your instructor may assign you an Ap stats ch 5 test to see how well you have grasped the concepts and are able to apply them in real-world scenarios.
The Ap stats ch 5 test is designed to challenge you and push you to think critically about statistics. It may cover topics such as probability, random variables, probability distributions, and sampling distributions. These concepts are fundamental to understanding statistics and are often used in various fields such as business, economics, social sciences, and more.
Preparing for the Ap stats ch 5 test requires a solid understanding of the material covered in Chapter 5. You should review your textbook, notes, and any additional resources provided by your instructor. Practice problems and sample questions can also be helpful in reinforcing your understanding and identifying areas where you may need additional study. Taking the time to thoroughly prepare for the test will not only help you earn a good grade but will also enhance your overall understanding of statistics.
What to Expect for Your AP Stats Ch 5 Test
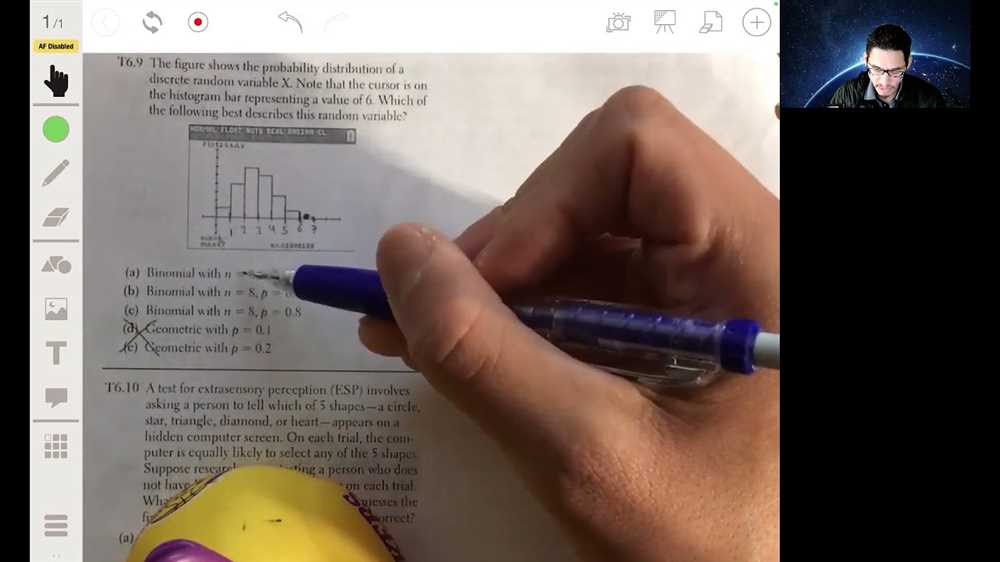
As you prepare for your AP Stats Ch 5 test, it’s important to have a clear understanding of the topics that will be covered and what you can expect. This chapter focuses on the concepts of probability and random variables, so be sure to review these thoroughly before the test.
Probability: Expect to encounter questions that test your understanding of basic probability rules, such as the addition and multiplication rules. You may also be asked to calculate probabilities using tree diagrams and combinations. Additionally, be prepared to apply these concepts to real-life scenarios and analyze data from probability distributions.
Discrete Random Variables: Another key topic on the test will be discrete random variables. You should be familiar with the probability mass function (PMF) and cumulative distribution function (CDF) for discrete random variables. You may also need to calculate expected values, variances, and standard deviations for discrete random variables.
Continuous Random Variables: The test may also include questions related to continuous random variables. It’s essential to understand the probability density function (PDF) and cumulative distribution function (CDF) for continuous random variables. You may be asked to find probabilities using these functions or calculate expected values, variances, and standard deviations for continuous random variables.
Sampling Distributions: Expect to encounter questions that assess your knowledge of sampling distributions, such as the sampling distribution of the mean and sampling distribution of the proportion. You may be asked to use these distributions to make inferences about population parameters or calculate confidence intervals.
Statistical Inference: Finally, be prepared to apply statistical inference techniques such as hypothesis testing and confidence intervals. You should be comfortable interpreting hypothesis tests, calculating p-values, and using confidence intervals to estimate population parameters.
Overall, it’s crucial to study and review these concepts thoroughly before your AP Stats Ch 5 test. Make sure you understand the key principles and formulas and are able to apply them to both theoretical and real-world situations. Good luck!
Understanding Probability and Random Variables
The concept of probability is essential in statistics as it helps in understanding the likelihood of different events occurring. Probability is a way to quantify uncertainty and provides a framework for making predictions and analyzing data. By studying probability, statisticians can make informed decisions and draw conclusions based on the likelihood of certain outcomes.
A random variable is a key concept in statistics that represents the numeric outcome of a random event. It is a function that assigns a real number to each outcome of a random experiment. Random variables can be discrete, taking on values from a countable set, or continuous, taking on values from an interval. Random variables allow statisticians to model and analyze complex systems by assigning probabilities to different outcomes.
When working with probability, it is important to understand the fundamental principles and rules that govern its calculations. The law of large numbers states that as the number of trials or observations increases, the observed frequency of an event will converge to its true probability. This principle is the basis for estimating probabilities based on observed data.
Additionally, the concept of independence is crucial in probability. Two events are considered independent if the occurrence or non-occurrence of one event does not affect the likelihood of the other event. This concept allows for the calculation of joint probabilities, where the probability of two or more events occurring simultaneously is determined.
In summary, understanding probability and random variables is vital for conducting statistical analyses and making informed decisions based on data. Probability allows statisticians to quantify uncertainty, while random variables provide a way to represent the outcomes of random events. By applying probability principles and understanding concepts like independence, statisticians can make accurate predictions and draw meaningful conclusions from data.
Exploring Probability Distributions
A probability distribution is a mathematical function that describes the likelihood of different outcomes in an experiment or random event. It provides a way to quantify and analyze uncertainty by assigning probabilities to each possible outcome.
There are two main types of probability distributions: discrete and continuous. Discrete distributions are used when the possible outcomes are countable and have specific values, such as the number of heads obtained when flipping a coin. Continuous distributions are used when the possible outcomes can take on any value within a range, such as the height of individuals in a population.
Discrete Probability Distributions:
- A probability mass function (PMF) is used to describe the probabilities of all possible values that a discrete random variable can take. It assigns a probability to each possible outcome.
- Common examples of discrete probability distributions include the binomial distribution, which models the number of successes in a fixed number of independent Bernoulli trials, and the Poisson distribution, which models the number of events occurring in a fixed interval of time or space.
Continuous Probability Distributions:
- A probability density function (PDF) is used to describe the probability of a continuous random variable falling within a particular range of values. Unlike a PMF, it does not assign probabilities to specific outcomes, but rather gives the probability density at each point on the real line.
- Common examples of continuous probability distributions include the normal distribution, which is often used to model real-valued random variables, and the exponential distribution, which models the time between events occurring at a constant rate.
By understanding and exploring probability distributions, statisticians can analyze data and make predictions with greater accuracy and precision. Different distributions have different shapes and characteristics, which can provide insights into the underlying processes generating the data. This knowledge can be applied in various fields, such as finance, engineering, and healthcare, to make informed decisions and solve real-world problems.
Mastering Discrete Random Variables
A discrete random variable is a variable that can take on only a finite or countably infinite number of possible values. In statistics, it is important to understand the properties and characteristics of discrete random variables in order to analyze and interpret data effectively.
Probability distribution is a fundamental concept in the study of discrete random variables. It provides a systematic way to assign probabilities to each possible value of the random variable. The probability distribution is often represented using a probability mass function (PMF), which assigns a probability to each possible value.
One key property of a discrete random variable is its expected value, also known as the mean. The expected value is a measure of the center of the distribution and represents the average value the random variable is likely to take on. It is calculated by multiplying each possible value of the random variable by its corresponding probability and summing them up.
Another important property is the variance of a discrete random variable, which measures the spread or variability of the distribution. The variance is calculated by taking the difference between each possible value of the random variable and the expected value, squaring it, multiplying by its corresponding probability, and summing them up. The standard deviation is the square root of the variance.
Understanding and mastering discrete random variables is essential for making accurate statistical inferences and drawing meaningful conclusions from data. By analyzing the probability distribution, expected value, and variance, statisticians can gain insights into the characteristics and behavior of the random variable, allowing for sound decision-making and hypothesis testing.
Understanding Continuous Random Variables
A continuous random variable is a variable that can take on any value within a certain range or interval. Unlike discrete random variables, which can only take on specific values, continuous random variables can take on any value within their range. Examples of continuous random variables include measurements such as height, weight, time, and temperature.
One key concept in understanding continuous random variables is the probability density function (PDF). The PDF is a function that describes the likelihood of a random variable taking on a specific value. It is often represented graphically as a curve, where the area under the curve represents the probability of the variable falling within a certain interval. The area under the entire curve is always equal to 1.
When working with continuous random variables, we often calculate probabilities by finding the area under the curve using integration. This allows us to determine the probability of a variable falling within a certain range or interval. For example, we can use the PDF of a normal distribution to calculate the probability of a person’s height falling within a certain range.
Another important concept in understanding continuous random variables is the cumulative distribution function (CDF). The CDF is the integral of the PDF and represents the probability that the random variable is less than or equal to a specific value. By evaluating the CDF at a given value, we can determine the probability of the variable being less than or equal to that value.
In summary, understanding continuous random variables involves grasping the concepts of the probability density function and the cumulative distribution function. These functions allow us to calculate probabilities and make inferences about the likelihood of a variable falling within a certain range or interval. Continuous random variables are essential in many areas of statistics, particularly when dealing with measurements and real-life data.
Calculating Expected Values and Variance
In the field of statistics, calculating expected values and variance is an essential component of analyzing data. Expected values help us understand the average or typical outcomes of a random process, while variance measures the spread or dispersion of those outcomes.
To calculate the expected value of a random variable, we multiply each possible outcome by its corresponding probability, and then sum up the products. This gives us an estimation of the long-term average outcome we can expect to observe. The formula for expected value is: E(X) = (x1 * P(x1)) + (x2 * P(x2)) + … + (xn * P(xn)), where x1, x2, …, xn are the possible outcomes with respective probabilities P(x1), P(x2), …, P(xn).
Variance, on the other hand, measures the variability or dispersion of the values around the expected value. It is calculated by taking the squared difference between each outcome and the expected value, multiplying it by the probability of that outcome, and summing up these products. The formula for variance is: Var(X) = ( (x1 – E(X))^2 * P(x1) ) + ( (x2 – E(X))^2 * P(x2) ) + … + ( (xn – E(X))^2 * P(xn) ). The square root of the variance, known as the standard deviation, provides a measure of the average distance of the outcomes from the expected value.
These calculations are particularly useful in various statistical applications, such as hypothesis testing, regression analysis, and decision making. By understanding the expected values and variance of a random variable, statisticians and researchers can make informed predictions, evaluate the significance of observed differences, and assess the reliability of their findings.
Interpreting Standard Deviation and Z-Scores
The standard deviation is a measure of the variation or spread of data. It tells us how much the individual data points deviate from the mean. A larger standard deviation indicates a greater amount of variability or dispersion, while a smaller standard deviation indicates less variability. For example, if the standard deviation of a test score distribution is 10, it means that most scores are within 10 points of the average score.
Z-scores, also known as standardized scores, measure how many standard deviations a particular data point is from the mean. A positive z-score indicates that the data point is above the mean, while a negative z-score indicates that it is below the mean. Z-scores can be used to compare and interpret data points from different distributions. For example, if a student’s z-score on a standardized test is 2, it means that their score is two standard deviations above the average score.
Interpreting standard deviation and z-scores is crucial in statistical analysis. They provide important information about the distribution of data and allow us to compare individual data points to the overall distribution. By understanding the standard deviation and z-scores, we can make informed decisions and draw meaningful conclusions from our data.