
If you’ve ever struggled with understanding set notation and interval notation, you’re not alone. Many students find these topics confusing and overwhelming. That’s why it’s important to have a clear understanding of these concepts and practice applying them to various problems.
In this article, we will provide you with the answers to a set and interval notation worksheet. By going through these answers, you will be able to see how the concepts of set notation and interval notation are used in solving different types of problems.
Set notation is a way of representing a set of numbers or objects. It uses braces {} to enclose the elements of the set. For example, the set of even numbers can be represented as {2, 4, 6, 8, …}. Interval notation, on the other hand, represents a range of numbers with the use of parentheses () or brackets []. For example, the interval (0, 10) represents all the numbers between 0 and 10, excluding both 0 and 10.
By understanding and mastering set notation and interval notation, you will be able to solve a wide range of mathematical problems, including inequalities, absolute value equations, and more. So let’s dive into the answers to the set and interval notation worksheet and strengthen our understanding of these concepts!
Set and Interval Notation Worksheet Answers

Set and interval notation is an important topic in mathematics, particularly in the field of algebra. It allows us to represent sets of numbers or intervals on the number line using concise and standardized notation. Understanding how to interpret and work with set and interval notation is crucial for solving mathematical problems and communicating mathematical ideas.
When working with a set of numbers, it is common to use set notation, which is represented by braces {}. For example, the set of all even numbers can be written as {2, 4, 6, 8, …}. Interval notation, on the other hand, represents a range of numbers and is often used to describe intervals on the number line. For instance, the interval (0, 5) represents all real numbers between 0 and 5, excluding both endpoints.
In order to effectively solve problems involving sets and intervals, it is important to be able to convert between set notation and interval notation. For example, if we are given the set {x | -3 ≤ x < 7} in set notation, we can rewrite it in interval notation as [-3, 7). This means that x can take on any value between -3 and 7, including -3 but excluding 7.
Practice worksheets on set and interval notation are a great way to strengthen knowledge and skills in this area. By providing answers to a set and interval notation worksheet, students can verify their solutions and gain confidence in their understanding of the topic. Additionally, reviewing the answers can help identify any areas of weakness or misconceptions that need to be addressed.
Overall, set and interval notation worksheet answers are a valuable resource for students and educators alike. They provide a way to assess understanding, practice applying the concepts, and reinforce learning in a clear and organized manner. By mastering set and interval notation, students can develop a strong foundation in algebra and confidently tackle more advanced mathematical concepts.
What is Set Notation?
Set notation is a way to represent and describe a set of numbers or objects. It uses mathematical symbols and notation to convey information about the elements in a set and how they are related to each other.
One of the main symbols used in set notation is the curly braces { }. Inside the braces, the elements of the set are listed. For example, the set of even numbers can be represented as {2, 4, 6, 8, …}.
- Union: The union of two sets is denoted by the symbol ∪ (cup). It represents all the elements that are present in either of the sets. For example, if A = {1, 2, 3} and B = {3, 4, 5}, then A ∪ B = {1, 2, 3, 4, 5}.
- Intersection: The intersection of two sets is denoted by the symbol ∩ (cap). It represents all the elements that are common to both sets. For example, if A = {1, 2, 3} and B = {3, 4, 5}, then A ∩ B = {3}.
- Complement: The complement of a set is denoted by the symbol ‘ (prime). It represents all the elements that are not in the given set. For example, if A = {1, 2, 3}, then A’ represents all the numbers that are not 1, 2, or 3.
Set notation also allows for the use of intervals to represent a range of numbers. Intervals can be open or closed, and they can be expressed using brackets or parentheses. For example, (1, 3) represents all the numbers between 1 and 3, excluding 1 and 3 themselves.
In conclusion, set notation is a powerful tool for representing and describing sets of numbers or objects. It enables us to convey information about the elements in a set, their relationships, and their range in a concise and precise manner.
How to Write Sets in Set Notation?
Set notation is a mathematical system used to describe collections or groups of objects or numbers. It allows us to express the elements of a set and the relationships between them in a concise and formal way. Being able to write sets in set notation is an essential skill in mathematics and is commonly used in various branches of the subject, including set theory, algebra, and calculus.
In set notation, a set is represented by enclosing its elements within curly braces {}. The elements of the set are listed inside the braces, separated by commas. For example, the set of even numbers less than 10 can be written as {2, 4, 6, 8}. This notation clearly defines the elements of the set and allows us to identify them easily.
Set-builder notation is another form of set notation that provides a more concise way to describe a set by specifying the properties or conditions that its elements must satisfy. It is often used when the set has an infinite number of elements or when it is difficult to list all the elements explicitly. In set-builder notation, the set is represented as {x | P(x)}, where x is the variable representing the elements of the set, and P(x) is a condition or property that x must satisfy.
For example, the set of all positive integers can be written as {x | x > 0}. This notation states that the set consists of all values of x that are greater than 0. Similarly, the set of all even numbers can be represented as {x | x is an even number}.
Interval notation is another way to express sets, particularly when dealing with sets of real numbers. In interval notation, a set is represented by using parentheses () and brackets [] to indicate whether the endpoints are included or excluded. For example, the interval (0, 5] represents the set of all real numbers greater than 0 and less than or equal to 5.
Overall, being able to write sets in set notation is crucial for effectively communicating mathematical concepts and relationships. Whether using curly braces, set-builder notation, or interval notation, these notations provide a clear and concise way to express sets and their properties.
What is Interval Notation?
In mathematics, interval notation is a way to express a set of numbers or points on a number line. It is commonly used to represent intervals, which are continuous ranges of values. Interval notation is a concise and clear way to convey information about these intervals, making it an essential tool in various mathematical fields.
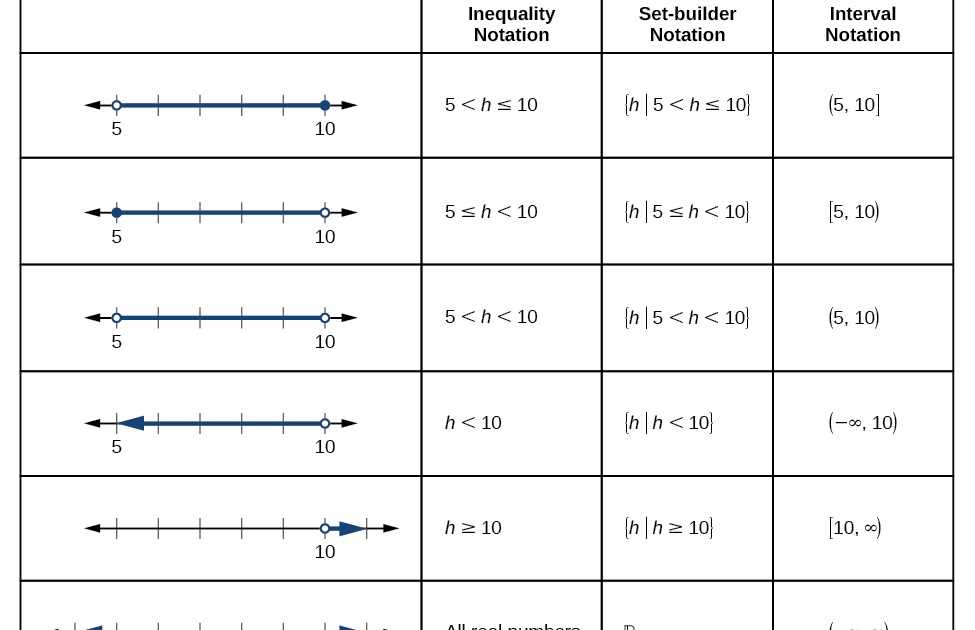
In interval notation, an interval is represented by a pair of numbers enclosed in brackets or parentheses, with the first number indicating the lower bound of the interval and the second number indicating the upper bound. The type of brackets or parentheses used depends on whether the endpoint is included or excluded from the interval. Square brackets [ ] denote inclusion, while round brackets ( ) denote exclusion.
For example, the interval notation [2, 7] represents the interval from 2 to 7, including both 2 and 7. On the other hand, the interval notation (5, 9) represents the interval from 5 to 9, excluding both 5 and 9. It is important to keep in mind that the numbers used as endpoints of the interval are themselves not part of the interval, unless specified otherwise.
Interval notation also allows for indicating infinite intervals. An infinite interval can be represented using the symbols -∞ (negative infinity) and ∞ (positive infinity). For instance, the interval notation (-∞, 4] represents all numbers less than or equal to 4, while the interval notation [3, ∞) represents all numbers greater than or equal to 3.
Using interval notation provides a compact and precise way to describe sets of numbers or points within a range. It is commonly used in various mathematical disciplines such as calculus, algebra, and statistics, where it enables concise communication and simplifies mathematical expressions.
How to Write Intervals in Interval Notation?
An interval is a set of real numbers that lies between two endpoints. Interval notation is a way to represent intervals using brackets and parentheses. It is a concise and organized way to express the range of numbers in a given interval.
There are four types of intervals that can be written in interval notation:
- Open interval: An open interval does not include the endpoints and is represented by using parentheses. For example, (1, 5) represents all real numbers between 1 and 5, excluding 1 and 5.
- Closed interval: A closed interval includes both endpoints and is represented by using brackets. For example, [2, 6] represents all real numbers between 2 and 6, including 2 and 6.
- Half-open interval: A half-open interval includes one endpoint and excludes the other. It is represented by using a combination of parentheses and brackets. For example, (3, 7] represents all real numbers between 3 and 7, excluding 3 but including 7.
- Unbounded interval: An unbounded interval extends indefinitely in one or both directions and is represented by using the symbols -∞ and/or +∞. For example, (-∞, 4) represents all real numbers less than 4, and (2, +∞) represents all real numbers greater than 2.
When writing intervals in interval notation, it is important to properly use the appropriate symbols and parentheses/brackets to accurately represent the range of numbers in the interval. Mastering interval notation can help simplify mathematical expressions and communicate mathematical ideas more effectively.
Set Notation vs Interval Notation: What’s the Difference?
In mathematics, there are different ways to represent sets of numbers, and two common notations are set notation and interval notation. While both notations serve the purpose of expressing a range of numbers, there are some key differences between them.
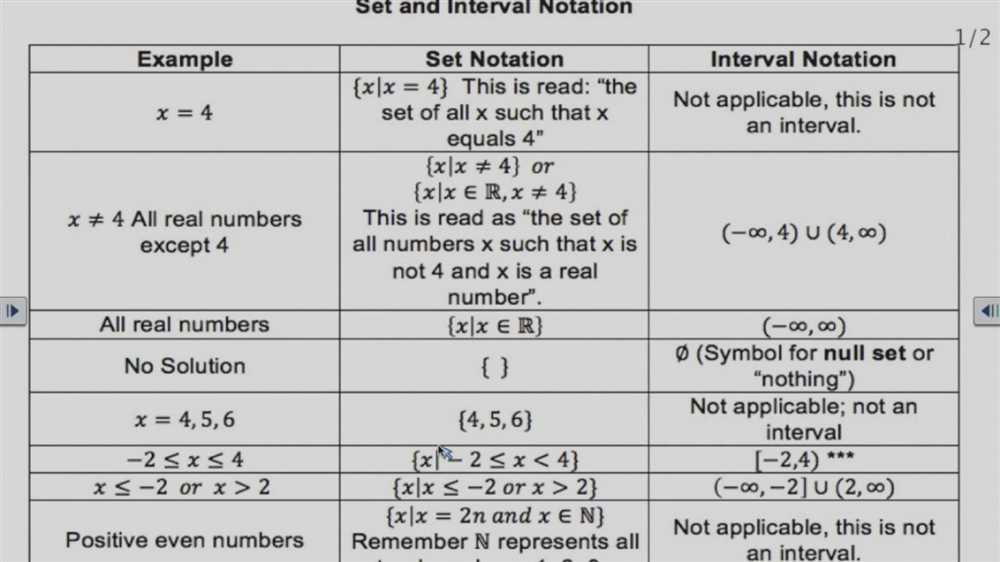
Set notation represents a collection of numbers enclosed within curly braces {}. For example, the set of natural numbers can be written as {1, 2, 3, …}. Set notation can also be used to represent specific conditions that the numbers must meet. For instance, the set of even numbers greater than 5 can be written as {x | x is an even number and x > 5}. Set notation allows for the inclusion of individual numbers as well as conditions.
Interval notation, on the other hand, represents a continuous range of numbers using intervals. An interval is represented by enclosing the starting and ending points within brackets or parentheses. The types of intervals include open intervals (excludes the endpoints), closed intervals (includes the endpoints), half-open intervals (one endpoint included and the other excluded), and half-closed intervals (one endpoint excluded and the other included).
To further illustrate the difference, let’s consider the set of real numbers between 0 and 1. In set notation, this can be written as {x | 0 < x < 1}. In interval notation, it can be represented as (0, 1) or [0, 1) or (0, 1]. The choice of brackets or parentheses indicates whether the endpoints are included or excluded.
- Set notation: {x | 0 < x < 1}
- Interval notation: (0, 1) or [0, 1) or (0, 1]
Both set notation and interval notation have their advantages and are used in different contexts. Set notation is more flexible and allows for the inclusion of specific conditions, while interval notation provides a more compact and concise representation of continuous ranges of numbers. Understanding the difference between the two notations is important for effectively communicating and understanding mathematical concepts.
Examples of Sets and Intervals in Set Notation

A set is a collection of distinct objects, called elements, which can be represented using set notation. Set notation uses brackets to enclose the elements of the set, and different types of brackets and symbols to indicate the relationship between elements.
1. Interval Notation: Interval notation is used to represent a range of numbers or values. There are four types of intervals: open intervals, closed intervals, half-open intervals, and half-closed intervals. An open interval does not include its endpoints, and is represented using parentheses. For example, (0, 1) represents all numbers between 0 and 1, excluding 0 and 1 themselves. A closed interval includes its endpoints, and is represented using brackets. For example, [0, 1] represents all numbers between 0 and 1, including 0 and 1. A half-open interval includes one endpoint but not the other, and is represented using a combination of brackets and parentheses. For example, [0, 1) represents all numbers between 0 and 1, including 0 but not 1. A half-closed interval includes one endpoint but not the other, and is represented using a combination of parentheses and brackets. For example, (0, 1] represents all numbers between 0 and 1, including 1 but not 0.
2. Set Builder Notation: Set builder notation is used to describe a set by specifying the properties or conditions that its elements must satisfy. It uses a vertical bar (|) or a colon (:) to separate the variable from its condition. For example, S = {x | x is a positive integer} represents the set of all positive integers.
3. Subset Notation: Subset notation is used to indicate that one set is a subset of another set. It uses the symbol ⊆ to represent subset. For example, A ⊆ B represents that set A is a subset of set B.
- Example: The set of natural numbers (N) is a subset of the set of integers (Z), so we can write N ⊆ Z.
4. Intersection and Union Notation: Intersection and union notation are used to combine sets. The intersection of two sets is the set of elements that are common to both sets, and is represented using the symbol ∩. The union of two sets is the set of elements that are in either of the two sets, and is represented using the symbol ∪.
- Example: Let A = {1, 2, 3} and B = {2, 3, 4}. The intersection of A and B is {2, 3}, represented as A ∩ B = {2, 3}. The union of A and B is {1, 2, 3, 4}, represented as A ∪ B = {1, 2, 3, 4}.
These are just a few examples of how sets and intervals can be represented using set notation. Set notation is a powerful tool for describing collections of objects and their relationships, and is widely used in mathematics and other fields.