In mathematics, representing linear nonproportional relationships is an essential concept that helps us understand the relationship between two variables that are not directly proportional. This skill is crucial in various fields, including economics, physics, and engineering. By learning how to represent these relationships, we can analyze data, make predictions, and solve real-world problems.
The answer key to the reteach activity on representing linear nonproportional relationships provides students with a guide to understand and practice this concept. It serves as a tool to reinforce the knowledge gained in class and to ensure that students can correctly represent these relationships on graphs and tables.
The answer key presents a series of exercises that require students to interpret given data, identify the relationship between the variables, and represent it graphically. It also includes step-by-step explanations of how to find the rate of change, the initial value, and the equation that represents the relationship. By following the answer key, students can gain a deeper understanding of the concept and develop their problem-solving skills.
Overall, the answer key for representing linear nonproportional relationships reteach provides a valuable resource for students to practice and master this essential skill. By using the key, students can improve their ability to interpret data, analyze relationships, and make predictions, which are all crucial skills in various academic and professional domains.
What is a linear nonproportional relationship?
A linear nonproportional relationship is a type of mathematical relationship between two variables where the rate of change is not constant. In a linear proportional relationship, the rate of change remains the same throughout, while in a linear nonproportional relationship, the rate of change can vary.
This type of relationship can be represented by a straight line on a graph, but the line will not pass through the origin. The slope of the line represents the rate of change between the two variables, and in a linear nonproportional relationship, this slope will change as you move along the graph.
When dealing with linear nonproportional relationships, it is important to analyze the slope of the line to determine the rate of change at different points. The equation of the line can be determined using the slope-intercept form, y = mx + b, where m is the slope and b is the y-intercept.
Examples of linear nonproportional relationships include the relationship between distance and time in nonuniform motion, where the speed of an object is not constant, and the relationship between temperature and altitude in the Earth’s atmosphere, where temperature changes nonproportionally with altitude.
In summary, a linear nonproportional relationship is a mathematical relationship between two variables where the rate of change is not constant. It can be represented by a straight line on a graph, but the line does not pass through the origin, and the slope of the line varies along the graph.
Definition and characteristics of linear nonproportional relationships
A linear nonproportional relationship is a mathematical relationship between two variables in which the rate of change is not constant. Unlike in a proportional relationship, where the variables change at a constant rate, in a linear nonproportional relationship, the rate of change can vary.
This type of relationship can be represented graphically by a line on a coordinate plane. The line may have a positive or negative slope, indicating whether the variables increase or decrease together. However, the line will not intersect or pass through the origin, as it would in a proportional relationship.
The characteristics of a linear nonproportional relationship can also be described algebraically. The relationship can be represented by a linear equation in the form y = mx + b, where y represents the dependent variable, x represents the independent variable, m represents the slope of the line, and b represents the y-intercept. The slope of the line indicates the rate at which the dependent variable changes with respect to the independent variable.
One key characteristic of a linear nonproportional relationship is that the ratio of y to x is not constant. As x increases or decreases, the corresponding values of y will change, but not at a constant rate. Additionally, the y-intercept, b, represents the value of y when x is equal to zero. It indicates the initial value of y before any changes in x.
Understanding and recognizing linear nonproportional relationships is essential in various fields such as economics, physics, and engineering. By analyzing these relationships, researchers and professionals can make informed decisions and predictions based on the behavior of the variables involved.
Understanding the representation of linear nonproportional relationships is an important concept in mathematics. A linear relationship is one in which the rate of change is constant. This means that as one variable increases, the other variable increases at a constant rate. In a nonproportional relationship, the rate of change is not constant, meaning that as one variable increases, the other variable does not increase at the same rate.
When representing linear nonproportional relationships, it is important to understand the different representations that can be used. One common representation is a graph, where the independent variable is plotted on the x-axis and the dependent variable is plotted on the y-axis. The points on the graph will form a straight line, indicating that there is a linear relationship between the variables.
Another representation is a table, where the values of the independent variable are listed in one column and the corresponding values of the dependent variable are listed in another column. The relationship between the variables can be observed by looking for patterns in the values.
In addition to graphs and tables, equations can also be used to represent linear nonproportional relationships. The equation y = mx + b represents a linear relationship, where m is the slope of the line and b is the y-intercept. The slope represents the rate of change, while the y-intercept represents the starting point of the line.
Understanding how to represent linear nonproportional relationships is essential for solving real-world problems and analyzing data. By using graphs, tables, and equations, mathematicians can better understand the relationship between variables and make predictions or draw conclusions.
Graphical representation of linear nonproportional relationships

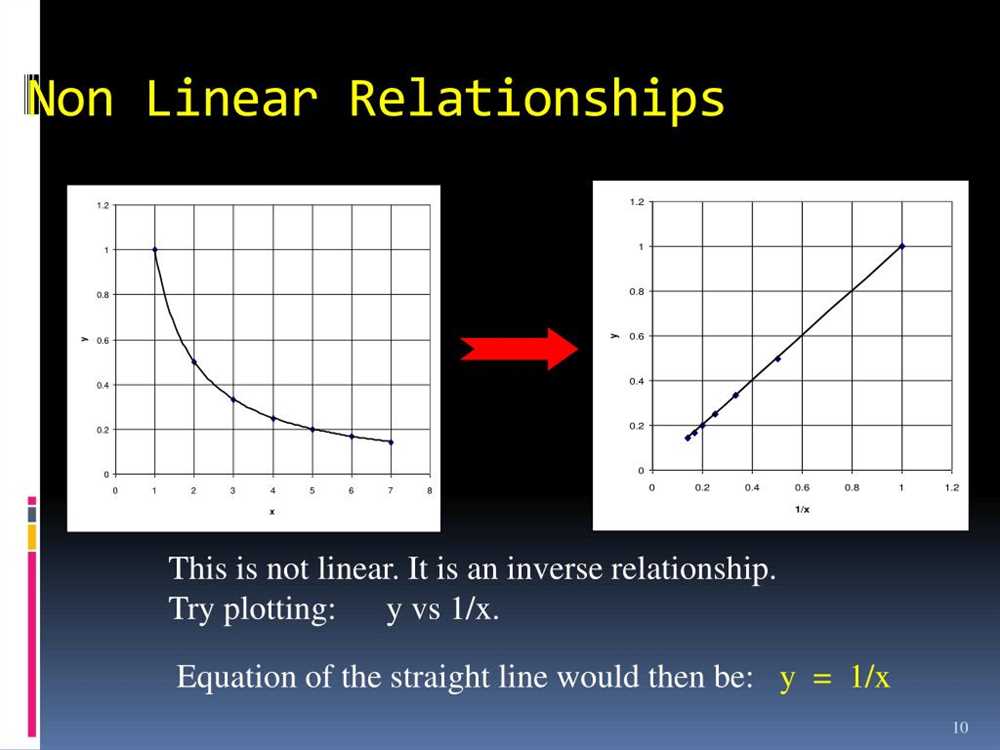
The graphical representation of linear nonproportional relationships allows us to visualize the relationship between two variables and identify patterns or trends. In this context, a linear nonproportional relationship refers to a situation where the ratio between the two variables is not constant, but still follows a linear pattern. It means that as one variable increases, the other variable also increases, but not at a constant rate.
One way to represent a linear nonproportional relationship graphically is by creating a scatter plot. A scatter plot is a graph that uses dots to represent individual data points. Each dot on the graph corresponds to a pair of values for the two variables being compared. The x-axis represents one variable, and the y-axis represents the other variable. By plotting each pair of values on the scatter plot, we can see the overall pattern or trend of the relationship.
When analyzing a scatter plot for a linear nonproportional relationship, we look for the general direction of the dots. If the dots cluster around a straight line, it suggests a linear relationship. However, if the dots do not follow a straight line, it indicates a nonproportional relationship. In this case, we may need to use other mathematical methods, such as calculating a line of best fit, to determine the equation that represents the relationship between the variables.
To understand the relationship between variables better, we can also calculate and interpret the slope and y-intercept of the line of best fit. The slope represents the rate of change between the variables, while the y-intercept represents the starting point of the relationship. By analyzing the slope and y-intercept, we can make predictions and draw conclusions about the relationship between the variables.
Overall, the graphical representation of linear nonproportional relationships is a powerful tool for analyzing data and understanding the relationship between variables. By creating scatter plots and calculating the line of best fit, we can visualize the pattern or trend and make informed conclusions based on the data.
Solving linear nonproportional equations
When solving linear nonproportional equations, it is important to remember that the relationship between the variables is not always directly proportional. This means that the rate of change is not constant, and the graph of the equation will not be a straight line.
To solve these types of equations, you can use a variety of methods, including substitution, elimination, and graphing. The goal is to find the values of the variables that make the equation true.
Substitution
- In substitution, you solve one equation for one variable and substitute that expression into the other equation.
- By replacing one variable with the expression in terms of the other variable, you can solve for the remaining variable.
- Substitution allows you to eliminate one variable and solve for the other.
Elimination
- In elimination, you manipulate both equations so that the coefficients of one variable are additive inverses.
- By adding or subtracting the equations, you can eliminate one variable and solve for the remaining variable.
- Elimination allows you to find the values of the variables that make the system of equations true.
Graphing
- When graphing linear nonproportional equations, the resulting graph will not be a straight line.
- You can plot the points and draw a curve that best fits the data.
- Graphing can help you visually understand the relationship between the variables and find the solution to the equation.
Overall, solving linear nonproportional equations requires careful manipulation of the equations to eliminate variables and find the values that make the equations true. Whether using substitution, elimination, or graphing, the goal is to determine the solution to the equation and understand the relationship between the variables.
Methods and Strategies for Solving Linear Nonproportional Equations
Solving linear nonproportional equations requires a systematic approach and the use of various methods and strategies. One of the most common techniques is the substitution method, where one equation is solved for one variable and that expression is substituted into the other equation. This allows us to solve for the remaining variable.
Another method is the elimination method, where both equations are manipulated to eliminate one variable when they are added or subtracted together. This results in a new equation with only one variable, which can be easily solved. The elimination method is particularly useful when the coefficients of one of the variables are the same in both equations.
In some cases, graphing the equations can help visualize the solution to a linear nonproportional equation. The graphs of the two equations will intersect at the point where the solutions to both equations coincide. This point represents the values of the variables that satisfy both equations simultaneously.
When dealing with more complex systems of linear nonproportional equations, it may be necessary to use matrix methods or software programs that can handle these calculations efficiently. These tools allow for the simultaneous solution of multiple equations, saving time and reducing errors.
Overall, there are various methods and strategies available for solving linear nonproportional equations, and the choice of approach depends on the specific problem at hand. By understanding and applying these techniques effectively, it is possible to find solutions to these types of equations accurately and efficiently.
Representing linear nonproportional relationships using tables
Tables are a useful tool for representing linear nonproportional relationships. They allow us to organize and display data in an organized manner, making it easier to identify patterns and relationships between variables. In the context of linear nonproportional relationships, tables can be used to show how one variable changes in relation to another.
When representing linear nonproportional relationships using tables, it is important to include columns for both variables involved in the relationship. The first column should represent the values of the independent variable, while the second column should represent the corresponding values of the dependent variable. By listing the values of both variables side by side, we can easily see how they are related and identify any patterns or trends.
For example, if we are studying the relationship between the number of hours studied and the corresponding test scores, we can create a table with the hours studied in the first column and the test scores in the second column. By filling in the table with the appropriate values, we can visually see how the test scores change as the number of hours studied increase or decrease.
Using tables to represent linear nonproportional relationships can make it easier to analyze data and draw conclusions. It allows us to visualize the relationship between variables and identify any outliers or anomalies. Additionally, tables make it easier to compare multiple sets of data and make predictions based on the observed patterns. Overall, tables are a valuable tool in representing and analyzing linear nonproportional relationships.
Creating and interpreting tables for linear nonproportional relationships
Creating and interpreting tables is an important skill in understanding linear nonproportional relationships. Tables provide a visual representation of data and can help us identify patterns and trends. In the context of linear nonproportional relationships, tables can help us determine if there is a constant rate of change between two variables or if the relationship is nonlinear.
To create a table for a linear nonproportional relationship, we first need to identify the two variables involved. Let’s take the example of comparing the number of hours spent studying for an exam to the corresponding test scores. We can create a table with two columns: one for the number of hours and another for the test scores.
We can then populate the table by choosing specific values for the number of hours and calculating the corresponding test scores. For example, we can choose the numbers 1, 2, 3, and so on for the number of hours, and calculate the test scores based on a predetermined equation or real-world data. By inputting these values into the table, we can observe any patterns or relationships between the two variables.
To interpret the table, we can look for patterns in the data. If there is a constant rate of change between the number of hours and the test scores, we will see that the test scores increase or decrease by the same amount for each additional hour of study. If there is a nonlinear relationship, the test scores may not follow a consistent pattern.
In summary, creating and interpreting tables is a useful tool in understanding linear nonproportional relationships. Tables allow us to visualize and analyze data, identify patterns, and determine if there is a constant rate of change between two variables or a nonlinear relationship.