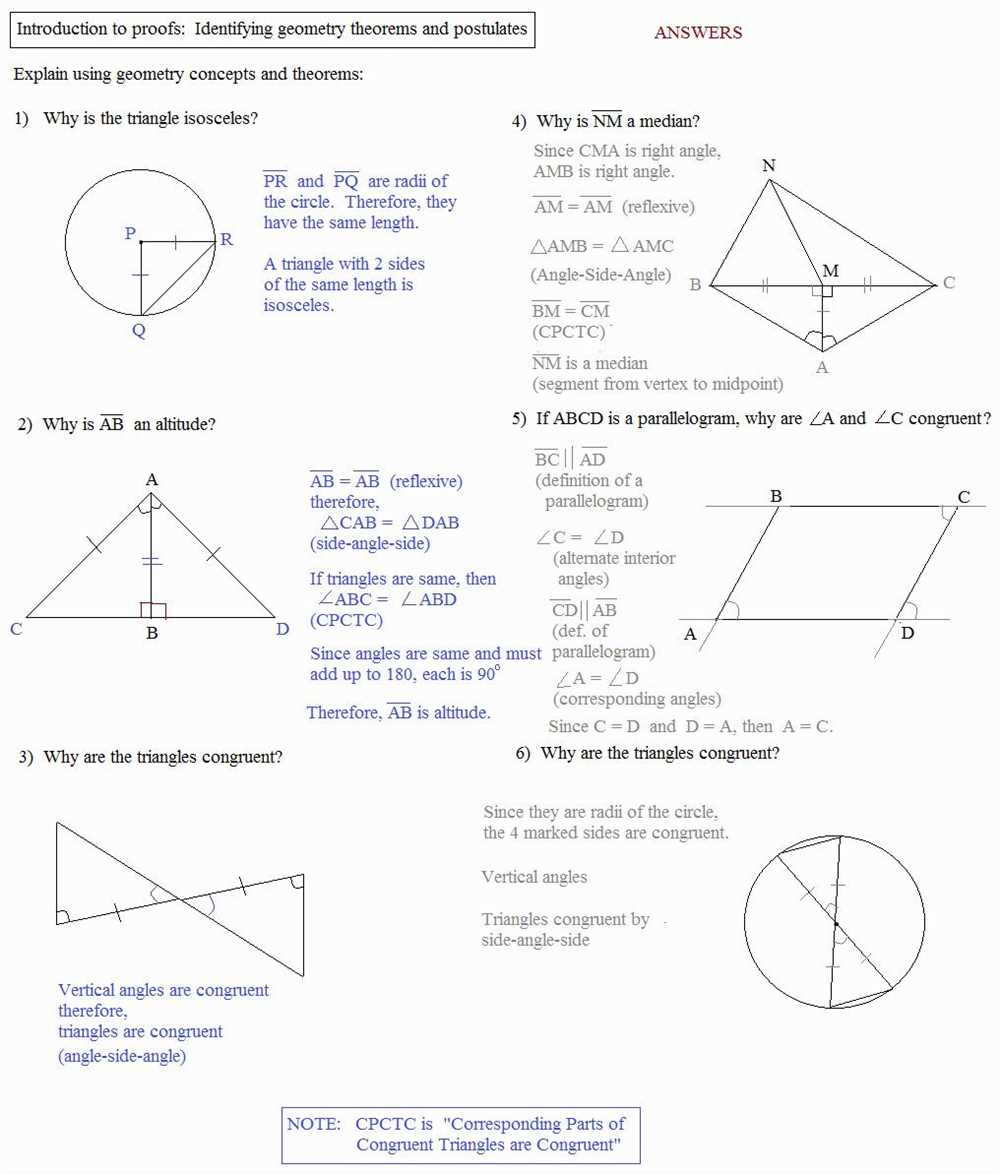
In the world of geometry, Cpctc stands for Corresponding Parts of Congruent Triangles are Congruent. This simple yet powerful theorem is often used to solve various geometric problems and prove the congruence of different parts of triangles. To better understand Cpctc and its applications, let’s take a look at a worksheet and its corresponding answers.
Geometry worksheets often present students with a set of triangles and various angles, sides, or segments within them. The goal is to analyze the given information and apply different theorems and postulates to solve for missing measures or prove congruence. Cpctc plays a crucial role in these worksheets as it allows for the identification of congruent angles, sides, or segments based on the congruence of the triangles themselves.
By examining the solutions to a Cpctc worksheet, students can learn how to use the theorem effectively in their own problem-solving. They will discover that proving the congruence of triangles is a key step in solving for missing measures or proving congruence of corresponding parts, such as angles or sides. The answers to the Cpctc worksheet provide a clear demonstration of how the theorem can be applied and how it helps in the overall understanding of geometric concepts.
Overall, Cpctc is a fundamental tool in geometry that enables students to solve geometric problems with precision and confidence. By studying the answers to a Cpctc worksheet, students can enhance their knowledge of congruence and proofs, and develop their analytical thinking skills. Understanding Cpctc opens the door to further exploration of geometric theorems and postulates, and empowers students to tackle more complex geometric problems.
Cpctc Worksheet Answers

Welcome to our Cpctc worksheet answers! In geometry, Cpctc stands for “Corresponding Parts of Congruent Triangles are Congruent.” This concept is used to prove that two triangles are congruent by showing that their corresponding parts, such as sides and angles, are congruent.
In our worksheet, you will find a series of triangle pairs for which you need to determine if they are congruent. Each pair will have specific information given, such as side lengths or angle measures. You will then use the Cpctc principle to identify the congruent parts and justify your answer.
Let’s take a look at an example question from the worksheet:
Example:
Triangle ABC is congruent to triangle DEF. Given that angle A = angle D and side AB = side DE, prove that angle B = angle E.
In this example, we are given two congruent triangles, ABC and DEF. We know that angle A is congruent to angle D and side AB is congruent to side DE. Using the Cpctc principle, we can conclude that angle B must be congruent to angle E. This is because corresponding angles of congruent triangles are equal.
You will encounter similar questions in our Cpctc worksheet. Remember to carefully analyze the given information and use the Cpctc principle to determine congruence. Practice makes perfect, so take your time and enjoy solving the problems! Good luck!
Understanding Cpctc: What It Means and How It’s Used
CPCTC stands for “Corresponding Parts of Congruent Triangles are Congruent.” It is a fundamental concept in geometry that helps prove the congruence of two or more triangles. In simple terms, Cpctc states that if two triangles are congruent, then their corresponding parts (angles or sides) are also congruent.
Cpctc is based on the fact that congruent triangles have the same shape and size. When two triangles are proven to be congruent using methods like SSS (Side-Side-Side), SAS (Side-Angle-Side), ASA (Angle-Side-Angle), or AAS (Angle-Angle-Side), the concept of Cpctc is used to establish the congruence of their corresponding parts.
For example, suppose we have two triangles, triangle ABC and triangle DEF. If we can prove that triangle ABC is congruent to triangle DEF using one of the mentioned congruence methods, then we can apply Cpctc to conclude that angle A is congruent to angle D, side AB is congruent to side DE, angle B is congruent to angle E, and so on.
In summary, Cpctc helps us build arguments in geometry by extending the congruence of triangles to their corresponding angles or sides. It allows us to make further conclusions about the relationships between various parts of congruent triangles, which is essential in solving geometric problems and creating proofs.
Key Concepts: Corresponding Parts of Congruent Triangles
In geometry, congruent triangles are triangles that have the same shape and size. When two triangles are congruent, their corresponding parts (sides and angles) are also congruent. This means that the corresponding angles of congruent triangles are equal, and the corresponding sides are of equal length.
One key concept related to congruent triangles is the Corresponding Parts of Congruent Triangles (CPCTC) theorem. CPCTC states that if two triangles are congruent, then their corresponding parts are also congruent. This theorem allows us to prove various properties and relationships between triangles based on their congruence.
To use CPCTC, we first need to determine if two triangles are congruent. There are several methods to prove congruence, such as the Side-Side-Side (SSS) criterion, the Side-Angle-Side (SAS) criterion, and the Angle-Side-Angle (ASA) criterion. Once we have established congruence, we can apply CPCTC to prove other properties of the congruent triangles.
For example, if we have two congruent triangles ABC and DEF, we can use CPCTC to prove that their corresponding angles are equal. This is done by stating that angle A is congruent to angle D, angle B is congruent to angle E, and angle C is congruent to angle F. Similarly, we can use CPCTC to prove that the corresponding sides of these triangles are of equal length.
In conclusion, understanding the concept of corresponding parts of congruent triangles is crucial in geometry. It allows us to make conclusions about the angles and sides of congruent triangles based on their congruence. By applying the CPCTC theorem, we can prove various properties and relationships between congruent triangles.
Applying Cpctc in Triangle Congruence Proofs
In geometry, Cpctc stands for “Corresponding Parts of Congruent Triangles are Congruent”. It is a powerful tool used to prove triangle congruence in various geometric proofs. Cpctc states that if two triangles are congruent, then their corresponding parts, such as angles and sides, are also congruent.
When applying Cpctc in triangle congruence proofs, it is essential to identify the congruent triangles first. This can be done by using the congruence postulates, such as Side-Side-Side (SSS), Side-Angle-Side (SAS), Angle-Side-Angle (ASA), or Angle-Angle-Side (AAS). Once the congruent triangles are identified, Cpctc can be used to prove the congruence of specific parts of the triangles.
For example, suppose we are given two triangles, triangle ABC and triangle DEF, and we want to prove that they are congruent. We can show that angle A is congruent to angle D, side AB is congruent to side DE, and angle B is congruent to angle E. By applying Cpctc, we can then conclude that angle C is congruent to angle F and side BC is congruent to side EF.
In triangle congruence proofs, Cpctc is a powerful tool that allows us to make conclusions about the congruent parts of triangles. It simplifies the process of proving triangle congruence by leveraging the fact that corresponding parts of congruent triangles are congruent. By utilizing Cpctc effectively, we can confidently establish the congruence of triangles in geometric proofs.
Proving Triangle Congruence Using CPCTC
In geometry, CPCTC stands for “Corresponding Parts of Congruent Triangles are Congruent”. It is a valuable theorem that allows us to prove triangle congruence by showing that corresponding parts of two triangles are congruent. This theorem is essential in geometry proofs and helps establish the equality of angles and sides within triangles.
When proving triangle congruence using CPCTC, we follow a step-by-step process. First, we identify the given information and the triangles involved. We then look for congruent pairs of corresponding parts, such as angles or sides, within the triangles. These corresponding parts should be congruent based on the given information.
Next, we state the congruence of the triangles by listing their corresponding parts. For example, if angle A is congruent to angle D and side AB is congruent to side DE, we can state that triangle ABC is congruent to triangle DEF using the CPCTC theorem.
Finally, we conclude the proof by stating that all other corresponding parts of the triangles are congruent. This means that if angle A is congruent to angle D and side AB is congruent to side DE, then all corresponding angles and sides of the triangles will also be congruent.
- CPCTC is a powerful tool in geometry proofs that allows us to establish triangle congruence.
- It helps us prove that triangles are congruent by showing that their corresponding parts are congruent.
- The process involves identifying the given information, finding congruent corresponding parts, stating the congruence of the triangles, and concluding the proof by stating that all other corresponding parts are congruent.
- CPCTC is widely used in geometry to solve problems and prove theorems related to triangles and their properties.
Examples of CPCTC Worksheet Problems
CPCTC, or Corresponding Parts of Congruent Triangles are Congruent, is a theorem in geometry that allows us to make conclusions about congruent triangles and their corresponding parts. This theorem is often used in problem-solving exercises to prove the congruence of triangle parts based on congruence of the triangles themselves. Let’s look at some examples of CPCTC worksheet problems to better understand how this theorem is applied.
Example 1: Given two congruent triangles, Triangle ABC and Triangle DEF, with corresponding sides AB and DE, angles B and E, and angle C and angle F, we are asked to prove that corresponding angles A and D are congruent. To solve this problem, we can use the CPCTC theorem. Since Triangle ABC and Triangle DEF are congruent, we know that all corresponding parts are congruent. Thus, we can conclude that angles A and D are congruent based on CPCTC.
Example 2: In this problem, we are given two congruent triangles, Triangle PQR and Triangle XYZ, with corresponding sides PQ and XY, QR and YZ, and angles P and X. The problem asks us to prove that angle R is congruent to angle Z. Using CPCTC, we can state that since the triangles are congruent, angles R and Z are corresponding angles and must be congruent.
Overall, CPCTC allows us to make conclusions about the congruence of triangle parts based on the congruence of the triangles themselves. By understanding and applying this theorem, we can confidently solve various geometry problems and prove congruence between corresponding parts of congruent triangles.
Exploring Different Scenarios: Cpctc Practice
In the field of geometry, Cpctc (Corresponding Parts of Congruent Triangles are Congruent) is an important concept that helps to prove triangle congruence. By understanding the different scenarios in which Cpctc can be applied, we can enhance our problem-solving skills and deepen our understanding of triangle congruence.
One scenario where Cpctc can be applied is when we have two congruent triangles and we need to prove that certain corresponding parts are congruent. For example, if we are given two congruent triangles ABC and DEF, and we know that AB is congruent to DE and angle A is congruent to angle D, we can conclude that angle B is congruent to angle E using Cpctc.
In another scenario, Cpctc can be used to prove the congruence of two triangles based on the congruence of their corresponding parts. If we are given that angle A is congruent to angle D, angle B is congruent to angle E, and side AB is congruent to side DE, we can use Cpctc to prove that triangle ABC is congruent to triangle DEF.
By practicing Cpctc problems, we can develop our logical thinking and reasoning skills. It allows us to apply the properties of congruent triangles to prove various statements and solve complex geometric puzzles. With each practice, we become more proficient in using Cpctc effectively and efficiently in our geometry proofs.
Tips and Tricks for Solving Cpctc Worksheet Problems
When it comes to solving Cpctc worksheet problems, it is important to have a clear understanding of the Cpctc theorem and its applications. Cpctc stands for “Corresponding Parts of Congruent Triangles are Congruent,” and it is a critical concept in geometry. Here are some tips and tricks to help you successfully solve Cpctc worksheet problems:
- Start by identifying congruent triangles: Look for triangles in the given diagram that have congruent corresponding parts. These can be sides or angles that are marked as congruent or can be inferred from other information given.
- Label the corresponding parts: Once you have identified congruent triangles, label the corresponding parts. This will help you keep track of which parts are congruent and which are not.
- Use Cpctc to draw conclusions: Cpctc allows you to make conclusions about other parts of the congruent triangles. If two triangles have congruent corresponding angles, for example, you can conclude that their remaining angles are congruent as well.
- Pay attention to congruent sides and angles: When using Cpctc, make sure to consider both the sides and angles that are congruent. Look for opportunities to apply the theorem to all the congruent parts.
- Apply known properties and theorems: In addition to Cpctc, use other known properties and theorems to solve the problems. These can include the Pythagorean theorem, the angle sum property of triangles, and the properties of parallel lines.
By following these tips and tricks, you will be able to approach Cpctc worksheet problems with confidence and effectively apply the Cpctc theorem to find the missing information. Remember to carefully analyze the given information, label the congruent parts, and draw logical conclusions based on Cpctc and other relevant geometric concepts.
Common Mistakes to Avoid in Cpctc Worksheet Answers

When it comes to completing Cpctc worksheet answers, there are some common mistakes that students often make. These mistakes can lead to incorrect solutions and a misunderstanding of the Cpctc concept. It is important to be aware of these mistakes and take steps to avoid them in order to achieve accurate and successful answers.
1. Skipping Steps: One common mistake is skipping steps in the given proof. Cpctc stands for “corresponding parts of congruent triangles are congruent.” It is essential to carefully analyze and understand each step provided in the proof and apply them correctly in order to arrive at the correct answer. Skipping steps can lead to confusion and incorrect conclusions.
2. Not Properly Identifying Corresponding Parts: Another common mistake is not properly identifying the corresponding parts of congruent triangles. It is important to clearly identify which parts of the triangles are congruent and how they correspond to each other. This includes sides, angles, and any other relevant elements. Failing to do so can result in incorrect answers and a misunderstanding of Cpctc.
3. Misapplying the Cpctc Concept: An additional mistake is misapplying the Cpctc concept. It is crucial to understand the conditions necessary for applying Cpctc and to only apply it when those conditions are met. Using Cpctc in situations where it does not apply can lead to incorrect answers and a misunderstanding of the concept.
4. Lack of Clarity in Explanation: Lastly, a common mistake is a lack of clarity in the explanation of Cpctc worksheet answers. It is important to clearly communicate the thought process and reasoning behind each step and answer. This helps others, such as teachers or classmates, understand the solution and provides an opportunity for feedback and clarification.
By being aware of these common mistakes and actively avoiding them, students can improve their understanding of Cpctc and achieve accurate and successful worksheet answers.