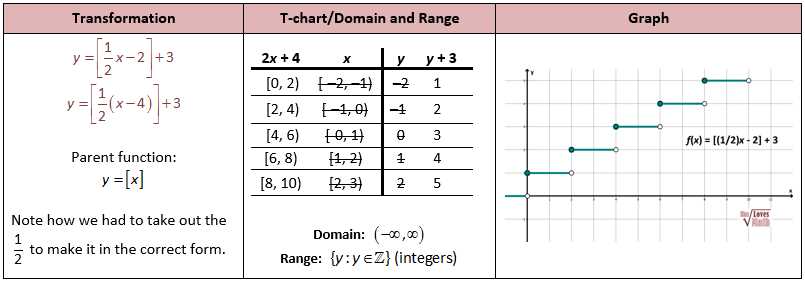
Understanding how to work with linear functions and their transformations is crucial for mastering algebra and graphing skills. In this article, we will explore the topic of transformations of linear functions and provide answers to practice problems in the “3 7 practice transformations of linear functions” form K.
Linear functions can be transformed in various ways, including translations, reflections, stretches, and compressions. These transformations alter the shape, position, and orientation of the graph of a linear function in the coordinate plane. By learning the rules and properties associated with these transformations, students can manipulate linear functions to accurately represent different situations and analyze their behavior.
The “3 7 practice transformations of linear functions” form K provides a set of practice problems that allow students to apply their understanding of transformations to specific linear functions. By identifying the type of transformation (translation, reflection, stretch, or compression), determining the direction and magnitude of the transformation, and correctly graphing the transformed function, students can strengthen their skills in visualizing and working with linear functions. The answers provided in this article will serve as a helpful resource for students to check their work and reinforce their understanding of transformations.
Understanding Linear Functions
Linear functions are a fundamental concept in mathematics that play a crucial role in various fields such as physics, economics, and engineering. They represent a linear relationship between two variables, where the rate of change is constant. These functions are characterized by a straight line when graphed on a cartesian coordinate system.
A linear function can be expressed in the form y = mx + b, where m represents the slope of the line and b represents the y-intercept. The slope indicates the rate at which the line rises or falls, while the y-intercept represents the point where the line crosses the y-axis.
Graphical representation. When graphing a linear function, it is essential to plot at least two points on the line to determine its direction and steepness. These points can be found by assigning values to x and solving for y using the equation of the line. Alternatively, the slope-intercept form allows us to identify the y-intercept and use the slope to find additional points.
Transformations. Linear functions can also undergo transformations that change their appearance on a graph. These transformations include translations, reflections, dilations, and vertical or horizontal stretches or compressions. Each transformation affects the slope and intercept of the function differently, leading to a change in the overall shape of the line.
In conclusion, understanding linear functions is crucial in various fields and is fundamental in mathematics. By grasping the concepts of slope, y-intercept, graphical representation, and transformations, one can analyze and interpret linear relationships and use them to solve real-life problems.
What are Linear Functions?
A linear function is a mathematical model that represents a relationship between two variables in a straight line. It is one of the most basic and commonly used types of functions in mathematics. Linear functions are often used to describe real-world situations and analyze data.
In a linear function, the rate of change between the two variables remains constant. This means that for every unit increase or decrease in one variable, there is a consistent corresponding increase or decrease in the other variable. The equation of a linear function can be written as y = mx + b, where m represents the slope of the line and b represents the y-intercept.
The slope of a linear function determines the steepness of the line. A positive slope indicates an upward line, while a negative slope indicates a downward line. The y-intercept represents the point where the line crosses the y-axis. By analyzing the slope and y-intercept, we can determine various characteristics of the linear function, such as its direction, starting point, and rate of change.
Linear functions are useful in many areas, including economics, physics, engineering, and finance. They can be used to analyze data trends, make predictions, and solve real-world problems. Understanding linear functions is essential for building a solid foundation in mathematics and developing problem-solving skills.
Properties of Linear Functions
A linear function is a mathematical function that can be represented by a straight line on a coordinate plane. Understanding the properties of linear functions is essential for analyzing and solving problems involving lines. These properties help us describe and interpret the behavior of linear functions.
1. Slope:

The slope of a linear function represents the steepness of the line. It is the ratio of the change in y-coordinates to the change in x-coordinates between two points on the line. A positive slope indicates an upward line, while a negative slope indicates a downward line. A slope of zero represents a horizontal line, and an undefined slope represents a vertical line.
2. Y-intercept:
The y-intercept of a linear function is the point where the line crosses or intersects the y-axis. It is the value of y when x is equal to zero. The y-intercept can be identified by looking at the equation of the line in the form y = mx + b, where b is the y-intercept.
3. Linearity:
Linear functions have a constant rate of change, meaning that the slope remains the same throughout the line. This property allows us to predict the behavior of the function for different values of x. If the slope is positive, the function increases as x increases. If the slope is negative, the function decreases as x increases.
4. Shifts:
Linear functions can be shifted or translated horizontally or vertically. A horizontal shift occurs when the x-value of every point on the line is increased or decreased by a constant value. This affects the position of the line on the x-axis. A vertical shift occurs when the y-value of every point on the line is increased or decreased by a constant value. This affects the position of the line on the y-axis.
By understanding these properties, we can analyze and solve problems involving linear functions, such as finding the equation of a line, determining the slope and y-intercept, identifying parallel or perpendicular lines, and predicting the behavior of a function for different inputs.
Transformations of Linear Functions
Linear functions are mathematical representations of relationships that exhibit a constant rate of change. The graph of a linear function is a straight line, and it can be transformed by various operations such as translations, reflections, stretches, and compressions. These transformations can change the position, shape, and size of the linear function.
One common transformation of a linear function is a translation, which involves shifting the entire graph horizontally or vertically. If we add a constant value to the function, the graph will shift upwards, and if we subtract a constant value, the graph will shift downwards. Similarly, adding or subtracting a constant value from the input variable will shift the graph horizontally.
Another transformation of a linear function is a reflection, which involves flipping the graph over a line. A reflection over the x-axis will change the sign of the function’s output values, while a reflection over the y-axis will change the sign of the function’s input values. These reflections can result in the graph being upside down or facing in the opposite direction.
Stretching or compressing a linear function involves changing the slope of the graph. If we multiply the function by a constant greater than 1, it will be stretched vertically, making it steeper. On the other hand, multiplying the function by a constant between 0 and 1 will compress it vertically, making it less steep. These transformations affect the rate of change of the function.
Overall, transformations of linear functions can alter their position, shape, and size. By performing these transformations, we can manipulate the behavior of the function and explore its different characteristics.
What are Transformations?
Transformations in mathematics refer to the changes or manipulations made to a mathematical object, such as a line or a function. These transformations can be applied to different types of objects, but in this context, we will focus on transformations of linear functions.
Transformations of linear functions involve changing their position, size, or orientation on a coordinate plane. They can be classified into four main categories: translations, reflections, dilations, and rotations.
Translations:
A translation is a transformation that slides a linear function in a specific direction without changing its orientation or size. It involves shifting the entire function horizontally or vertically on a coordinate plane. Translations can be described using vector notation or by indicating the amount of shift in units.
Reflections:
A reflection is a transformation that flips a linear function over a line, called the line of reflection. This line acts as a mirror, and the function is symmetrical with respect to it. Reflections can be vertical, horizontal, or diagonal, depending on the line of reflection.
Dilations:
A dilation is a transformation that changes the size of a linear function while preserving its shape and orientation. It involves stretching or compressing the function either horizontally or vertically. Dilations can be described by a scale factor, which indicates the amount of stretching or compressing.
Rotations:
A rotation is a transformation that turns a linear function around a fixed point called the center of rotation. The function is rotated by a certain angle, either clockwise or counterclockwise. Rotations can be described by the angle of rotation and the center of rotation.
Understanding and applying transformations of linear functions is important in various areas of mathematics, such as geometry and calculus. They allow us to manipulate functions to better understand their properties and relationships.
Types of Transformations
Linear functions can be transformed in different ways to create new functions with specific characteristics. These transformations can change the position, size, and shape of the original function. There are four main types of transformations that can be applied to linear functions: translation, reflection, dilation, and rotation.
1. Translation:
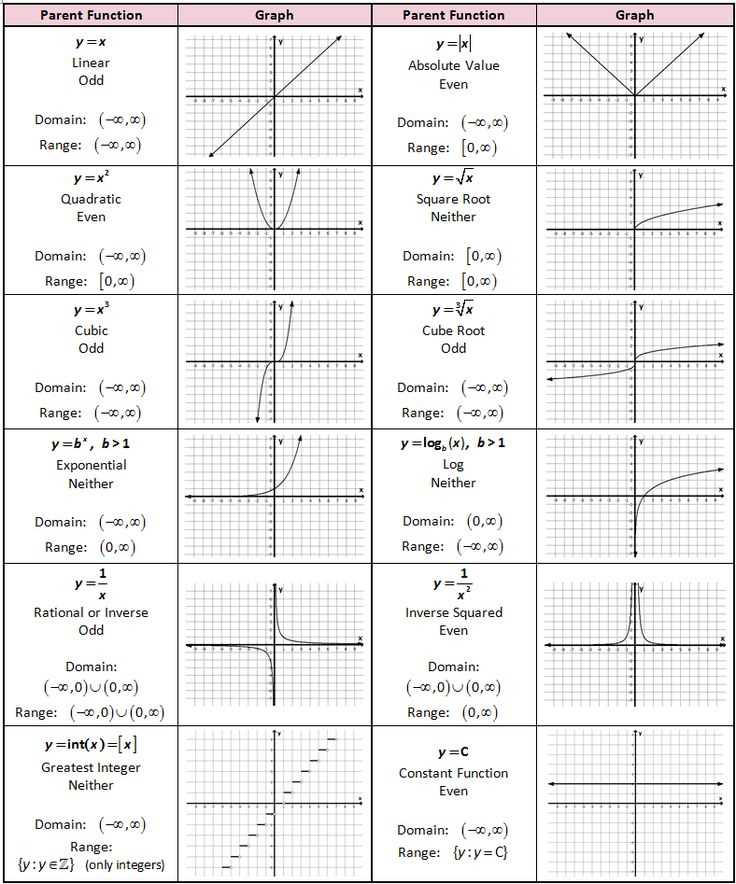
A translation involves shifting the entire function horizontally or vertically without changing its shape. The function is moved by adding or subtracting a constant value to the x or y coordinates. For example, if we add 2 to the x-coordinate of every point on the function, the graph will be shifted 2 units to the right. Similarly, adding or subtracting a constant value from the y-coordinate will shift the graph up or down.
2. Reflection:
Reflection involves flipping the function across a line, known as the line of reflection. This line can be the x-axis, the y-axis, or any other line in the coordinate plane. To reflect a function across the x-axis, we multiply the y-coordinate of every point by -1. Similarly, reflecting across the y-axis involves multiplying the x-coordinate by -1. Reflecting across other lines requires more advanced transformations, such as using the equations of the lines.
3. Dilation:
Dilation involves stretching or shrinking the function while keeping its shape. This transformation is performed by multiplying the x-coordinate or the y-coordinate of every point by a constant value greater than 1 (for stretching) or between 0 and 1 (for shrinking). The choice of the constant determines the degree of dilation. A constant greater than 1 results in an expansion, while a constant between 0 and 1 leads to a compression.
4. Rotation:
Rotation involves turning the function around a fixed point on the coordinate plane. The angle and direction of rotation determine the new position of each point. This transformation can be achieved using rotation matrices or formulas, which rotate the x and y coordinates of the points. The rotation can be clockwise or counterclockwise, depending on the angle of rotation.
These types of transformations allow us to manipulate linear functions and create a variety of new functions with different characteristics. By understanding and applying these transformations, we can analyze and graph linear functions in different ways to explore their properties and relationships.
Seven Practice Transformations
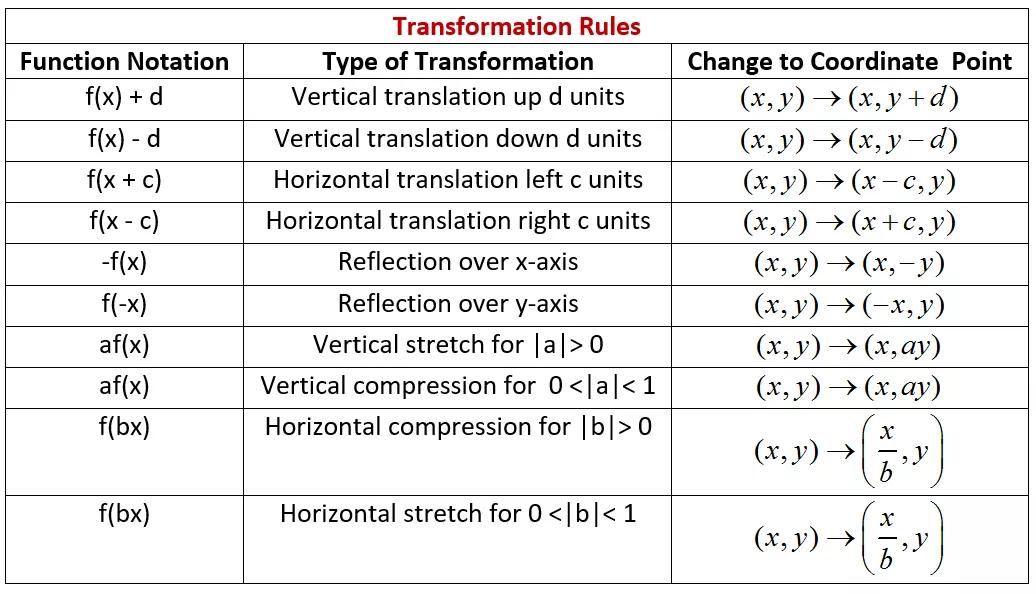
Transformations of linear functions are an important concept in mathematics. By applying different transformations to a linear function, we can change its shape, position, and direction. Understanding these transformations can help us analyze and solve various mathematical problems.
There are seven main types of transformations that can be applied to linear functions: translation, reflection, dilation, rotation, skewing, stretching, and compressing. Each transformation has its own rules and formulas that determine how the function is affected.
- Translation: This transformation involves shifting the entire function horizontally or vertically. The function moves without changing its shape or orientation.
- Reflection: In this transformation, the function is flipped over a line of reflection. The shape and orientation of the function are reversed.
- Dilation: Dilation changes the size of the function by stretching or compressing it. The function expands or contracts, but its shape and orientation remain the same.
- Rotation: Rotation involves rotating the function around a fixed point. The function turns but keeps its shape and size.
- Skewing: Skewing slants the function in a diagonal direction. It distorts the shape and orientation of the function.
- Stretching: This transformation stretches the function vertically or horizontally. The function becomes taller or wider, but its shape remains the same.
- Compressing: Compressing squeezes the function vertically or horizontally. The function becomes shorter or narrower, but its shape stays the same.
By mastering these seven transformations, we can analyze, graph, and manipulate linear functions with ease. They provide powerful tools for solving problems and understanding the behavior of linear functions in various contexts.