In geometry, congruent triangles are triangles that have exactly the same shape and size. There are several methods to prove that two triangles are congruent, including the Side-Side-Side (SSS) and Side-Angle-Side (SAS) congruence criteria. These criteria provide a set of conditions that guarantee that two triangles are congruent.
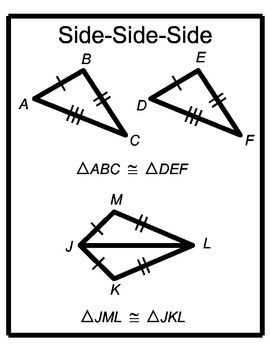
For the SSS congruence criterion, three sides of one triangle must be equal to the corresponding sides of another triangle. This means that if the lengths of the three sides of two triangles are equal, then the two triangles are congruent. The SSS criterion is often used in solving problems involving congruent triangles, and it helps establish equal measures between corresponding angles and sides.
On the other hand, the SAS congruence criterion requires that two sides and the included angle of one triangle are equal to the corresponding sides and included angle of another triangle. This means that if the lengths of two sides and the measure of the included angle of two triangles are equal, then the two triangles are congruent. The SAS criterion allows us to determine congruence when we have a common side or angle.
Understanding and applying the concepts of SSS and SAS congruence criteria are essential in solving geometry problems involving congruent triangles. By using these criteria, we can confidently determine that two triangles have the same shape and size, making it easier to solve problems related to side and angle measurements, and ultimately, improve our overall geometry skills.
What is 4 4 SSS and SAS Homework?
In mathematics, SSS and SAS are abbreviations used to describe the properties of triangles. These abbreviations stand for Side-Side-Side and Side-Angle-Side, respectively. The 4 4 SSS and SAS Homework refers to a specific homework assignment that focuses on these two types of triangles and their corresponding properties.
The SSS property states that if the lengths of three sides of a triangle are equal to the corresponding sides of another triangle, then the two triangles are congruent. In other words, if all three sides of one triangle are equal to the corresponding sides of another triangle, the two triangles will have the same shape and size.
The SAS property, on the other hand, states that if two sides and the included angle of one triangle are equal to the corresponding sides and included angle of another triangle, then the two triangles are congruent. This means that if the lengths of two sides and the angle between them in one triangle are equal to the lengths of two sides and the angle between them in another triangle, the two triangles will be congruent.
The 4 4 SSS and SAS Homework assignment would likely involve problems and exercises that require students to identify congruent triangles using the SSS and SAS properties. Students might be asked to determine if two given triangles are congruent based on the lengths of their sides and angles, or to find missing side lengths or angles of triangles using congruence statements.
Overall, the 4 4 SSS and SAS Homework is an opportunity for students to practice applying the SSS and SAS properties to solve problems involving congruent triangles. It helps build their understanding of triangle congruence and prepares them for more advanced concepts in geometry.
Understanding the concept of SSS and SAS in Geometry
In geometry, SSS and SAS are two important concepts that are used to prove the congruence of triangles. SSS stands for Side-Side-Side, which means that if three sides of one triangle are congruent to three sides of another triangle, then the two triangles are congruent. SAS, on the other hand, stands for Side-Angle-Side, which means that if two sides and the included angle of one triangle are congruent to two sides and the included angle of another triangle, then the two triangles are congruent.
To better understand these concepts, let’s look at some examples. Say we have triangle ABC and triangle DEF. If we know that AB is congruent to DE, BC is congruent to EF, and AC is congruent to DF, then we can conclude that triangle ABC is congruent to triangle DEF by the SSS congruence theorem. This means that all corresponding angles and sides of the triangles are congruent.
In another example, let’s say we have triangle PQR and triangle STU. If we know that PQ is congruent to ST, QR is congruent to TU, and angle PQR is congruent to angle STU, then we can conclude that triangle PQR is congruent to triangle STU by the SAS congruence theorem. Again, this means that all corresponding angles and sides of the triangles are congruent.
These concepts are fundamental to geometry and are used in various geometric proofs and constructions. They help us understand and analyze the congruence of triangles, which is important in solving problems involving triangles and their properties.
Importance of SSS and SAS Homework Answer Key
When studying geometry and completing homework assignments, it is crucial to have access to the SSS (Side-Side-Side) and SAS (Side-Angle-Side) homework answer key. These two postulates are fundamental in proving congruence between triangles, and understanding them is essential for success in geometry.
With the SSS postulate, students are able to determine if two triangles are congruent by comparing the lengths of their corresponding sides. Being able to identify congruent triangles helps in solving various geometry problems and proofs. The SSS homework answer key provides students with a guide to check their work and verify if the given sides of the triangles are congruent.
Similarly, the SAS postulate allows students to determine congruence by comparing the measures of the angles and the lengths of the sides. Having access to the SAS homework answer key allows students to check their work and ensure that they have correctly applied the postulates to prove congruence between triangles.
Having an answer key for SSS and SAS homework is beneficial for students as it provides them with immediate feedback on their understanding of these crucial postulates. It allows them to identify and rectify any mistakes they might have made, enabling them to grasp the concepts more effectively.
Furthermore, the SSS and SAS postulates are building blocks for more complex concepts in geometry, such as the HL (Hypotenuse-Leg) postulate and the ASA (Angle-Side-Angle) postulate. By mastering SSS and SAS, students lay a strong foundation for further geometry studies.
In conclusion, the SSS and SAS homework answer key plays a vital role in helping students understand and apply these postulates correctly. It provides them with immediate feedback, helps them identify mistakes, and strengthens their foundation in geometry. Access to these answer keys is essential for students to excel in their geometry studies and build a solid understanding of congruence in triangles.
Tips for Solving 4 4 SSS and SAS Homework Problems

Solving 4 4 SSS (Side-Side-Side) and SAS (Side-Angle-Side) homework problems can sometimes be challenging, but with the right approach and some helpful tips, you can successfully tackle them. Here are some strategies to consider:
1. Identify the Given Information
Before attempting to solve the problem, carefully read the question and identify the given information. Look for any side lengths or angles that are provided. This step is crucial as it helps you understand what is known and what needs to be found.
2. Determine Which Theorem or Postulate to Apply

In 4 4 SSS and SAS problems, you will typically use the SSS or SAS congruence postulate. Determine which postulate applies based on the given information. If you have three side lengths, you can use the SSS postulate. If you have two side lengths and the included angle, you can use the SAS postulate.
3. Set Up the Congruence Statement
Once you have identified the postulate to apply, set up the congruence statement. This statement should compare the corresponding sides and angles of the two triangles. Write it in the form “Triangle ABC is congruent to Triangle XYZ” and include the corresponding parts that are congruent to each other.
4. Solve for the Unknown
Using the congruence statement, you can now solve for the unknown side lengths or angles. Use any necessary algebraic steps or geometric properties to find the missing values. Remember to show all your steps and reasoning.
5. Check Your Solution
After finding the unknowns, it is essential to check your solution. Make sure that all the given information is consistent with the congruence statement. Check for any calculation errors and ensure that the solution makes logical sense within the context of the problem.
By following these tips, you can approach and solve 4 4 SSS and SAS homework problems with confidence and accuracy. Practice applying these strategies to various problems to improve your problem-solving skills in geometry.
Identifying the given information
In geometry, when solving problems using the SSS (Side-Side-Side) and SAS (Side-Angle-Side) methods, it is crucial to accurately identify the given information. This information serves as the basis for finding missing side lengths or angles in a triangle.
SSS Method:
- When using the SSS method, you are given the lengths of all three sides of a triangle.
- For example, a problem might state that side AB is 6 cm, side BC is 8 cm, and side AC is 10 cm.
- These side lengths allow you to determine the size and shape of the triangle.
SAS Method:
- When using the SAS method, you are given two sides of a triangle and the angle between them.
- For example, a problem might state that side AB is 5 cm, side BC is 7 cm, and angle ABC is 45 degrees.
- With these measurements, you can determine the size and shape of the triangle.
Identifying the given information correctly is crucial, as it allows you to apply the correct geometric principles and formulas to solve the problem. In addition, it helps you determine which method (SSS or SAS) to use when solving the triangle.
Applying the SSS (Side-Side-Side) criteria
In geometry, the SSS (Side-Side-Side) criterion is a way to prove that two triangles are congruent. This criterion states that if the three sides of one triangle are congruent to the corresponding sides of another triangle, then the two triangles are congruent.
To apply the SSS criterion, you need to compare the lengths of the sides of the two triangles. If all three sides of one triangle are equal to the corresponding sides of the other triangle, then you can conclude that the two triangles are congruent. This means that all corresponding angles and sides of the triangles are also equal.
To illustrate how the SSS criterion works, consider the following example: Triangle ABC and Triangle DEF. If side AB is congruent to side DE, side BC is congruent to side EF, and side AC is congruent to side DF, then we can apply the SSS criterion to prove that Triangle ABC is congruent to Triangle DEF.
Using the SSS criterion, we can establish a strong foundation for solving geometric problems. By carefully analyzing the lengths of the sides of triangles, we can determine when two triangles are congruent, which can be useful in various applications of geometry, such as finding missing angles or solving real-life problems involving shapes and figures.
Applying the SAS (Side-Angle-Side) criteria

The SAS criteria, which stands for Side-Angle-Side, is a method used to determine whether two triangles are congruent. In order for two triangles to be congruent using the SAS criteria, they must have the same lengths of two sides and the same measurement of the included angle between those sides.
When applying the SAS criteria, it is important to first identify the two sides that are congruent in both triangles. These sides are called the corresponding sides. Once the corresponding sides are identified, the next step is to determine if the included angles between those sides are congruent as well. If the lengths of the two corresponding sides and the angle between them are all congruent, then the triangles are congruent using the SAS criteria.
For example, imagine we have Triangle ABC and Triangle DEF. We know that side AB is congruent to side DE and side AC is congruent to side DF. Additionally, we know that angle A is congruent to angle D. By applying the SAS criteria, we can conclude that Triangle ABC is congruent to Triangle DEF.
In summary, the SAS criteria is a useful method for determining triangle congruence. By comparing the lengths of two sides and the included angle between them, we can determine whether two triangles are congruent. Understanding and applying the SAS criteria is essential in geometry and can help in solving various geometric problems and proofs.
Checking for Congruence
Congruent figures have the same size and shape. They can be flipped, rotated, or slid without changing their overall appearance. When determining if two figures are congruent, there are several methods that can be used to check for congruence.
Side-Side-Side (SSS) is a method used to determine congruence by comparing the lengths of corresponding sides. If all three pairs of corresponding sides are equal, then the figures are congruent. This method relies on the fact that corresponding sides in congruent figures are in the same proportion. For example, if triangle ABC and triangle DEF have sides AB = DE, BC = EF, and AC = DF, then the two triangles are congruent.
Side-Angle-Side (SAS) is another method used to determine congruence. In this method, the lengths of two sides and the measure of the included angle are compared. If two pairs of corresponding sides are equal and the included angles are congruent, then the figures are congruent. For example, if triangle ABC has sides AB = DE, BC = EF, and angle BAC = angle DFE, then triangle ABC is congruent to triangle DEF.
In addition to these methods, there are also other ways to check for congruence, such as Angle-Angle-Side (AAS), Hypotenuse-Leg (HL), and right-angled triangles. Each method has its own set of conditions that must be satisfied in order to determine congruence.
Overall, checking for congruence requires comparing corresponding sides and angles of two figures to determine if they have the same size and shape. By using methods like SSS and SAS, one can easily determine if two figures are congruent or not.
Table:
| Method | Conditions for Congruence |
|---|---|
| SSS | All three pairs of corresponding sides are equal. |
| SAS | Two pairs of corresponding sides are equal and the included angles are congruent. |
| AAS | Two pairs of corresponding angles are equal and the included side is equal. |
| HL | The hypotenuse and one leg of a right-angled triangle are equal to the corresponding parts of another right-angled triangle. |