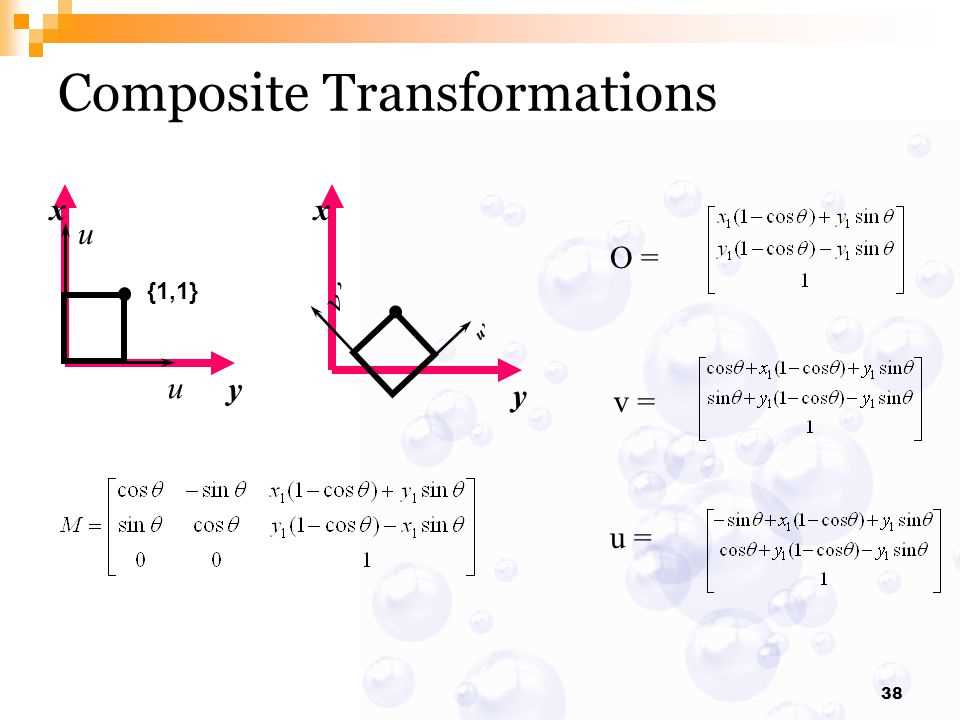
In the field of geometry and mathematics, understanding the composition of transformations is essential. Transformations involve the manipulation of shapes and figures through various operations such as translations, rotations, reflections, and dilations. The composition of transformations refers to the process of combining two or more transformations to create a new transformation. This concept is important because it allows us to understand how multiple transformations can affect the position, size, and orientation of an object.
The composition of transformations can be a complex topic for students to grasp, as it requires a solid understanding of each individual transformation and how they interact with one another. To aid in the learning process, teachers often provide composition of transformations worksheets to reinforce these concepts. These worksheets typically include a series of transformation problems that students must solve by following a set of rules and guidelines.
When completing a composition of transformations worksheet, students need to apply the correct order of operations. This means they must perform each transformation step by step, in the correct sequence. For example, if a problem involves a translation followed by a rotation, students need to first perform the translation and then the rotation, taking into account the specific instructions given. By following the correct order of operations, students can accurately determine the final position, size, and orientation of the transformed object.
Understanding the Composition of Transformations: Worksheet Answers
The composition of transformations is an important concept in geometry that involves applying multiple transformations to an object. This process allows us to manipulate and analyze shapes in various ways. The worksheet provided helps students practice their understanding of composition by applying different transformations to objects and determining the final position or properties of the shape.
The answers to the worksheet require a strong grasp of the different types of transformations, including translations, rotations, reflections, and dilations. By correctly identifying the sequence of transformations and their corresponding properties, students can determine the final shape or position of the object. It is important to carefully analyze each step and consider how each transformation affects the shape in order to arrive at the correct solution.
The worksheet may include questions that involve combining multiple transformations, such as first rotating a shape and then reflecting it across a line. These types of tasks require students to understand the order of operations and how each transformation impacts the shape differently. It also emphasizes the importance of understanding the properties of each transformation and how they affect the object’s position, size, and orientation.
To correctly answer the worksheet, students should also be familiar with the properties of different geometric figures. This includes understanding the symmetry properties of shapes and how they are preserved or altered through transformations. By applying their knowledge of geometric properties, students can accurately determine the final position or properties of the transformed shape.
In conclusion, understanding the composition of transformations is an essential skill in geometry. The worksheet answers help students practice this skill by applying different transformations and analyzing the effects on geometric objects. By carefully considering the properties of each transformation and the order in which they are applied, students can successfully determine the final shape or position of a transformed object.
Exploring the Basic Concepts of Transformations
Transformations are fundamental concepts in mathematics and geometry that involve changing the position, size, or shape of an object. In geometry, there are four basic types of transformations: translation, rotation, reflection, and dilation. Each of these transformations has its own unique properties and can be used to manipulate objects in different ways.
Translation: A translation is a type of transformation that moves every point of an object in a certain direction and distance without changing its shape or orientation. It is like sliding an object along a plane. In a translation, each point of the object is moved by the same distance and in the same direction.
Rotation: Rotation is a transformation that turns an object around a fixed point called the center of rotation. The object is rotated by an angle measured in degrees, either clockwise or counterclockwise. The shape and size of the object remain unchanged, only its orientation is altered.
Reflection: Reflection is a transformation that flips an object over a line called the line of reflection. It creates a mirror image of the object, where each point on one side of the line is mirrored onto the other side. Reflection can occur horizontally, vertically, or diagonally.
Dilation: Dilation is a transformation that changes the size of an object. It involves stretching or shrinking the object by a scale factor, which can be greater than 1 (expanding) or between 0 and 1 (contracting). The shape and orientation of the object remain the same, only its size changes.
By understanding these basic concepts of transformations, mathematicians and scientists can apply them to solve problems in various fields, such as engineering, computer graphics, and physics. Transformations play a crucial role in areas such as image processing, pattern recognition, and animation, allowing us to manipulate and visualize objects in a virtual environment.
Identifying Types of Transformations
When working with transformations, it is important to be able to identify the type of transformation that is being used. There are several common types of transformations that can be encountered, each with its own characteristics. By understanding these types, we can better analyze and solve problems related to transformations.
One type of transformation is translation. This involves moving an object from one location to another without changing its shape or orientation. In a translation, all points of the object move by the same distance and direction. This is often represented as (x + a, y + b), where (a, b) represents the distance and direction of the translation.
Another type of transformation is reflection. This involves flipping an object across a line of reflection, often a horizontal or vertical line. When reflecting an object, all points on one side of the line are reflected to the opposite side, while maintaining their distance from the line. This is often represented as (x, -y) or (-x, y).
Rotation is another common type of transformation. This involves turning an object around a fixed point, known as the center of rotation. The object is rotated by a certain angle in a clockwise or counterclockwise direction. The angle of rotation can be specified as a positive or negative value. This is often represented as (x*cosθ – y*sinθ, x*sinθ + y*cosθ), where (x, y) represents the coordinates of the original object and θ represents the angle of rotation.
Finally, there is scaling, which involves changing the size of an object. Scaling can be uniform, where the object is enlarged or reduced by a consistent factor in all directions, or non-uniform, where different factors are applied to different directions. Scaling is often represented as (kx, ky), where k represents the scale factor.
In summary, being able to identify the type of transformation being used is essential in understanding and solving problems related to transformations. Whether it is a translation, reflection, rotation, or scaling, each type has its own distinct characteristics that can help guide our analysis and calculations.
Applying the Transformation Rules
When working with transformations in mathematics, it is important to understand and apply the transformation rules correctly. These rules dictate how a geometric shape can be transformed through translation, reflection, rotation, and dilation. By following these rules, we can accurately describe the new position, orientation, and size of the shape after the transformation.
The first rule to remember is the translation rule. This rule states that every point in a shape is shifted by a certain amount in the x and y directions. For example, if we want to translate a shape 3 units to the right and 2 units up, we would add 3 to the x-coordinates and 2 to the y-coordinates of each point. This rule allows us to move the shape without changing its orientation or size.
Another important rule is the reflection rule. This rule states that every point in a shape is mirrored across a line or axis of reflection. To reflect a shape across the x-axis, for example, we would change the sign of the y-coordinates of each point. This rule allows us to create a mirror image of the shape without changing its position or size.
The rotation rule is used to rotate a shape around a given point. This rule states that every point in the shape is rotated by a certain angle around the given point. To rotate a shape 90 degrees clockwise, for instance, we would use the following formulas:
x’ = x*cos(angle) – y*sin(angle)
y’ = x*sin(angle) + y*cos(angle)
These formulas allow us to change the orientation of the shape without changing its position or size.
Lastly, the dilation rule is used to scale a shape up or down. This rule states that every point in a shape is multiplied by a certain scale factor. To dilate a shape by a scale factor of 2, for instance, we would multiply the x-coordinates and y-coordinates of each point by 2. This rule allows us to increase or decrease the size of the shape without changing its position or orientation.
Solving Transformation Problems
When it comes to solving transformation problems, it is important to have a clear understanding of the different types of transformations and how they can be combined. This knowledge will help you approach problems with confidence and find the most efficient solution.
One of the key aspects of solving transformation problems is understanding the order of operations. Just like in algebra, the order in which transformations are applied can make a big difference in the final result. It is important to carefully read the problem and determine the correct sequence of transformations.
Another important skill for solving transformation problems is being able to visualize the effects of each transformation. It can be helpful to sketch out the original figure and then apply each transformation step by step. This will give you a clearer picture of how the figure is being transformed and make it easier to find the final result.
When encountering more complex problems, it can be useful to break them down into smaller, more manageable steps. For example, if you are asked to find the composition of several transformations, you can first find the result of each individual transformation and then combine them together. This approach can help simplify the problem and make it easier to solve.
In conclusion, solving transformation problems requires a solid understanding of the different types of transformations, order of operations, and the ability to visualize the effects of each transformation. With these skills, you can approach problems confidently and find efficient solutions.
“`html
Analyzing Real-World Scenarios
In real-world scenarios, understanding the composition of transformations can help us analyze and solve various problems. For example, let’s consider a scenario where a company wants to optimize its delivery routes to minimize time and cost. By applying transformations such as translation, rotation, and scaling, the company can analyze the current routes and find ways to improve efficiency. They can translate the routes to different locations to reduce travel distance, rotate the routes to avoid traffic congestion, or scale the routes to accommodate changes in demand.
Another real-world scenario where analyzing the composition of transformations is important is in digital image processing. For instance, when editing a photo, various transformations like rotation, scaling, and cropping are applied to achieve the desired result. By understanding how these transformations interact and can be combined, we can manipulate the image effectively. We can rotate the image to adjust its orientation, scale it to change its size, and crop it to remove unwanted elements.
Some examples of real-world scenarios involving composition of transformations include:
- Architects using transformations to design and visualize buildings.
- Game developers applying transformations to create immersive environments and characters.
- Pilots using transformations to navigate and plot flight paths.
- Artists using transformations to create visually appealing and unique artwork.
“`
Examining the Relationship Between Transformations and Coordinates
Throughout this article, we have explored the concept of transformations and how they relate to coordinates. By applying different transformations to a given set of coordinates, we can alter their position, orientation, and scale in the Cartesian plane.
We have discussed various types of transformations, including translations, rotations, reflections, and dilations. Each transformation can be described using a specific set of rules, such as shifting the coordinates by a certain amount or rotating them around a fixed point. These rules allow us to manipulate the coordinates and visualize the resulting changes in the Cartesian plane.
By understanding the relationship between transformations and coordinates, we can solve problems involving geometric figures, such as finding the image of a shape after a series of transformations or determining the necessary transformations to obtain a desired image. This knowledge is particularly useful in fields such as computer graphics, where transformations are often used to create realistic and visually appealing images.
In conclusion, studying the composition of transformations and their relationship to coordinates provides us with a powerful tool for analyzing and manipulating geometric figures. By applying various transformations, we can transform a given set of coordinates into different positions, orientations, and scales. This knowledge opens up a wide range of possibilities for solving problems and creating visually engaging graphics.
Q&A:
What are transformations in geometry?
Transformations in geometry are operations that change the position, orientation, or size of a figure while preserving its shape. Common transformations include translation, rotation, reflection, and dilation.
How do transformations affect coordinates?
Transformations can change the coordinates of points in a figure. For example, a translation shifts all the points in a figure by a fixed distance in a given direction. A rotation changes the angle of a point with respect to a fixed point. A reflection flips a point across a line of symmetry. A dilation changes the distance between a point and a fixed point.
What is the relationship between transformations and coordinates in geometry?
The relationship between transformations and coordinates in geometry is that transformations can be described and analyzed using coordinate notation. Coordinate notation assigns coordinates to the points in a figure, and transformations can then be described as changes in those coordinates. For example, a translation can be represented as (x, y) → (x + a, y + b), where a and b represent the distances of the translation in the x and y directions respectively.
Why is understanding the relationship between transformations and coordinates important?
Understanding the relationship between transformations and coordinates is important in geometry because it allows us to describe and analyze geometric transformations using a mathematical framework. This framework enables us to make precise and accurate calculations and predictions about how figures will change under different transformations. It also helps us to understand and solve real-world problems that involve spatial relationships and transformations.