****
Geometry is a branch of mathematics that deals with the properties, measurement, and relationships of points, lines, angles, surfaces, and solids. It is a fundamental subject that plays a vital role in understanding and analyzing the world around us. Unit 6 of a geometry course typically focuses on topics such as polygons, circles, and three-dimensional figures.
As geometry can sometimes be challenging, having the correct answer key for review purposes is essential. This article provides the answer key for Unit 6 of a geometry course, allowing students to check their work, understand the correct solutions, and reinforce their understanding of the mathematical concepts covered in the unit.
The answer key for Unit 6 includes solutions and explanations for various types of problems, such as finding the area and perimeter of polygons, calculating the circumference and area of circles, identifying different types of angles and triangles, and determining the volume and surface area of three-dimensional figures. This comprehensive answer key acts as a valuable resource for students to test their knowledge, identify areas for improvement, and consolidate their understanding before assessments or exams.
Geometry Unit 6 Review Answer Key
Congratulations on completing Unit 6 of your geometry course! Now it’s time to review and check your understanding. Below you will find the answer key to the Unit 6 review worksheet, which will help you assess your knowledge and identify any areas that may require additional practice.
1. The first question on the review worksheet asks you to determine the missing angle measure in a triangle. The correct answer is 60 degrees. To find this, you can use the fact that the sum of the interior angles of a triangle is always 180 degrees.
| Angle 1 | Angle 2 | Angle 3 |
|---|---|---|
| 90 degrees | 30 degrees | ? |
2. The second question involves finding the length of a particular line segment in a given figure. The correct answer is 8 units. This can be found by applying the Pythagorean theorem, which states that in a right triangle, the square of the length of the hypotenuse is equal to the sum of the squares of the lengths of the other two sides.
3. In the third question, you are asked to classify a pair of angles based on their measures. The correct answer is “complementary.” Two angles are considered complementary when their measures add up to 90 degrees. In this case, Angle 1 is 40 degrees and Angle 2 is 50 degrees, so they are complementary.
- Angle 1: 40 degrees
- Angle 2: 50 degrees
4. The fourth question involves finding the volume of a rectangular prism. The correct answer is 216 cubic units. To find the volume of a rectangular prism, you multiply its length, width, and height. In this case, the length is 6 units, the width is 3 units, and the height is 12 units.
By referring to this answer key, you can check your work and gain a better understanding of the concepts covered in Unit 6. Remember to review any topics where you made mistakes or struggled, as this will help solidify your understanding and prepare you for future geometry challenges.
Understanding Transformations
A transformation in geometry refers to an operation that changes the position, shape, or size of a figure. It involves moving or flipping the figure in various ways, such as translations, reflections, rotations, and dilations. These transformations play a crucial role in understanding the properties and relationships of geometric figures.
Translations involve moving a figure from one location to another without changing its shape or size. This can be done by sliding the figure along a given vector or direction. Translations are often represented using coordinates and vectors, helping to determine the new position of each point.
Reflections occur when a figure is flipped or mirrored over a line, known as the line of reflection. This line acts as a mirror, with each point on the figure having a corresponding point on the other side. Reflections are important in symmetry analysis and can be described using the coordinates of the original figure and the line of reflection.
Rotations involve rotating a figure around a point, known as the center of rotation, by a specified angle. This causes each point of the figure to move in a circular path, creating a new position. Rotations play a key role in understanding angles, orientation, and symmetry in geometric figures.
Dilations are transformations that change the size of a figure without altering its shape. This is achieved by stretching or shrinking the figure from a fixed center, known as the center of dilation. Dilations are characterized by a scale factor, which determines the ratio of the new figure’s dimensions to the original figure’s dimensions.
To fully understand transformations, it is crucial to learn and apply the mathematical concepts, algorithms, and formulas associated with each type. Working with geometric figures and using transformational methods can help develop spatial reasoning skills and improve problem-solving abilities in geometry.
Solving Problems with Similarity
Solving problems with similarity involves applying geometric concepts and techniques to determine the relationships between similar figures and solve for unknown quantities. These problems often require an understanding of proportional relationships and the properties of similar triangles and other similar polygons.
One common approach to solving similarity problems is using the concept of corresponding sides and angles. In similar figures, corresponding angles are congruent and corresponding sides are proportional. By identifying corresponding angles and sides, we can set up proportion equations to solve for unknown values. For example, if we have two similar triangles, we can set up the proportion equation: $frac{AB}{DE} = frac{BC}{EF}$, where AB and DE are corresponding sides and BC and EF are corresponding sides. By solving this equation, we can find the value of the unknown side length.
Example:
Given that triangle ABC is similar to triangle DEF, with AB = 4 cm, BC = 6 cm, and DE = 5 cm, find the length of side EF.
To solve this problem, we can set up the proportion equation $frac{AB}{DE} = frac{BC}{EF}$ and plug in the given values:
$frac{4}{5} = frac{6}{EF}$
Next, we can cross-multiply and solve for EF:
$4 cdot EF = 6 cdot 5 implies EF = 7.5$
Therefore, the length of side EF is 7.5 cm.
In addition to solving for unknown side lengths, problems involving similarity can also require finding missing angles. This can be done using the property that corresponding angles in similar figures are congruent. By identifying corresponding angles and setting up proportion equations, we can solve for unknown angles using algebraic methods.
Overall, solving problems with similarity involves using geometric concepts and techniques to determine relationships between similar figures and solve for unknown quantities. By applying proportion equations and identifying corresponding angles and sides, we can find missing side lengths and angles in similar figures.
Exploring Right Triangle Trigonometry

Right triangle trigonometry is a branch of mathematics that focuses on the relationships between the angles and sides of right triangles. It is an essential tool for solving problems in various fields such as engineering, physics, and architecture. By understanding and applying right triangle trigonometry, we can calculate unknown angles or side lengths using the trigonometric ratios sine, cosine, and tangent.
The sine of an angle in a right triangle is defined as the ratio of the length of the side opposite the angle to the length of the hypotenuse. It is denoted as sin(theta). The cosine of an angle is defined as the ratio of the length of the adjacent side to the length of the hypotenuse, denoted as cos(theta). Finally, the tangent of an angle is defined as the ratio of the length of the opposite side to the length of the adjacent side, denoted as tan(theta). These ratios are fundamental in right triangle trigonometry and allow us to calculate unknown values in a right triangle.
When exploring right triangle trigonometry, it is important to understand the relationships between the angles and sides of a right triangle. The Pythagorean theorem states that in a right triangle, the square of the length of the hypotenuse is equal to the sum of the squares of the lengths of the other two sides. This theorem is key in solving for unknown side lengths in a right triangle.
The mnemonic “SOHCAHTOA” is commonly used to help remember the trigonometric ratios. “SOH” represents sine, “CAH” represents cosine, and “TOA” represents tangent. By memorizing this mnemonic, we can easily recall the trigonometric ratios and their respective definitions. This aids us in solving problems involving right triangle trigonometry.
In conclusion, right triangle trigonometry is a powerful tool for solving problems involving right triangles. By understanding the relationships between angles and sides, and using the trigonometric ratios sine, cosine, and tangent, we can calculate unknown values and solve real-world problems in various fields of study.
Analyzing Properties of Quadrilaterals

Quadrilaterals are four-sided polygons that have unique properties and characteristics. By analyzing these properties, we can classify and understand different types of quadrilaterals.
One important property of quadrilaterals is that the sum of its interior angles is always equal to 360 degrees. This means that no matter what type of quadrilateral we have, the total measure of all its angles will add up to 360 degrees.
Another property to consider is the opposite sides of a quadrilateral. In a parallelogram, for example, the opposite sides are equal in length and parallel to each other. This property allows us to identify quadrilaterals such as rectangles, squares, and rhombi, which have specific angle and side properties based on their opposite sides.
Diagonals also play an important role in analyzing the properties of quadrilaterals. For example, in a kite, the diagonals are perpendicular and one of the diagonals bisects the other at a right angle. This property allows us to identify and differentiate kites from other types of quadrilaterals.
Understanding and analyzing the properties of quadrilaterals is essential in geometry. By studying the angles, sides, diagonals, and other unique characteristics of quadrilaterals, we can accurately classify and solve problems related to these geometric figures.
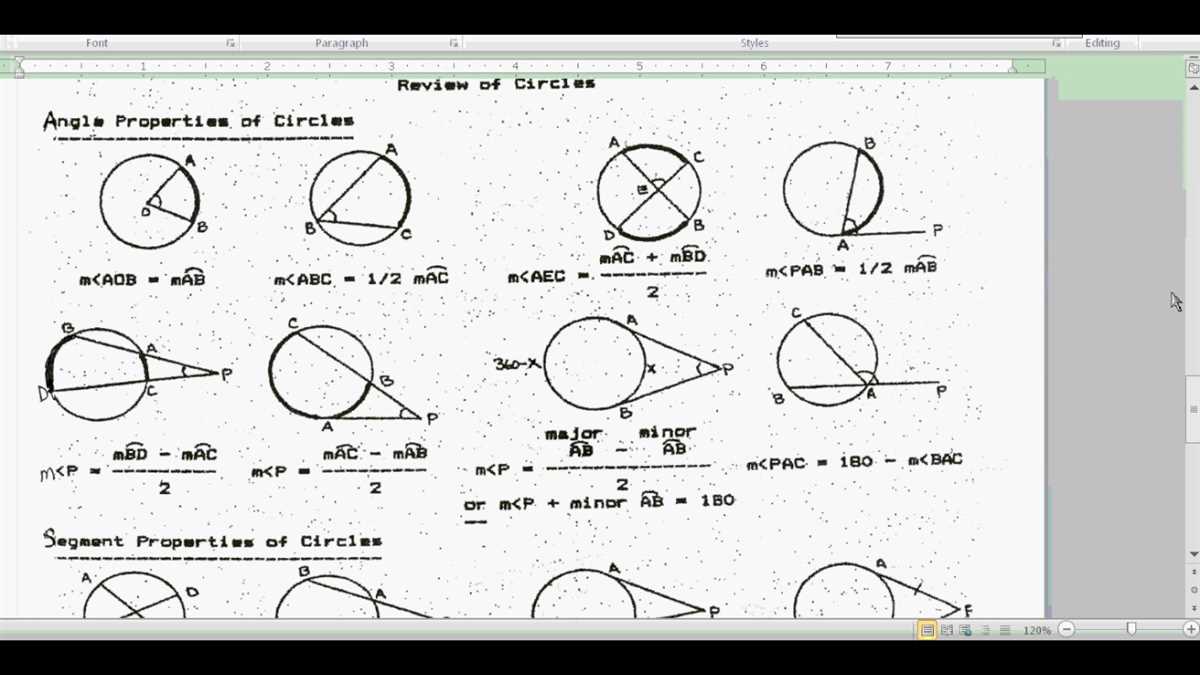
Investigating Circles and Arcs
Circles are an important topic in geometry, and understanding their properties and relationships can help us solve a variety of problems. In this review, we will be investigating circles and arcs to review the key concepts and formulas associated with them.
Circle: A circle is a closed curve in which every point is equidistant from the center. The distance from the center to any point on the circle is called the radius, and the distance across the circle passing through the center is called the diameter.
Arc: An arc is a part of the circle’s circumference. It is defined by two points on the circle and the measure of the central angle between them. Arcs can be classified into different types, such as minor arc, major arc, or semicircle, depending on their length.
In order to find the measures of arcs and angles within circles, we need to understand the different formulas and theorems related to them. Some of the key formulas we will be reviewing include:
- The circumference of a circle: C = 2πr
- The area of a circle: A = πr^2
- The measure of a central angle: α = βθ, where α is the measure of the central angle, β is the ratio of the length of the arc to the circumference, and θ is the measure of the angle in radians.
By understanding and applying these formulas, we will be able to solve problems involving circles and arcs, such as finding the length of an arc, the measure of an angle, or the area of a sector. Practice with these concepts and formulas will strengthen our understanding of geometry and enable us to confidently solve more complex problems in the future.
Applying Coordinate Geometry
Coordinate geometry is a valuable tool in mathematics that allows us to explore geometric concepts using numerical coordinates. By assigning numbers to points on a graph, we can analyze shapes, equations, and relationships in a visual and quantitative way. In this unit, we have learned various techniques and formulas to solve problems using coordinate geometry.
We began by reviewing the basics of graphing in the coordinate plane and understanding the relationship between the x and y axes. We learned how to plot points, identify their coordinates, and describe their location relative to other points. This knowledge was crucial in later lessons when we went on to study lines and their equations.
Next, we delved into the concept of slope and its significance in understanding the characteristics of lines. We learned how to calculate slope using the formula (y2 – y1)/(x2 – x1) and how to interpret its value in terms of steepness, direction, and relationships between different lines. Slope-intercept form, point-slope form, and standard form were all included as tools to describe lines in different ways.
We then applied our knowledge of lines to solve various types of problems, such as finding equations of lines given certain conditions, determining the slope given two points, and analyzing the intersection of two lines. Throughout these lessons, we utilized our understanding of slope and the graphing capabilities of coordinate geometry to solve problems efficiently.
Overall, coordinate geometry provides a powerful framework for analyzing and solving problems in geometry. It incorporates numerical and visual elements, allowing us to gain a deeper understanding of geometric concepts. By applying the techniques and formulas we have learned in this unit, we are able to confidently tackle a wide range of problems involving lines and shapes on the coordinate plane.