When it comes to analyzing patterns and relationships in data, scatter plots are a valuable tool. Scatter plots visually display the relationship between two variables on a coordinate grid, with one variable represented on the x-axis and the other on the y-axis. This allows us to see if there is a correlation or trend between the variables.
Scatter plots can be used to interpret data and make predictions. One way to interpret a scatter plot is by finding a line of fit, also known as a trend line. A line of fit is a straight line that best represents the overall trend of the data points. It can be used to estimate values for a given set of data.
This scatter plots and lines of fit worksheet answer key provides the answers to a set of questions or exercises related to scatter plots and lines of fit. It is a helpful resource for students or anyone looking to practice their skills in interpreting scatter plots and finding lines of fit.
Key Concepts
The scatter plots and lines of fit worksheet answer key covers several key concepts, including:
- Identifying positive, negative, or no correlation in scatter plots
- Finding the correlation coefficient
- Determining the equation of a line of fit
- Using a line of fit to make predictions
By working through the exercises and using the answer key as a guide, students can develop a better understanding of scatter plots and lines of fit, as well as improve their ability to analyze and interpret data.
Understanding Scatter Plots and Lines of Fit Worksheet Answer Key
In the study of statistics, scatter plots and lines of fit are fundamental tools for analyzing and interpreting data. A scatter plot is a visual representation of a set of data points, where each point represents the values of two variables. These plots are useful for identifying patterns and relationships between variables, as well as for making predictions.
When analyzing a scatter plot, one common technique is to find the line of best fit or the line that most closely represents the data points. This line can be used to make predictions about the values of one variable based on the values of the other variable. The answer key for a scatter plot and lines of fit worksheet provides the correct solutions and explanations for finding and interpreting the lines of fit.
The answer key typically includes steps and calculations, such as finding the slope and y-intercept of the line of best fit using the least squares method. It may also include information on how to determine the correlation coefficient, which measures the strength and direction of the relationship between the variables. Additionally, the answer key may provide examples and sample questions to help students better understand the concepts and apply them to real-world situations.
By using the scatter plots and lines of fit worksheet answer key, students can verify their work and ensure they are correctly interpreting the data. It also allows them to practice their analytical and problem-solving skills, which are essential in the field of statistics. Overall, understanding scatter plots and lines of fit is crucial for accurately analyzing and interpreting data, and the answer key serves as a valuable resource for mastering these concepts.
The Importance of Scatter Plots

Scatter plots are an important tool in data analysis as they allow us to visually examine the relationship between two variables. By plotting each data point as a dot on a graph, we can easily identify patterns, trends, and correlations. This graphical representation helps us make sense of complex data sets and provides valuable insights into the relationship between variables.
Scatter plots are particularly useful in identifying correlations. By visually inspecting the pattern formed by the data points, we can determine whether there is a positive, negative, or no correlation between the variables. This information is crucial in many fields, ranging from medicine to finance, as it allows us to make predictions and decisions based on the observed relationships.
Furthermore, scatter plots can help us identify outliers and anomalies in data sets. By examining the distribution of dots on the graph, we can easily spot any data points that do not align with the general pattern or trend. These outliers may indicate measurement errors, data entry mistakes, or unusual observations that require further investigation. Identifying and understanding outliers is essential for accurate analysis and decision-making.
In addition, scatter plots are often used to fit lines or curves to the data points. This process, known as regression analysis, allows us to create a mathematical model that approximates the relationship between the variables. By fitting a line of best fit, we can make predictions and estimate values for unobserved data points. Regression analysis is a powerful tool in forecasting, trend analysis, and making informed decisions.
Overall, scatter plots play a crucial role in data analysis by providing a visual representation of the relationship between variables, helping us identify correlations and outliers, and enabling regression analysis for prediction and decision-making purposes. By utilizing scatter plots, we can gain valuable insights and make data-driven decisions in various fields.
Explaining Lines of Fit
A line of fit is a straight line that best represents the trend of a scatter plot. It shows the relationship between two sets of data and can be used to make predictions or draw conclusions. In order to find the line of fit, we use the method of linear regression.
Linear Regression: Linear regression is a statistical method used to find the equation of a straight line that best fits a set of data points. It minimizes the vertical distance between the line and the points, and is typically calculated using the least squares method.
Steps to find the line of fit:
- Create a scatter plot of the data.
- Observe the trend of the data. Determine whether the relationship is positive or negative.
- Draw a line that appears to fit the data points well.
- Calculate the slope and y-intercept of the line of fit using linear regression.
- Write the equation of the line of fit in the form y = mx + b, where m is the slope and b is the y-intercept.
The equation of the line of fit can be used to make predictions or estimate values for a given set of data. It can also help to identify outliers or data points that do not fit the trend.
It is important to note that a line of fit is an approximation and may not perfectly represent the data. However, it provides a useful summary of the relationship between the variables and can be a helpful tool in data analysis.
Interpreting Scatter Plots and Lines of Fit
A scatter plot is a visual representation of the relationship between two variables. It displays data points on a graph, with the x-axis representing one variable and the y-axis representing the other variable. By plotting the data points, you can see if there is a correlation or trend between the two variables.
When interpreting a scatter plot, it is important to look for patterns and trends. If there is a positive correlation, the data points will generally rise from left to right. This means that as the x-value increases, the y-value also tends to increase. On the other hand, if there is a negative correlation, the data points will generally fall from left to right. This means that as the x-value increases, the y-value tends to decrease.
Lines of fit are used to summarize the trend in a scatter plot. They are drawn to approximate the relationship between the variables. A line of fit can be used to make predictions or estimate values based on the given data. The equation of the line can also be determined using linear regression.
When analyzing a scatter plot with a line of fit, you can see how well the data points fit the line. If the data points are closer to the line, it suggests a strong correlation. If the data points are more scattered and further away from the line, it suggests a weaker correlation.
In conclusion, scatter plots and lines of fit are valuable tools for interpreting and analyzing the relationship between two variables. They provide visual representation and help to identify patterns, trends, and correlations in the data. By understanding scatter plots and lines of fit, you can make informed decisions and predictions based on the given data.
Using the Scatter Plots and Lines of Fit Worksheet
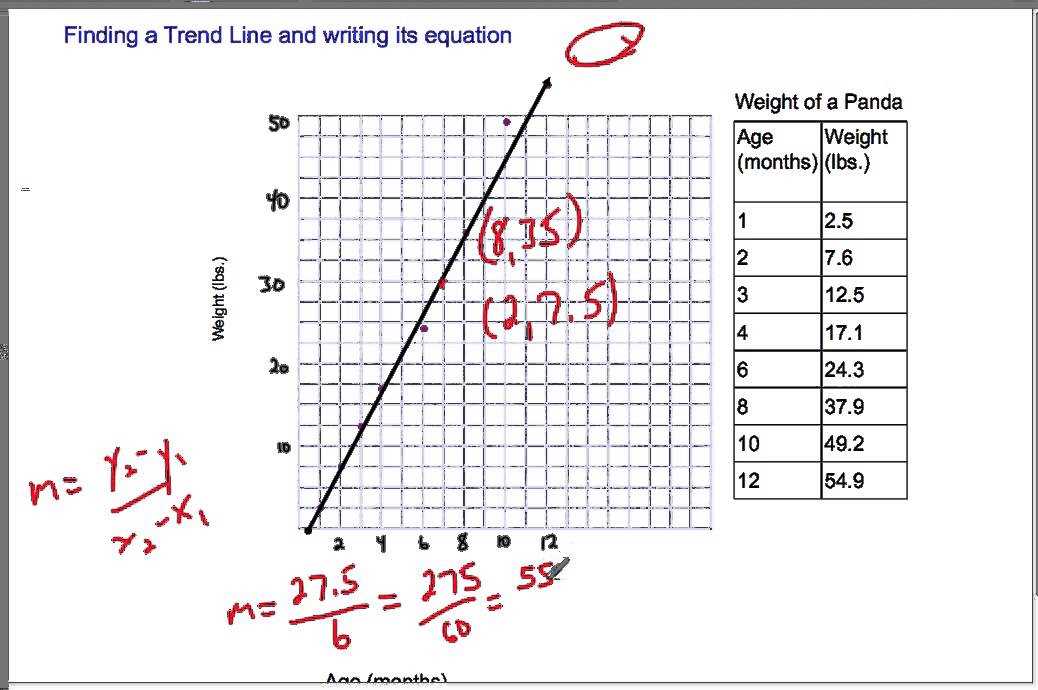
The Scatter Plots and Lines of Fit Worksheet is a valuable tool for analyzing and understanding the relationship between two variables. This worksheet allows students to plot data points on a graph and then draw a line of best fit that represents the overall trend of the data. By completing this worksheet, students can develop their skills in interpreting scatter plots and creating accurate lines of fit.
The Scatter Plots and Lines of Fit Worksheet typically includes a set of data points that need to be plotted on a graph. Students are first instructed to plot each point using the provided x and y values. This allows them to visualize the distribution of the data and identify any patterns or trends. Once the points are plotted, students then draw a line that best represents the overall trend of the data. They can do this by analyzing the general direction and shape of the data points.
One important aspect of the Scatter Plots and Lines of Fit Worksheet is the concept of correlation. The line of best fit represents the correlation between the two variables, which can be positive, negative, or no correlation. Positive correlation means that as one variable increases, the other also tends to increase. Negative correlation means that as one variable increases, the other tends to decrease. No correlation means that there is no apparent relationship between the two variables.
By working through the Scatter Plots and Lines of Fit Worksheet, students can develop their understanding of data analysis and interpretation. They will learn how to identify patterns, draw accurate lines of fit, and interpret the correlation between variables. This worksheet is a valuable tool for building quantitative reasoning skills and preparing students for more advanced statistical analysis in the future.
Analyzing Sample Answers

When analyzing the sample answers for the scatter plots and lines of fit worksheet, it is important to consider the accuracy and completeness of the responses. Students should be able to correctly interpret the data presented in the scatter plots and make informed conclusions.
One key aspect to analyze is whether the students correctly identified the relationship between the variables represented in the scatter plots. They should be able to determine if the relationship is positive, negative, or has no correlation. Additionally, they should be able to explain their reasoning using evidence from the data points.
Another aspect to consider is the students’ ability to determine the line of fit for a given scatter plot. They should understand how to use the data to estimate the best-fit line and identify any outliers. Additionally, they should be able to explain how the line of fit helps to summarize the overall trend of the data.
Furthermore, it is important to assess whether the students accurately calculated slope and y-intercept for the line of fit. They should understand the significance of these values in representing the relationship between the variables. Students should also be able to use the equation of the line of fit to make predictions and estimate values within the given range.
In summary, analyzing sample answers for the scatter plots and lines of fit worksheet involves assessing the accuracy of students’ interpretations, their ability to determine the line of fit, calculate slope and y-intercept, and make predictions based on the given data. The evaluation process should focus on the students’ understanding of these concepts and their ability to apply them effectively.
Tips for Teaching Scatter Plots and Lines of Fit
Teaching scatter plots and lines of fit to students can be a challenging task. However, by employing certain strategies and techniques, educators can effectively convey these concepts to their students. Here are some tips for teaching scatter plots and lines of fit:
- Provide real-world examples: Start by showing students real-world examples of scatter plots and lines of fit. This could include data from sports, weather, or any other relevant context. By making the subject matter relatable, students will be more engaged and motivated to learn.
- Break it down: Break down the process of creating a scatter plot and finding the line of fit into smaller, more manageable steps. Guide students through each step, ensuring that they understand the purpose and significance of each component. This will help them grasp the overall concept more easily.
- Use technology: Utilize technology tools, such as graphing calculators or online graphing software, to create scatter plots and lines of fit. This will give students a hands-on experience and make the learning process more interactive. Additionally, it will provide opportunities for students to explore and analyze data in a visually appealing way.
- Encourage critical thinking: Pose thought-provoking questions to students that require them to think critically about the data and the relationship between variables. This will help them develop their analytical skills and deepen their understanding of scatter plots and lines of fit.
- Provide ample practice: Offer plenty of opportunities for students to practice creating scatter plots and lines of fit. This could include in-class exercises, homework assignments, or even group projects. Repetition and practice are key to solidifying the concepts in students’ minds.
- Offer scaffolding: Provide support to students as they work through the process of creating scatter plots and finding the line of fit. Offer hints, tips, and examples to guide them in the right direction. Gradually remove the scaffolding as students become more comfortable and confident with the material.
In conclusion, teaching scatter plots and lines of fit requires a combination of engaging real-world examples, breaking down the process into smaller steps, utilizing technology, encouraging critical thinking, providing ample practice, and offering scaffolding. By implementing these strategies, educators can help students develop a solid understanding of scatter plots and lines of fit and apply them to real-life situations.