In mathematics, inequalities are expressions that compare values or quantities. They are used to show relationships between numbers and help us understand the relative size of different quantities. Solving inequalities is an important skill in algebra and is often tested in unit assessments.
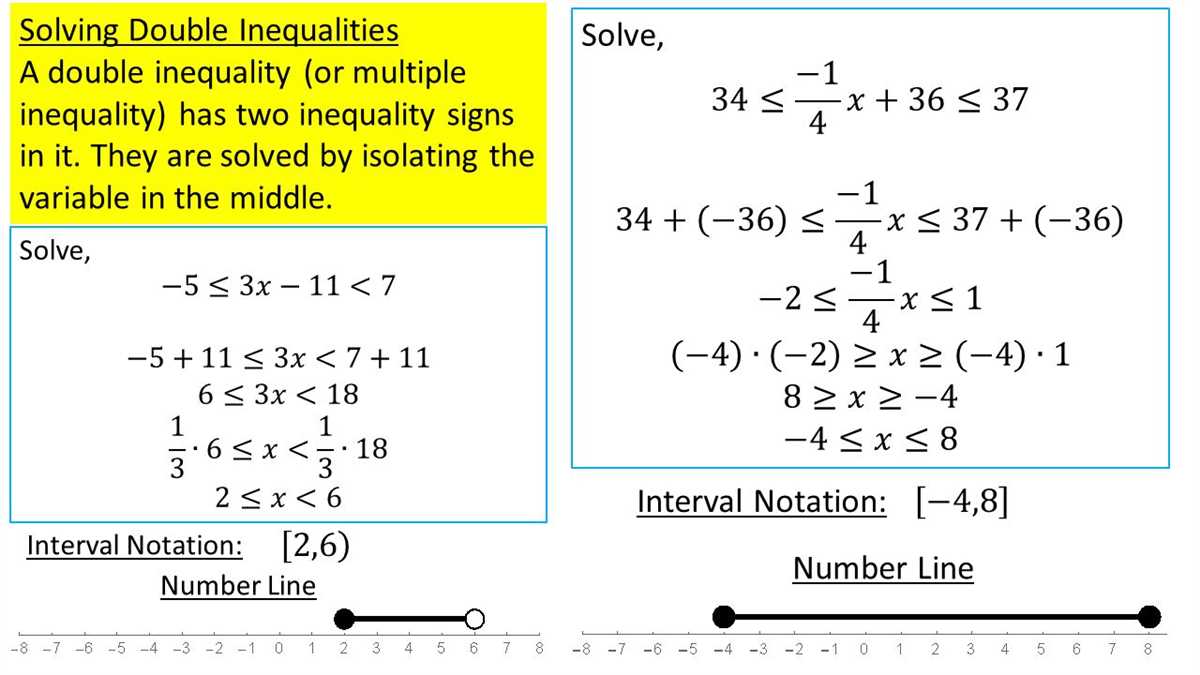
A unit test on solving inequalities typically involves solving and graphing linear inequalities, as well as solving compound inequalities and absolute value inequalities. Students are expected to understand the properties of inequalities and apply various algebraic techniques to solve them. This includes understanding how to solve for variables, simplify expressions, and interpret and graph solutions on a number line.
Unit tests on solving inequalities can be challenging, but they are designed to assess a student’s understanding of key concepts and their ability to apply them. It is important for students to review and practice solving inequalities using different methods, such as graphing, substitution, and interval notation, in order to build confidence and improve their problem-solving skills.
Solving Inequalities Unit Test
If you are taking a math course, chances are you will encounter a unit test on solving inequalities. This test typically assesses your understanding and ability to solve various types of inequalities, such as linear inequalities, quadratic inequalities, absolute value inequalities, and rational inequalities. Inequalities are mathematical expressions that compare two values and indicate a relationship between them. Solving them involves finding the values that satisfy the given conditions and determining the solution set.
During the Solving Inequalities Unit Test, you will be presented with multiple-choice, fill-in-the-blank, and written response questions that require you to apply the concepts and techniques learned in class. It is important to review and understand the properties of inequalities, such as the rules for adding, subtracting, multiplying, and dividing inequalities. You should also be familiar with graphical representations of inequalities on the number line and how to interpret them.
- Linear inequalities: In this section, you will be asked to solve inequalities involving linear equations. This may include solving for x or y, graphing the solution set, or determining whether a given value satisfies the inequality.
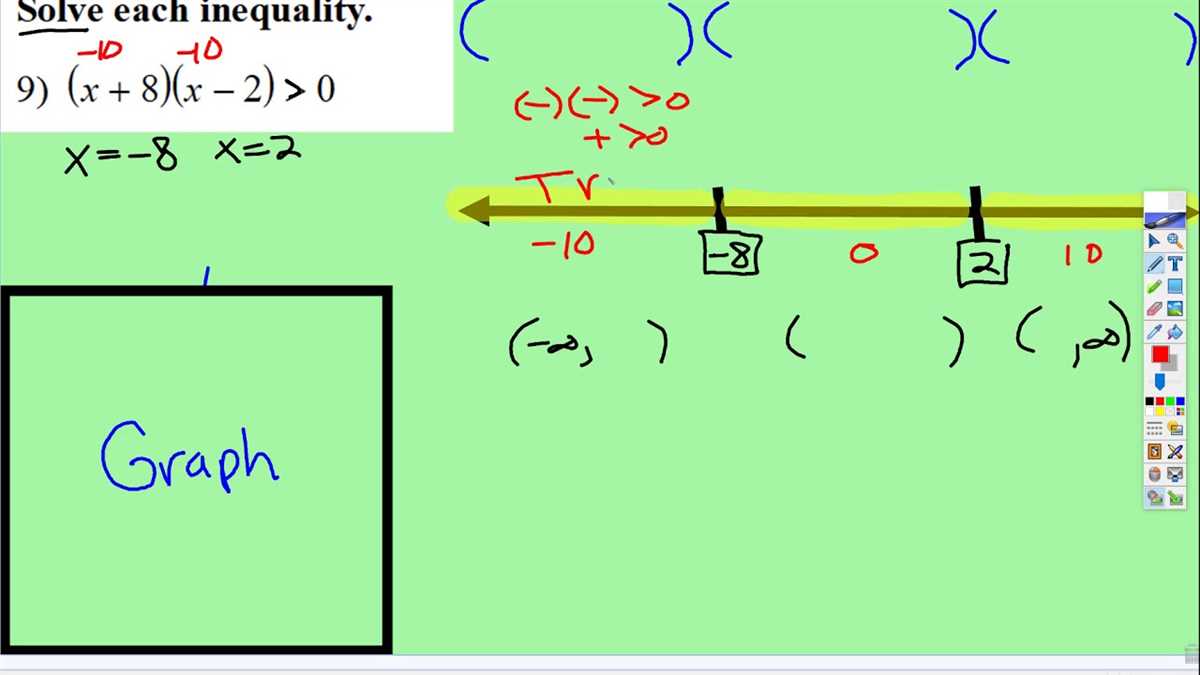
- Quadratic inequalities: This section focuses on solving inequalities involving quadratic equations. You will need to factor the quadratic equation and determine the intervals of values that satisfy the inequality.
- Absolute value inequalities: Absolute value inequalities involve the absolute value function and require you to solve for x within a given range. You will need to consider both positive and negative cases when solving these inequalities.
- Rational inequalities: Rational inequalities involve fractions or rational expressions. You will need to find the critical values that make the numerator or denominator equal to zero and determine the intervals where the inequality holds true.
It is important to thoroughly prepare for the Solving Inequalities Unit Test by reviewing class notes, completing practice problems, and seeking clarification on any challenging concepts. Remember to show all your work and justify your answers to earn maximum credit on the test. Good luck!
What is an inequality?

An inequality is a mathematical statement that compares the values of two expressions using one of the inequality symbols: < (less than), > (greater than), ≤ (less than or equal to), ≥ (greater than or equal to), or ≠ (not equal to). Inequalities indicate a relationship between quantities where one value is larger or smaller than another.
When solving inequalities, the goal is to determine the set of values that satisfy the inequality. This set of values is represented by the solution set. Inequalities can have multiple solutions or no solutions at all, depending on the given parameters and constraints.
Inequalities are commonly used in various fields such as economics, physics, and engineering to represent constraints and conditions. They are also an essential concept in algebra and calculus, where they are used to analyze and solve equations involving variables.
When working with inequalities, it is important to keep in mind the properties of inequalities, such as the addition/subtraction property, multiplication/division property, and the transitive property. These properties allow us to manipulate the inequality without changing its solution set and help to simplify the problem and find the solution.
To solve inequalities, one must follow certain steps such as isolating the variable, applying the correct operations to both sides of the inequality, and determining the appropriate inequality symbol based on the direction of the inequality.
Types of Inequalities
Inequalities are mathematical expressions that compare two quantities and show their relationship. There are several different types of inequalities, each with its own set of rules and properties.
1. Linear Inequalities: Linear inequalities involve linear expressions, which are equations with variables raised to the first power only. These inequalities can be graphed on a number line and have a solution set that forms a shaded region.
2. Quadratic Inequalities: Quadratic inequalities involve quadratic expressions, which are equations with variables raised to the second power. These inequalities often have a curved graph and can have multiple solution sets or no solution.
3. Absolute Value Inequalities: Absolute value inequalities involve the absolute value function, which determines the distance between a number and zero. These inequalities often have two solution sets and the graph forms a V-shape.
4. Rational Inequalities: Rational inequalities involve rational expressions, which are fractions with variables in the numerator or denominator. These inequalities often have non-linear graphs and can have multiple solution sets or no solution.
5. Exponential Inequalities: Exponential inequalities involve exponential expressions, which are equations with variables raised to a constant exponent. These inequalities often have a curved graph and can have multiple solution sets.
Understanding the different types of inequalities is important for solving various mathematical problems and equations. By knowing the properties and rules of each type, you can confidently approach solving inequalities and determine their solutions.
Methods for solving inequalities
When solving inequalities, there are several methods that can be used to determine the solution set. One common method is graphing, where the inequality is represented on a number line or coordinate plane. This allows for a visual representation of the solution set and helps to identify the values that satisfy the inequality.
Another method is algebraic manipulation, which involves applying mathematical operations to both sides of the inequality in order to isolate the variable. This may include adding or subtracting terms, multiplying or dividing by constants or variables, or taking square roots. By performing the same operations on both sides, the inequality remains balanced and the solution set can be determined.
Additionally, inequalities can also be solved using interval notation. In this method, the solution set is represented by an interval or combination of intervals on the number line. The inequality symbol determines whether the interval is open or closed, and the endpoints of the interval represent the values that satisfy the inequality.
It is important to note that when solving inequalities, the solution set may be an infinite set of values, rather than a single solution. This is because the inequality represents a range of values that satisfy the given conditions.
In summary, when solving inequalities, graphing, algebraic manipulation, and interval notation are all useful methods for determining the solution set. Each method provides a different approach to visualizing or representing the values that satisfy the inequality, and the choice of method may vary depending on the specific problem or preference of the solver.
Common mistakes to avoid
When solving inequalities, it is important to be careful and avoid common mistakes that can lead to incorrect answers. Here are some common mistakes to watch out for:
- Forgetting to reverse the inequality sign when multiplying or dividing by a negative number. When you multiply or divide both sides of an inequality by a negative number, the direction of the inequality sign must be reversed. Failure to do so can result in an incorrect solution.
- Not combining like terms correctly. When simplifying an inequality, it is important to combine like terms correctly. Failure to do so can lead to errors in the final solution. Remember to add or subtract like terms before applying any operations.
- Ignoring the domain of the variable. When solving an inequality, it is important to consider the domain of the variable. The solution to an inequality may be valid only within a certain range of values. Ignoring the domain can lead to incorrect solutions.
- Not graphing the solution correctly. In some cases, it may be necessary to graph the solution to an inequality. Failing to accurately graph the solution can result in an incorrect representation of the solution set. Pay attention to the direction of the inequality and the shading of the graph.
- Using incorrect inequality rules. It is important to have a solid understanding of the rules for solving inequalities. Using incorrect rules or applying them improperly can lead to incorrect solutions. Make sure to review and fully understand the rules before attempting to solve any inequalities.
Avoiding these common mistakes can help ensure that your solutions to inequalities are accurate and correct.
Why practice solving inequalities?

Solving inequalities is an important skill to have in mathematics. It allows us to find the set of values that satisfy a given inequality and helps us understand the relationship between different variables. By practicing solving inequalities, we can improve our problem-solving abilities and develop critical thinking skills.
One of the main reasons for practicing solving inequalities is to be able to analyze real-life scenarios. Many real-world problems can be represented using mathematical inequalities. By being proficient in solving inequalities, we can effectively model and solve problems related to finance, economics, engineering, and many other fields.
Solving inequalities also plays a crucial role in understanding and graphing linear inequalities on a coordinate plane. By solving these equations, we can determine which side of the line represents the solutions. This knowledge is essential for interpreting graphs, understanding inequalities in two or more variables, and solving systems of inequalities.
Tips for preparing for the unit test
In order to prepare effectively for the Solving Inequalities unit test, it is important to review the key concepts and strategies covered in the unit. Here are some tips to help you succeed:
- Review the basic concepts: Make sure you understand the fundamental concepts of inequalities, such as the symbols used to represent inequalities (<, >, ≤, ≥) and how to read and interpret them.
- Practice solving inequalities: Work through a variety of practice problems to reinforce your understanding of how to solve inequalities. This will help you become familiar with different strategies and techniques.
- Understand the properties of inequalities: Familiarize yourself with properties such as the addition and multiplication properties of inequalities, which are used to manipulate and solve inequalities.
- Know how to graph inequalities: Learn how to graph linear inequalities on a number line and how to interpret the graphical representation of inequalities.
- Master word problems: Practice solving word problems that involve inequalities. Pay attention to the language used in the problem and identify the key information to set up and solve the inequality.
- Review your class notes and textbook: Go over your class notes and the relevant sections in your textbook to refresh your memory on the topics covered.
- Seek help if needed: If you are struggling with any concepts or solving certain types of inequalities, don’t hesitate to reach out for help. Ask your teacher or classmates for clarification or seek additional resources.
By following these tips and dedicating time to review and practice, you will be better prepared for the Solving Inequalities unit test and increase your chances of achieving success. Good luck!