Trigonometry is a branch of mathematics that deals with the relationships between the angles and sides of triangles. It is an essential skill for understanding and solving problems in fields such as engineering, physics, and navigation. To help students practice and assess their understanding of trigonometry concepts, teachers often provide worksheets with various problems to solve. These worksheets typically include a set of questions and exercises that cover topics such as trigonometric ratios, angles of elevation and depression, and trigonometric identities. After completing the worksheet, students can compare their answers with the trigonometry review worksheet answers to assess their performance and identify areas for improvement.
The trigonometry review worksheet answers provide students with a reference to check their work and ensure that they have correctly solved the problems. They can be used as a study guide to reinforce the concepts learned in class and serve as a valuable resource for exam preparation. By reviewing the answers, students can identify any misconceptions or errors they may have made and seek clarification from their teacher or peers.
In addition to providing answers, some trigonometry worksheets also include detailed explanations for each problem. These explanations can help students understand the step-by-step process of solving a particular trigonometry problem and reinforce their understanding of the underlying concepts. By reviewing the explanations, students can gain insight into different problem-solving strategies and develop a deeper understanding of the topic.
How to Use a Trigonometry Review Worksheet: Answers and Tips
Trigonometry can be a challenging subject for many students, but with the right tools and practice, it can become much easier to understand. One useful tool for reviewing and practicing trigonometry concepts is a trigonometry review worksheet. These worksheets typically include a series of problems that cover various topics in trigonometry, such as angles, trigonometric functions, and trigonometric identities.
When using a trigonometry review worksheet, it is important to approach it with a systematic and organized strategy. Here are some tips to help you make the most out of your review worksheet:
- Read the instructions carefully: Before you begin solving the problems on the worksheet, make sure to read the instructions carefully. This will help you understand what is expected from you and how to approach each problem.
- Review the relevant concepts: Before jumping into the problems, take some time to review the relevant trigonometry concepts. This will help refresh your memory and ensure that you have a solid understanding of the material.
- Work through each problem step by step: When solving the problems on the worksheet, take the time to work through each problem step by step. This will help you avoid mistakes and ensure that you fully understand the process.
- Check your answers: Once you have completed all the problems, it is important to check your answers. This will help you identify any mistakes and areas that you need to review further.
- Seek help if needed: If you are struggling with a particular problem or concept, don’t hesitate to seek help. Ask your teacher or a classmate for clarification, or consider using online resources or tutoring services.
A trigonometry review worksheet can be an effective tool for reinforcing your understanding of trigonometry concepts. By following these tips and approaching the worksheet with a focused mindset, you can make the most out of your review and improve your trigonometry skills.
Understand the Purpose of a Trigonometry Review Worksheet
In the field of mathematics, trigonometry is a crucial subject that deals with the relationships between the angles and sides of triangles. It plays a significant role in various real-life applications, such as engineering, navigation, and physics. To ensure a solid understanding of trigonometric concepts, students often engage in practice exercises and revision. One effective tool that educators utilize for this purpose is a trigonometry review worksheet.
A trigonometry review worksheet aims to consolidate the knowledge and skills acquired in the subject. It typically includes a range of questions that cover different aspects of trigonometry, such as finding angles and sides of triangles using trigonometric ratios, applying trigonometric identities, and solving trigonometric equations. The questions are designed to challenge students and reinforce their understanding of the concepts they have learned.
These review worksheets serve multiple purposes. Firstly, they help students identify areas of strength and weakness in their trigonometry knowledge. By attempting the various questions, students can gauge their level of understanding and identify specific topics or concepts that may require further review. This self-assessment allows students to focus their study efforts on the areas where they need improvement.
Secondly, trigonometry review worksheets provide an opportunity for students to practice applying the concepts they have learned. The questions are often carefully structured to test students’ problem-solving abilities and their ability to apply trigonometric principles in real-world scenarios. Through repeated practice, students can solidify their understanding and develop the necessary skills to tackle more complex trigonometry problems.
Overall, a trigonometry review worksheet serves as a valuable tool in the learning process. It helps students consolidate their knowledge, identify areas that require further review, and practice applying trigonometric concepts. By engaging with these worksheets, students can strengthen their understanding of trigonometry and build a solid foundation for future mathematical studies and real-life applications.
Review Key Concepts Covered in Trigonometry
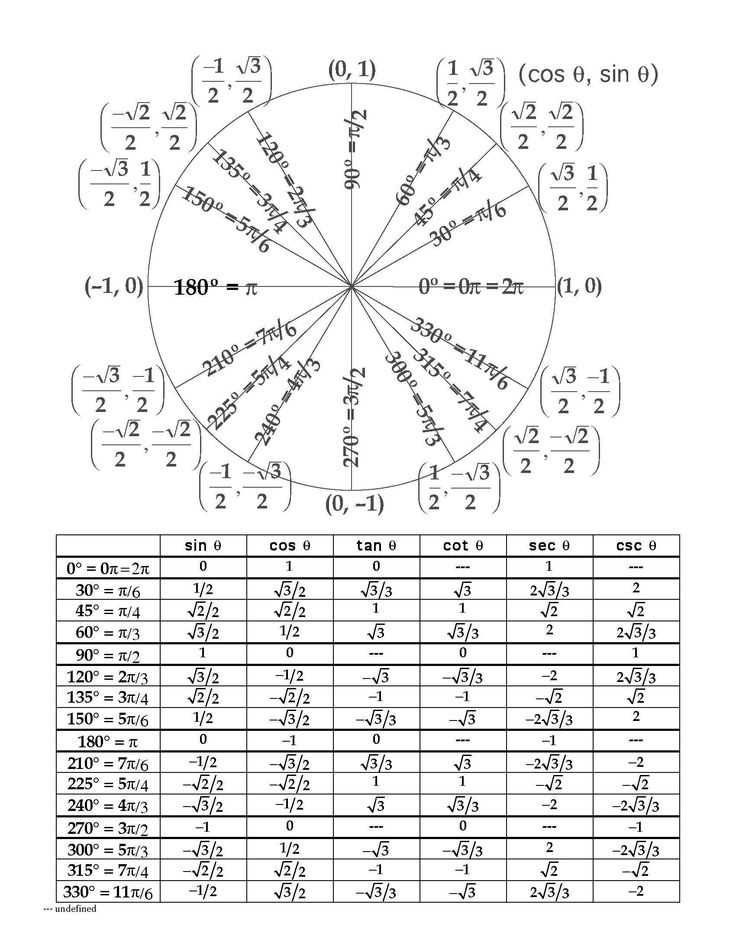
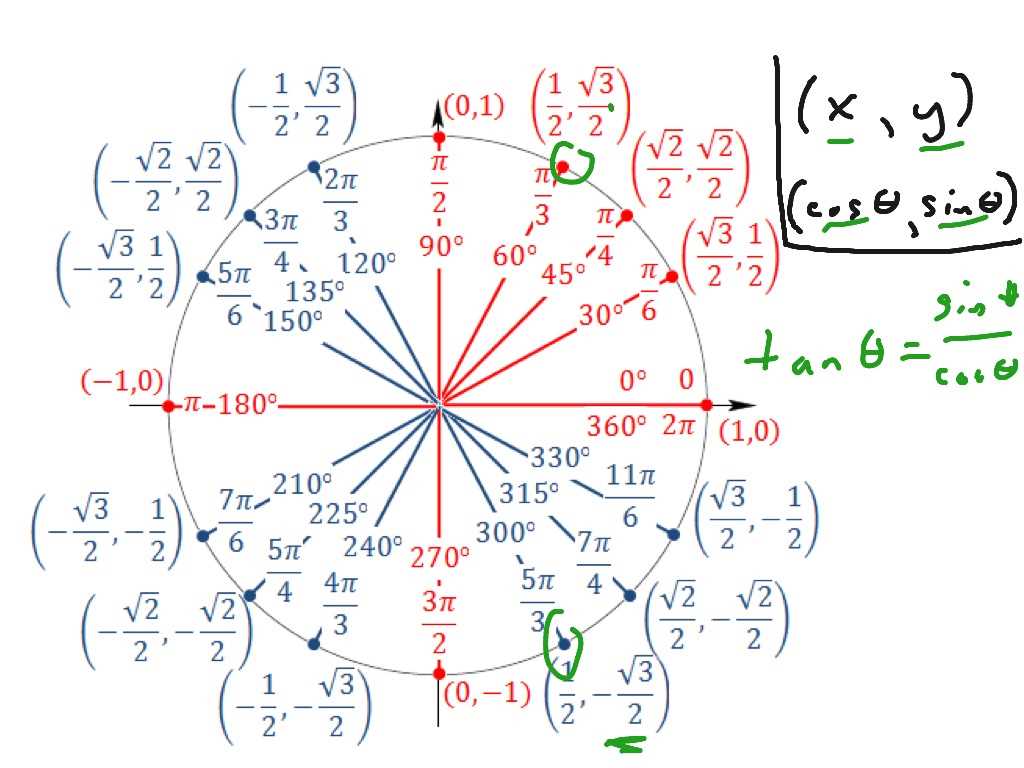
In trigonometry, we study the relationships between the sides and angles of triangles. One of the most fundamental concepts in trigonometry is the definition of the trigonometric functions: sine, cosine, and tangent. These functions relate the ratios of the lengths of the sides of a right triangle to the angles in the triangle.
Sine: The sine of an angle in a right triangle is defined as the ratio of the length of the side opposite the angle to the length of the hypotenuse. It is often represented as sin(A) or sinθ.
Cosine: The cosine of an angle in a right triangle is defined as the ratio of the length of the adjacent side to the length of the hypotenuse. It is often represented as cos(A) or cosθ.
Tangent: The tangent of an angle in a right triangle is defined as the ratio of the length of the opposite side to the length of the adjacent side. It is often represented as tan(A) or tanθ.
These trigonometric functions can be used to solve a variety of problems involving angles and lengths in triangles. For example, we can use the sine function to find the length of a side of a triangle when we know the measure of an angle and the length of another side.
Another key concept in trigonometry is the unit circle. The unit circle is a circle with a radius of 1, centered at the origin of a coordinate plane. By placing angles in standard position on the unit circle, we can define the trigonometric functions for any angle, not just those in right triangles.
In addition to the trigonometric functions, trigonometry also involves the study of trigonometric identities, which are equations involving the trigonometric functions that are true for all angles. These identities can be used to simplify trigonometric expressions or solve trigonometric equations.
Overall, a thorough understanding of these key concepts in trigonometry is essential for solving problems involving angles and lengths in triangles, as well as more advanced applications in fields such as physics and engineering.
Work through Sample Problems with Step-by-Step Answers
Trigonometry can be a challenging subject, but with practice and a clear understanding of the concepts, you can excel in this branch of mathematics. One effective way to reinforce your learning is by working through sample problems with step-by-step answers. This allows you to see the process of solving each problem and identify any mistakes or misunderstandings.
Start by selecting a trigonometry problem that aligns with the specific topic you are reviewing, such as solving for missing angles or sides in right triangles, using trigonometric identities, or applying trigonometric functions to real-life situations. Once you have chosen a problem, follow these steps:
- Understand the problem: Read the problem carefully and identify what information is given and what you need to find. This step is crucial in ensuring that you approach the problem correctly.
- Draw a diagram: Create a diagram that represents the given information, especially if the problem involves angles and sides of a triangle. This visual representation can help you better understand the problem and visualize the solution.
- Apply trigonometric concepts: Use the appropriate trigonometric concepts, such as sine, cosine, or tangent, to set up the necessary equations. Remember to use the relevant trigonometric ratios based on the information given in the problem.
- Solve the equations: Simplify and solve the equations to find the values of the missing angles or sides. Show all your steps clearly to ensure accuracy.
- Check your answer: Once you have found the solution, check your answer by plugging the values back into the original problem or using alternative methods to verify your results. This step is crucial in catching any calculation errors.
By working through sample problems with step-by-step answers, you not only reinforce your understanding of trigonometry but also develop problem-solving skills and gain confidence in tackling more complex problems. Make sure to practice regularly and seek clarification for any concepts or steps you find challenging. With persistence and dedication, you can master trigonometry and excel in your studies.
Get Explanation for Common Mistakes and Errors
A trigonometry review worksheet can be a useful tool for practicing and reinforcing concepts in trigonometry. However, it is common for students to make mistakes and errors while solving these worksheets. It is important to understand these mistakes and errors in order to improve understanding and performance in trigonometry.
One common mistake is the confusion between sine, cosine, and tangent ratios. Students often mix up the ratios and apply them incorrectly in specific contexts. For example, they may use the sine ratio when they should be using the cosine ratio. This confusion can lead to incorrect calculations and answers. To avoid this mistake, it is important to review the definitions and applications of each trigonometric ratio.
Another mistake is the incorrect use of the Pythagorean theorem. Students may forget to use the theorem or apply it incorrectly when solving trigonometric problems. This can result in incorrect lengths or measurements. To avoid this mistake, it is important to carefully analyze the problem and identify whether the Pythagorean theorem can be applied.
Additionally, students may make errors while solving trigonometric equations or applying trigonometric identities. They may skip steps or make calculations errors, leading to incorrect solutions. To avoid these errors, it is important to double-check calculations and show all steps in the solution process. It is also helpful to practice solving various types of trigonometric equations and familiarize oneself with common trigonometric identities.
Overall, getting an explanation for common mistakes and errors in trigonometry can greatly improve understanding and performance. By understanding these mistakes and actively working to avoid them, students can become more proficient in trigonometry and achieve better results in their studies. Practice, review, and seeking clarification or guidance when needed are essential steps in mastering trigonometry.
Check Your Solutions for Accuracy
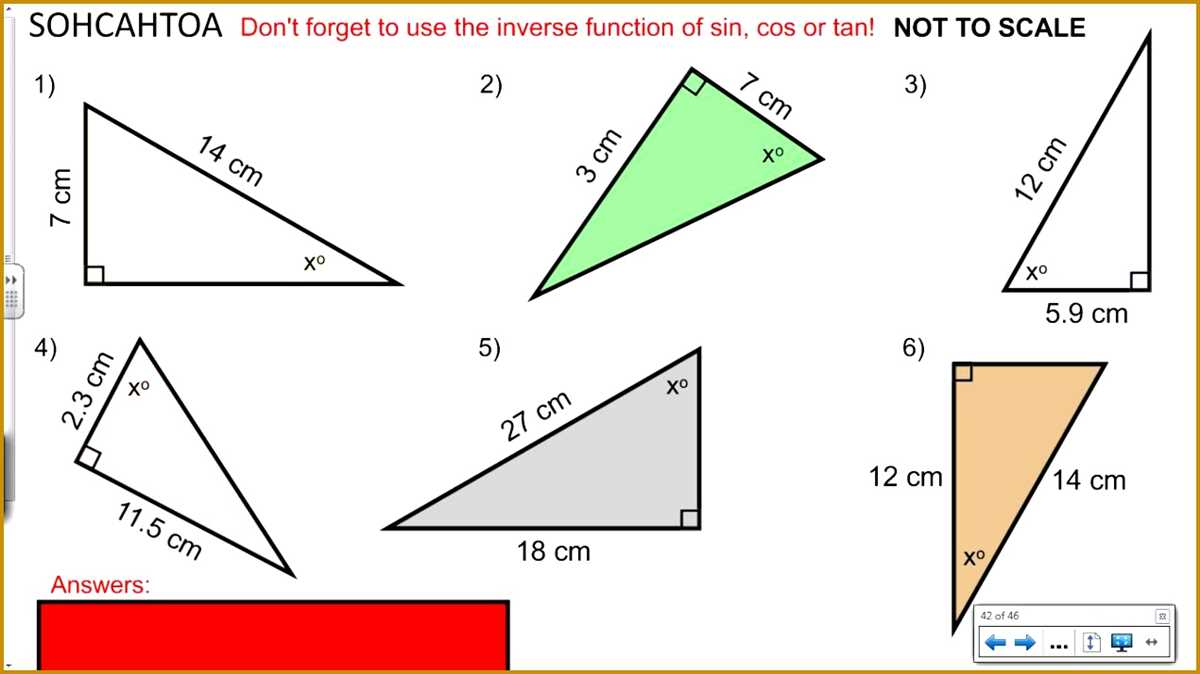
After completing a trigonometry review worksheet, it is important to check your solutions for accuracy. This ensures that you have correctly solved the problems and can have confidence in your understanding of the material.
One way to check your solutions is to substitute them back into the original equation or problem and see if they satisfy the given conditions. This is especially important when solving trigonometric equations or expressions. For example, if you have solved for the value of a certain angle, you can plug that value back into the equation and see if both sides are equal.
If you are solving for an unknown side length or angle measurement in a right triangle, you can also use the Pythagorean theorem or the trigonometric ratios to check your solution. For example, if you have solved for the length of a side using the sine ratio, you can use the sine ratio again to see if the lengths of the other sides are consistent with your solution.
Another way to check your solutions is to use a graphing calculator or software to plot the graph of the trigonometric function or equation. This can help you visualize the solution and verify that it matches the graph. You can compare the x-values of the graph with the solutions you obtained to ensure they are correct.
It is also helpful to double-check your calculations and algebraic steps to make sure you have not made any errors along the way. Take the time to review your work, paying attention to signs, units, and any simplifications you made. This can help catch any mistakes before they lead to incorrect solutions.
In summary, checking your solutions for accuracy is an important step in a trigonometry review. By substituting solutions back into the original equation, using the Pythagorean theorem or trigonometric ratios, using a graphing calculator, and double-checking your calculations, you can ensure that your solutions are correct and build confidence in your knowledge of trigonometry.
Tips for Using a Trigonometry Review Worksheet Effectively
Trigonometry can be a challenging subject, but with the right resources and study materials, you can improve your understanding and mastery of the concepts. One such resource is a trigonometry review worksheet. These worksheets are designed to help you practice and reinforce your knowledge of trigonometry principles and formulas. To make the most of your review worksheet, here are some tips to keep in mind:
- Read the instructions carefully: Before diving into the problems on the worksheet, take the time to thoroughly read the instructions. Make sure you understand what is being asked of you and what format the answers should be in.
- Start with the basics: Trigonometry builds upon foundational concepts, so it’s important to have a solid understanding of the basics. If you’re struggling with a particular topic, take the time to revisit the fundamentals before attempting more advanced problems.
- Work through problems step by step: Trigonometry problems often involve multiple steps, so it’s important to break them down and tackle each step individually. This will help you avoid mistakes and ensure that you’re on the right track.
- Seek help when needed: If you’re stuck on a problem or can’t seem to understand a concept, don’t hesitate to ask for help. Reach out to your teacher, classmates, or online resources for clarification and guidance.
- Review your answers: After completing the worksheet, go back and review your answers. Look for any errors or areas where you could improve. Understanding your mistakes will help you identify areas that need further study and practice.
By following these tips, you can make the most of your trigonometry review worksheet and enhance your understanding of the subject. Remember to practice regularly and seek out additional resources as needed. With dedication and persistence, you can improve your trigonometry skills and succeed in your studies.