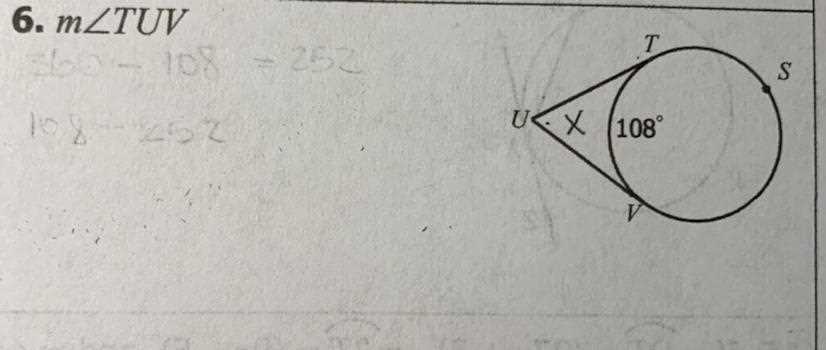
Welcome to the answer key for Unit 10 Circles Homework 3 on Arc Lengths! In this article, we will go over the answers to the homework questions related to finding arc lengths in circles. Arc lengths are an important concept in geometry, as they help us understand the distance along a curved line on a circle.
In this homework, you were given various circles and asked to find the length of the arcs. To find the arc length, we use a formula that involves the central angle and the radius of the circle. This formula is derived from the fact that the circumference of a circle is directly proportional to the central angle:
Arc Length = (Central Angle / 360) x (2πr)
Using this formula, we can calculate the arc length for any given circle. The central angle is measured in degrees, and the radius of the circle is measured in units. By plugging in the values for the central angle and the radius into the formula, we can easily find the length of the arc.
In this answer key, we will provide step-by-step solutions to each of the homework questions, along with explanations for each step. By going through these solutions, you will gain a better understanding of how to find arc lengths in circles and improve your overall knowledge of geometry. Let’s get started!
Explanation of Arc Lengths
In geometry, an arc is a portion of the circumference of a circle. The length of an arc is defined as the distance along the circle’s edge between two points on the circumference. The concept of arc length is essential in various applications, such as calculating the distance traveled along a curved path or determining the length of specific portions of a circular object.
To calculate the length of an arc, one must consider two factors: the measure of the central angle that the arc subtends and the radius of the circle. The formula to find the arc length is given by:arc length = (central angle/360) x 2πr
Here, the central angle is measured in degrees and the radius (r) is the distance from the center of the circle to any point on its circumference. The expression (central angle/360) calculates the fraction of the entire circle’s circumference that the arc represents, and multiplying it by 2πr gives the actual length of the arc.
An important property of arcs is that they can be proportional to the central angle they subtend. In other words, if two arcs subtend two central angles in a circle, then the ratio of their lengths is equal to the ratio of their respective central angles. This property allows for convenient comparisons and calculations involving arcs.
Understanding arc lengths is crucial in various fields, including engineering, architecture, and physics. It allows for precise measurements and calculations involving curved objects and paths, providing valuable information for design, analysis, and problem-solving.
Overview of homework 3 in Unit 10 circles
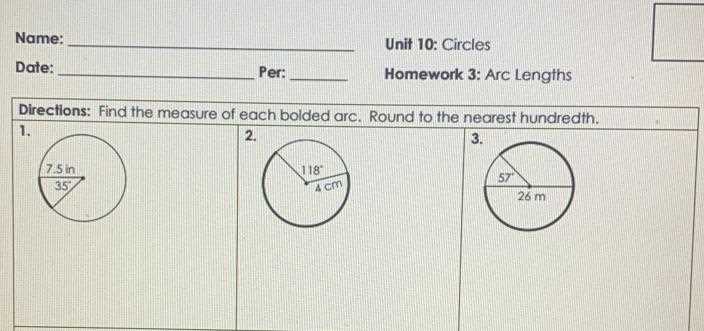
In homework 3 of Unit 10 in circles, students will be working with the concept of arc lengths. Arc length is the measure of the distance along the curved part of a circle, and it is given in terms of the fraction of the circumference it represents. To find the arc length, students will need to know the measure of the central angle that subtends the arc, as well as the circumference of the circle.
The homework assignment will provide students with various problems involving arc lengths. These problems will require them to apply the formula for arc length, which states that the arc length is equal to the circumference of the circle multiplied by the fraction of the circle represented by the central angle. Students will need to manipulate the given information to find either the measure of the central angle or the arc length itself.
The homework will also include word problems that require students to interpret and solve real-life scenarios involving arc lengths. These problems will help students develop their problem-solving skills and apply their understanding of arc lengths in practical situations. Students will need to read the problem carefully, identify the relevant information, and apply the appropriate formula to find the solution.
In summary, homework 3 in Unit 10 circles focuses on arc lengths. Students will practice using the formula for arc length and apply their understanding in both numerical and real-life situations. This assignment will help them reinforce their knowledge of circles and develop their problem-solving skills.
Answer key for Unit 10 circles homework 3
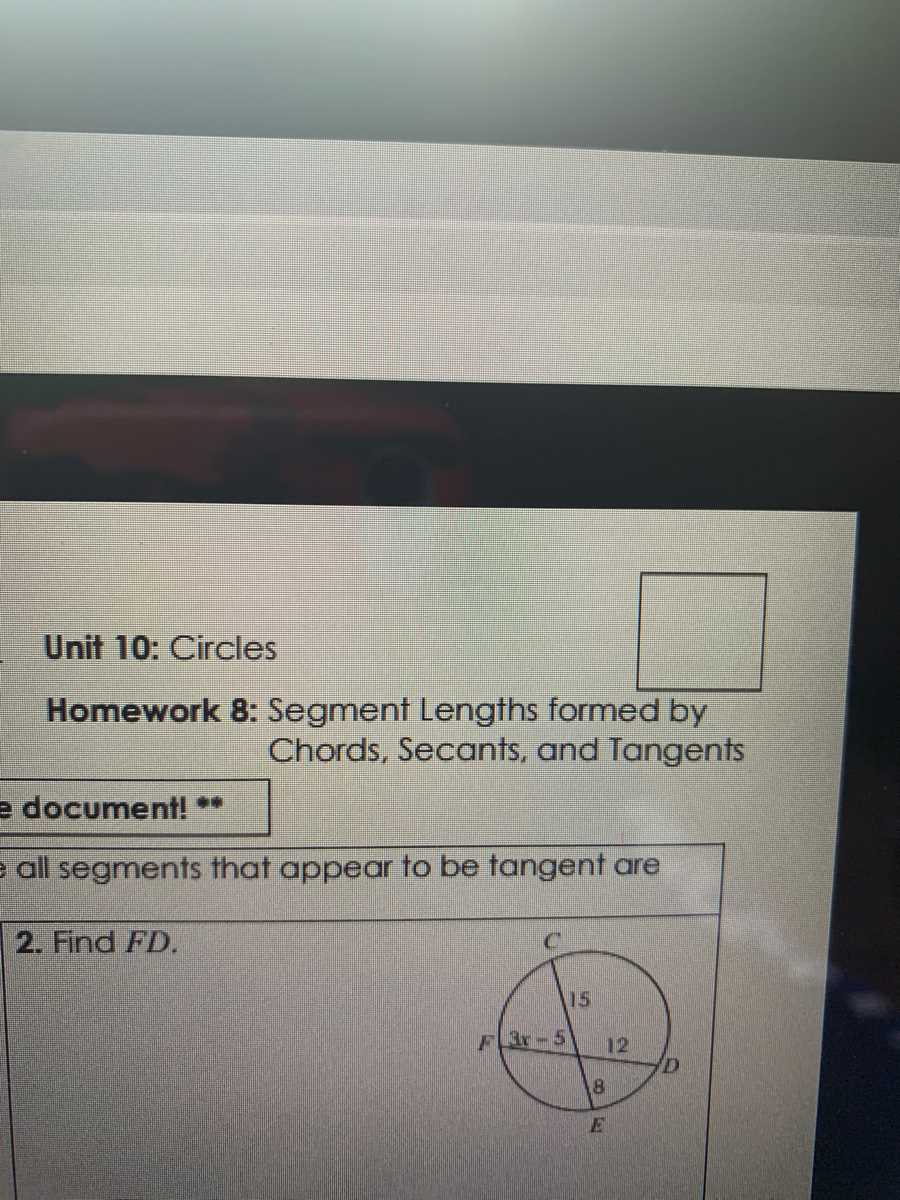
Here is the answer key for Unit 10 circles homework 3:
- Question 1: The arc length of a circle is calculated using the formula: $arc length = dfrac{angle measure}{360} times 2 pi r$, where $r$ is the radius of the circle. Substitute the given values into the formula and calculate the arc length.
- Question 2: The length of an arc is given as 8 cm and the radius of the circle is 4 cm. To find the angle measure, use the formula: $angle measure = dfrac{arc length}{2 pi r} times 360$. Substitute the given values and calculate the angle measure.
- Question 3: The area of a sector of a circle is calculated using the formula: $area = dfrac{angle measure}{360} times pi r^2$. Substitute the given values into the formula and calculate the area of the sector.
- Question 4: The area of a sector of a circle is 6 square meters and the radius of the circle is 3 meters. To find the angle measure, use the formula: $angle measure = dfrac{area times 360}{pi r^2}$. Substitute the given values and calculate the angle measure.
- Question 5: To find the circumference of a circle, use the formula: $circumference = 2 pi r$, where $r$ is the radius of the circle. Substitute the given values and calculate the circumference.
These are the answers for Unit 10 circles homework 3. Make sure to double-check your work and understand the formulas used to solve the problems.
Common Mistakes to Avoid in Unit 10 Circles Homework 3
In Unit 10 Circles Homework 3, it is important to pay attention to detail and avoid common mistakes that can lead to incorrect answers. Here are some common mistakes to avoid:
1. Forgetting to convert units
When dealing with arc lengths, it is important to make sure that you are using the correct units. If the question asks for the arc length in inches, make sure your answer is in inches. Forgetting to convert units can lead to incorrect answers.
2. Misinterpreting the question
Always take the time to carefully read and understand the question. Misinterpreting the question can lead to incorrect calculations and answers. Pay attention to keywords such as “arc length,” “central angle,” and “radius.”
3. Incorrectly using the formula
The formula for calculating arc length is L = 2πr(θ/360), where L is the arc length, r is the radius, and θ is the central angle. Make sure you are using the formula correctly and plugging in the values in the right places.
4. Rounding errors
When performing calculations, it is important to round to the appropriate number of decimal places or significant figures as indicated in the question. Rounding errors can lead to slight discrepancies in the final answer.
5. Forgetting to consider the full circle
It is important to remember that a full circle has 360 degrees or 2π radians. When dealing with arcs that are not a complete circle, make sure to adjust the formula and calculations accordingly.
By being mindful of these common mistakes and practicing careful attention to detail, you can avoid errors and successfully complete Unit 10 Circles Homework 3.