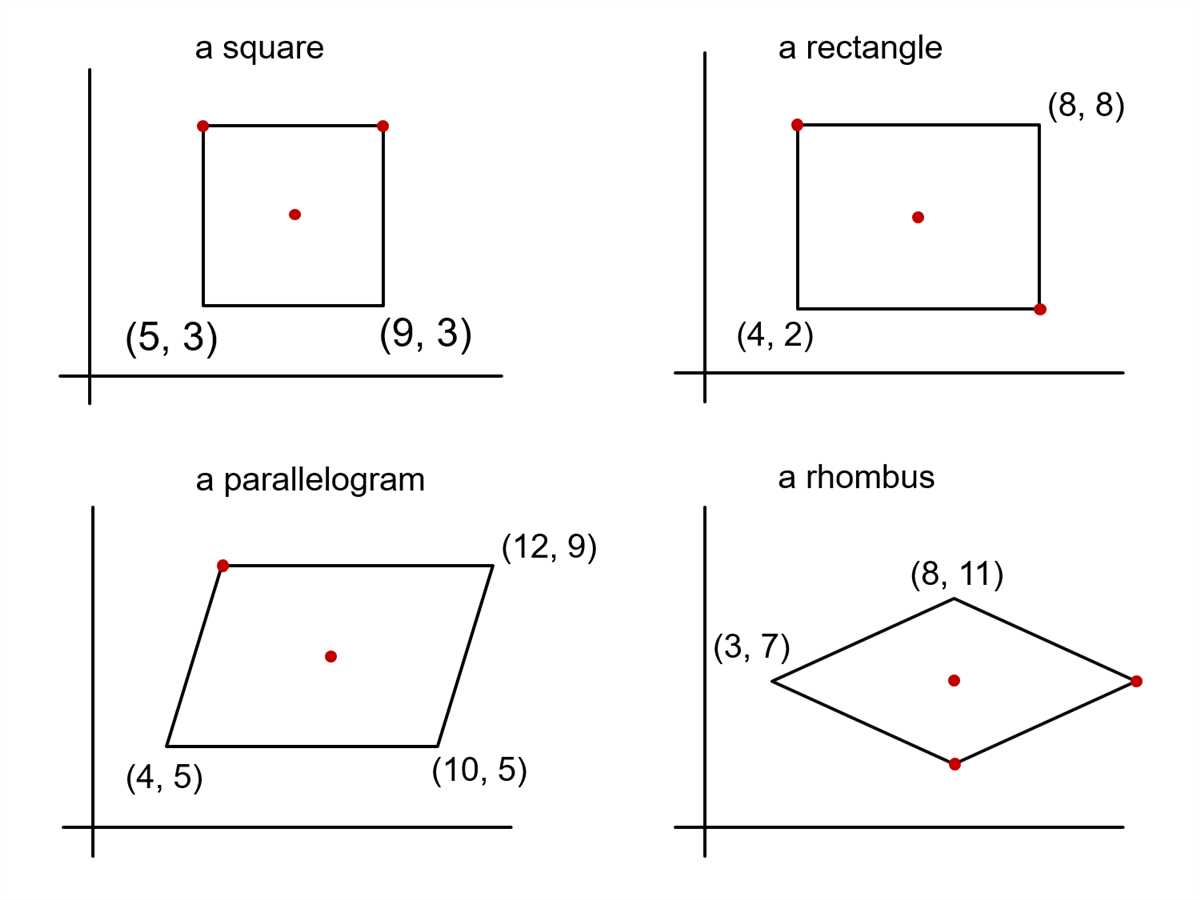
Parallelograms are an essential geometric shape that often appears in various mathematical problems and real-life situations. They possess unique properties and characteristics that distinguish them from other quadrilaterals. To fully comprehend and master the concept of parallelograms, it is crucial to work on practice worksheets that provide exercises to assess and strengthen understanding.
The 6.2 Parallelograms Worksheet is an excellent resource for students, teachers, and enthusiasts seeking to enhance their knowledge and skills in dealing with parallelograms. This worksheet consists of a series of questions designed to test comprehension and ability in identifying, classifying, and calculating various aspects of parallelograms.
The worksheet provides answers to each question, which is invaluable for individuals looking to verify their solutions or seek guidance. It allows for self-assessment and helps in identifying areas of improvement. With these answers readily available, individuals can better understand the logic and techniques required to solve parallelogram-related problems.
By utilizing the 6.2 Parallelograms Worksheet and its accompanying answers, individuals can not only solidify their understanding of parallelograms but also refine their problem-solving skills. Working through the questions and checking the answers will lead to increased confidence and proficiency in handling parallelogram-centric mathematical challenges.
Parallelograms Worksheet Answers
A parallelogram is a quadrilateral with opposite sides that are parallel and equal in length. It also has opposite angles that are congruent. To understand the properties of parallelograms better, a worksheet is often used to practice and test one’s knowledge.
In a parallelograms worksheet, students are provided with various problems and questions related to parallelograms. These worksheets can cover topics such as finding missing angles or sides of parallelograms, identifying the properties of parallelograms, and solving word problems involving parallelograms.
Sample questions and answers on a parallelograms worksheet:
- Find the value of x in the parallelogram below:
- Given that ABCD is a parallelogram and angle A = 70°, find angle B.
- Find the perimeter of a parallelogram with sides of length 8 cm and 12 cm.
|
|
Answer: x = 40°
Answer: Angle B = 110° (opposite angles in a parallelogram are congruent).
Answer: The perimeter of the parallelogram is 40 cm (2 * (8 cm + 12 cm)).
Parallelograms worksheets are essential tools for practicing and reinforcing the concepts and properties of parallelograms. They enable students to apply their knowledge and skills in solving various types of problems involving parallelograms.
Understanding Parallelograms
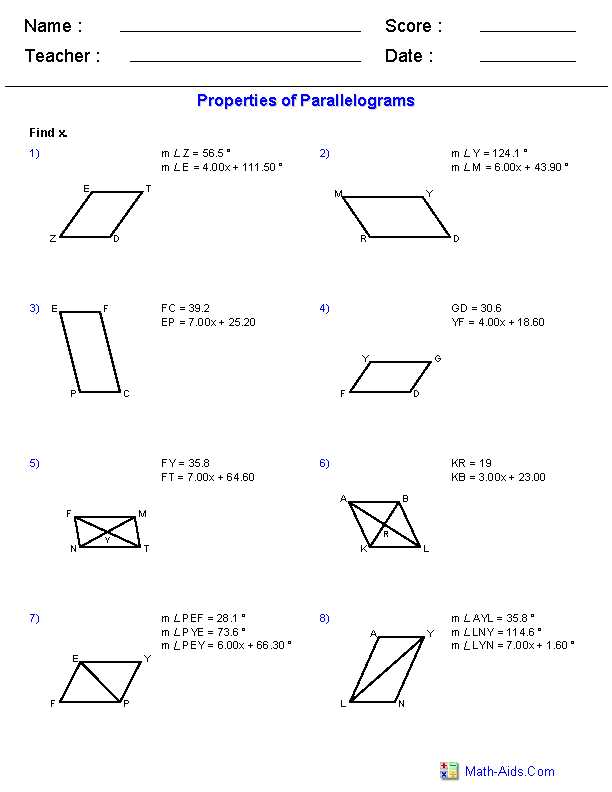
What is a parallelogram?
A parallelogram is a special type of quadrilateral where opposite sides are parallel and equal in length. It can be thought of as a “slanted” rectangle or a diamond shape. The properties of a parallelogram make it an important figure in geometry, as it exhibits unique characteristics that distinguish it from other polygons.
Properties of parallelograms:
- Opposite sides are parallel: This means that if you extend the sides of a parallelogram, they will never intersect.
- Opposite sides are equal: The length of the opposite sides of a parallelogram are always equal.
- Opposite angles are equal: The measure of the opposite angles in a parallelogram are always equal.
- Consecutive angles are supplementary: The sum of the consecutive angles in a parallelogram is always 180 degrees.
- Diagonals bisect each other: The diagonals of a parallelogram bisect each other, meaning they divide each other into two equal parts.
Applications of parallelograms:
Parallelograms can be found in various real-world scenarios. For example, the shape of a playing card is a parallelogram. The shape of a sail on a sailboat is also a parallelogram. In construction, parallelograms are commonly used for creating trusses and supporting structures. Understanding the properties and characteristics of parallelograms can help in solving problems and designing structures that require stability and balance.
Properties of Parallelograms
A parallelogram is a quadrilateral with two pairs of parallel sides. This means that opposite sides of a parallelogram are equal in length and parallel to each other. Additionally, opposite angles in a parallelogram are equal in measure.
One important property of parallelograms is that the opposite sides are congruent. This means that if one pair of opposite sides in a parallelogram is equal in length, then the other pair of opposite sides must also be equal in length. This can be seen in the diagram below:
| Property | Diagram |
|---|---|
| Opposite Sides are Equal |
|
Another property of parallelograms is that the opposite angles are congruent. This means that if one pair of opposite angles in a parallelogram is equal in measure, then the other pair of opposite angles must also be equal in measure. This can be seen in the diagram below:
| Property | Diagram |
|---|---|
| Opposite Angles are Equal |
|
In addition to these properties, parallelograms also have other properties such as the diagonals bisecting each other and the sum of the interior angles being equal to 360 degrees. These properties make parallelograms useful in geometry and provide a basis for solving problems involving their measurements and relationships.
Calculating Area of Parallelograms
When it comes to finding the area of parallelograms, there is a simple formula that can be used. The area of a parallelogram is equal to the base multiplied by the height. The base of a parallelogram is any of its sides, while the height is the perpendicular distance between the base and the opposite side.
In order to find the area of a parallelogram, it is important to first measure the length of the base and the height. The base can be any of the sides, so it is essential to identify which side will be used as the base. The height is the perpendicular distance between the chosen base and the opposite side. Once the measurements are obtained, the area can be calculated by multiplying the base and the height.
For example, let’s consider a parallelogram with a base length of 8 units and a height of 5 units. The area of this parallelogram can be found by multiplying 8 units (the base) by 5 units (the height), resulting in an area of 40 square units. It is important to note that the units used for measurements should be consistent throughout the calculation.
Calculating the area of parallelograms is a fundamental concept in geometry. It allows us to determine the amount of space inside these two-dimensional shapes. Whether for practical purposes or academic exercises, understanding the formula and applying it correctly is essential in solving problems involving parallelograms.
Using Diagonals in Parallelograms
A diagonal is a line segment that connects two nonadjacent vertices in a polygon. In the case of parallelograms, the diagonals are particularly useful in understanding the properties and relationships within the shape. Let’s explore the different ways diagonals can be used in parallelograms:
1. Bisecting each other: The diagonals of a parallelogram bisect each other. This means that the point where the diagonals intersect divides each diagonal into two equal segments. This property can be helpful in finding the measurements of different parts of the parallelogram.
2. Creating congruent triangles: The diagonals of a parallelogram divide it into four congruent triangles. This means that the two triangles formed by one diagonal are congruent to the two triangles formed by the other diagonal. This property can be useful in proving the congruence of different parts of the parallelogram.
3. Finding the area: The diagonals of a parallelogram can also be used to find the area of the shape. The area of a parallelogram can be calculated by multiplying the length of one diagonal by the length of the perpendicular dropped from a vertex to the opposite diagonal. This property can be helpful in solving various problems related to finding the area of a parallelogram.
Overall, the diagonals of a parallelogram are important in understanding its properties and relationships. They can be used to bisect each other, create congruent triangles, and find the area of the shape. By understanding and utilizing these properties, we can solve various problems related to parallelograms and further explore the geometry of these fascinating shapes.
Application Problems
In this section, we will solve application problems that involve parallelograms. These problems require us to use the properties and formulas related to parallelograms in order to find missing information or solve real-life situations.
Problem 1: A field in the shape of a parallelogram has a base of 30 meters and a corresponding height of 15 meters. Find the area of the field.
Solution: To find the area of the parallelogram, we can use the formula: Area = base × height. Plugging in the given values, we have: Area = 30 meters × 15 meters = 450 square meters. Therefore, the area of the field is 450 square meters.
Problem 2: The lengths of the sides of a parallelogram are in the ratio 4:5:6:7. Find the length of the shortest side if the longest side measures 28 centimeters.
Solution: Let’s denote the lengths of the sides as 4x, 5x, 6x, and 7x, where x is a common factor. From the given information, we know that 7x = 28 centimeters. Solving for x, we find that x = 4 centimeters. Therefore, the length of the shortest side is 4x = 4 centimeters × 4 = 16 centimeters.
These examples demonstrate how the properties of parallelograms can be applied to solve different types of problems. By understanding the formulas and relationships involved, we can find missing information and solve real-life scenarios involving parallelograms.
Practice Questions and Answers
Here are some practice questions and their corresponding answers to help you solidify your understanding of parallelograms:
1. What are the properties of a parallelogram?
- Opposite sides are parallel.
- Opposite sides are congruent.
- Opposite angles are congruent.
- Consecutive angles are supplementary.
2. Is a square a parallelogram?
Yes, a square is a special type of parallelogram because it has all the properties of a parallelogram, as well as additional properties such as all sides being congruent and all angles being right angles.
3. Find the missing measures in the parallelogram:
| Side | Length | Angle |
|---|---|---|
| AB | 5 cm | 30° |
| BC | ? | 120° |
| CD | 8 cm | ? |
| DA | ? | 60° |
Using the properties of a parallelogram, we can determine the missing measures as follows:
- BC = AB = 5 cm (opposite sides are congruent)
- Angle DCD = 180° – 120° = 60° (consecutive angles are supplementary)
- DA = BC = 5 cm (opposite sides are congruent)
4. Can a parallelogram have exactly one pair of congruent sides?
No, in a parallelogram, opposite sides must be congruent. Therefore, a parallelogram cannot have exactly one pair of congruent sides. If one pair of sides is congruent, the opposite pair of sides must also be congruent.
5. If one angle of a parallelogram measures 75°, what is the measure of its opposite angle?
Since opposite angles in a parallelogram are congruent, the measure of the opposite angle is also 75°.
In conclusion, parallelograms have several defining properties, including parallel sides, congruent opposite sides, congruent opposite angles, and supplementary consecutive angles. Squares are a special type of parallelogram with additional properties. Additionally, the practice questions and answers provided here can help reinforce your understanding of parallelograms.
