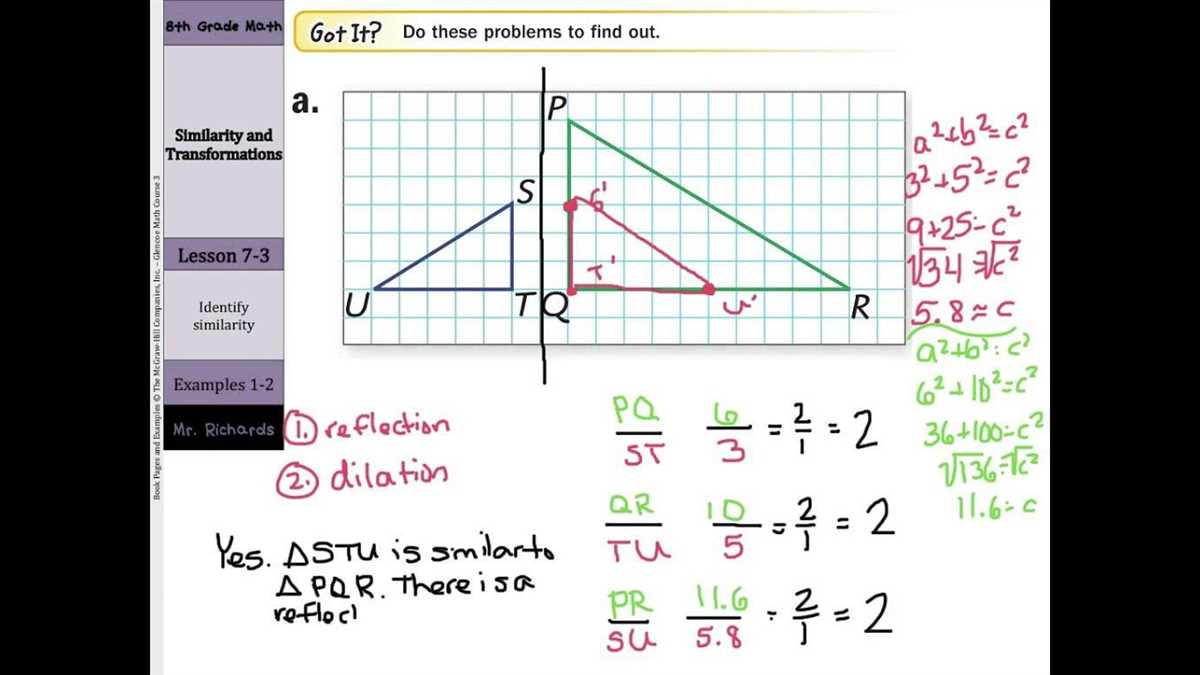
Understanding and applying similarity transformations is an essential skill in geometry, as it allows us to analyze and compare shapes in a meaningful and quantitative way. Whether it’s resizing an object, rotating it, or reflecting it, transformations help us explore the relationship between different figures and the properties that they share.
In this article, we will provide an answer key to some common questions and problems related to similarity and transformations. This answer key will serve as a guide for students and educators, helping them check their work, verify their solutions, and deepen their understanding of the topic.
The answer key will cover a range of topics, including determining if two figures are similar, finding the scale factor between them, identifying corresponding angles and sides, performing different types of transformations, and applying similarity to solve real-world problems. Each answer will be explained step by step, providing a clear and concise solution that will help clarify any confusion and build confidence in the subject matter.
What is Similarity?
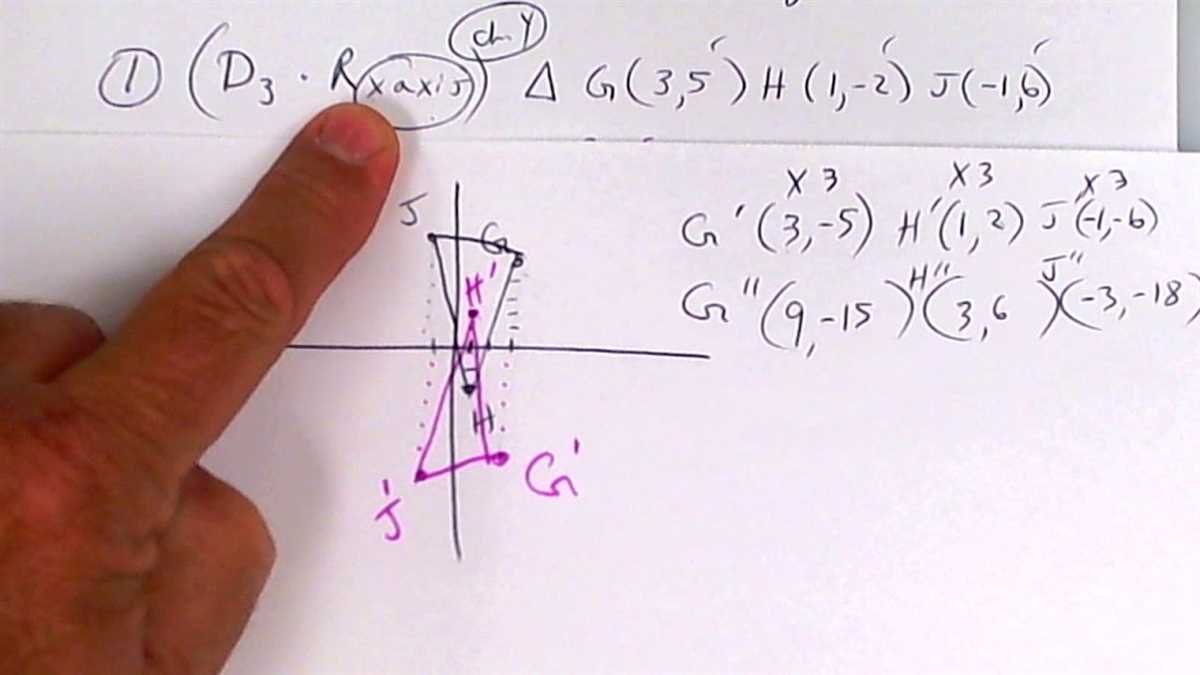
Similarity is a concept in geometry that refers to the relationship between two objects or figures that have the same shape but may differ in size. When objects or figures are similar, their corresponding angles are equal, and their corresponding sides are proportional. This means that if you were to enlarge or shrink one object, it would still have the same shape as the other object, just in a different size.
In order to determine if two objects are similar, we can use various methods such as the angle-angle similarity theorem or the side-angle-side similarity theorem. These theorems allow us to compare the angles and sides of two objects and determine if they are proportional and equal, respectively. Additionally, we can also use transformational methods such as translations, rotations, and reflections to determine if two objects are similar by comparing their corresponding vertices and lines of symmetry.
Similarity is an important concept in geometry as it allows us to study and analyze shapes and figures in a more general sense, without being limited to specific sizes or dimensions. It helps us understand the relationships between different objects and gives us the ability to create scale models or designs that preserve the shape of the original object or figure.
Understanding Similarity through Transformations
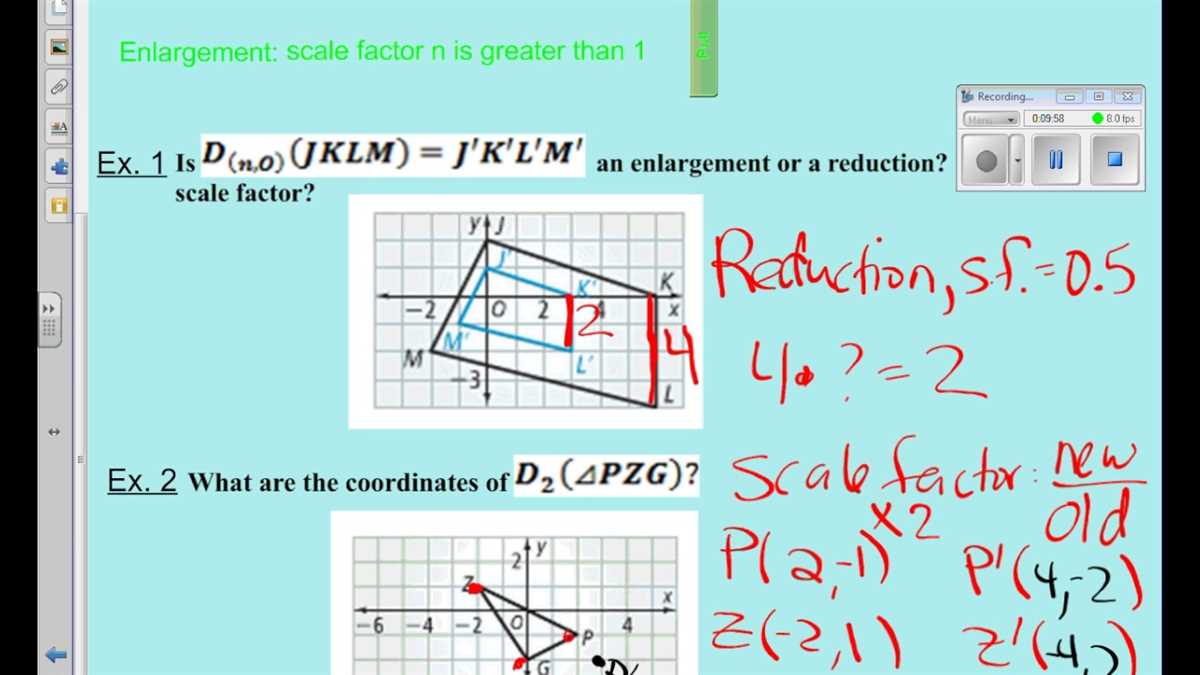
In the study of geometry, understanding similarity is crucial for analyzing and comparing different shapes and figures. One effective way to understand similarity is through transformations. Transformations are changes in position, size, or orientation of a shape or figure. By applying various transformations, such as translations, rotations, and reflections, we can explore the relationship between similar figures.
Translations: A translation is a transformation that moves every point of a shape or figure the same distance in the same direction. By applying a translation to a shape, we can observe how its size and orientation remain unchanged, indicating similarity. For example, if we translate a triangle, all its angles and side lengths will stay the same, showing that the two triangles are similar.
Rotations: A rotation is a transformation that turns a shape or figure around a fixed point. By rotating a shape, we can understand if it maintains its similarity with the original shape. If the angles and side lengths of a shape remain the same after a rotation, it indicates that the figures are similar.
Reflections: A reflection is a transformation that flips a shape or figure across a line, known as the line of reflection. When observing a shape or figure after a reflection, we can analyze if it maintains its similarity. If the angles and side lengths remain unchanged, it implies similarity between the original and reflected figures.
To summarize, understanding similarity is essential in geometry, and transformations provide a powerful tool for analyzing it. Whether through translations, rotations, or reflections, applying these transformations allows us to observe the relationship and similarity between different shapes and figures.
Exploring Similarity using Coordinate Geometry
In mathematics, similarity is a key concept that allows us to compare and analyze different geometric figures. One method to explore similarity is through the use of coordinate geometry. By assigning coordinates to the vertices of geometric figures, we can calculate the distances between points and analyze the ratios of these distances.
Coordinate geometry provides a precise and systematic way to determine if two figures are similar. To demonstrate this, let’s consider two triangles, Triangle ABC and Triangle XYZ. By assigning coordinates to their respective vertices, we can analyze the lengths of the sides and compare the ratios. If the ratios of corresponding side lengths are equal, then the triangles are considered similar.
Using the distance formula, we can calculate the lengths of the sides of the triangles. For example, the distance between points A(x1, y1) and B(x2, y2) can be found using the equation: √[(x2 – x1)² + (y2 – y1)²]. By calculating the lengths of the sides of Triangle ABC and Triangle XYZ, we can compare the ratios and determine if the two triangles are similar.
Understanding similarity using coordinate geometry enables us to not only compare and analyze geometric figures, but also to make predictions and solve real-world problems. For example, we can use similarity to determine the height of a flagpole, the width of a river, or the distance between two cities. By applying the principles of similarity and utilizing coordinate geometry, we can explore the world around us in a whole new way.
Solving Similarity Problems

When it comes to solving similarity problems, it is important to understand the concept of similarity and the different transformations that can be applied. Similarity refers to the geometric property of two figures having the same shape, but not necessarily the same size. This means that corresponding angles are congruent, and corresponding sides are proportional. Solving similarity problems involves determining the relationship between the corresponding sides and angles of two similar figures.
One method for solving similarity problems is using the scale factor. The scale factor is the ratio of the lengths of corresponding sides of two similar figures. By knowing the scale factor, you can determine the lengths of unknown sides by multiplying the known side lengths by the scale factor. Similarly, you can find the measures of unknown angles by multiplying the known angle measures by the scale factor.
Another approach to solving similarity problems is using proportions. Proportions involve setting up an equation where the ratio of corresponding sides is equal to the scale factor. By cross-multiplying and solving for the unknown variable, you can determine the length of the unknown side. Proportions can also be used to find the measure of an unknown angle by setting up an equation with the ratio of corresponding angle measures.
In some cases, solving similarity problems may require applying various transformations, such as translations, rotations, reflections, or dilations. These transformations can help determine the relationship between two similar figures. For example, by applying a translation or rotation, you can determine if two figures are congruent or similar. Dilations, on the other hand, can be used to create similar figures by changing the size of the original figure while keeping the shape intact.
In conclusion, solving similarity problems involves understanding the concept of similarity, using scale factors and proportions to determine the relationship between corresponding sides and angles, and applying various transformations as needed. By employing these strategies, you can successfully solve similarity problems and analyze the geometric properties of similar figures.
Using Proportions to Solve Similarity Problems
Solving similarity problems often requires the use of proportions. Proportions are ratios that are equal to each other. When dealing with similar figures, the corresponding side lengths are proportional. This means that the ratio of any two corresponding side lengths in the two figures will be the same.
Proportions can be used to find missing side lengths in similar figures. For example, if we have two similar triangles and we know the length of one side of the smaller triangle and the corresponding length of the larger triangle, we can set up a proportion to find the length of the missing side. We would write the proportion as:
Length of side in smaller triangle / Length of corresponding side in larger triangle = Length of missing side in smaller triangle / Length of corresponding side in larger triangle
Once we have set up the proportion, we can cross-multiply and solve for the missing side length. This method can be used to find missing side lengths in any similar figures, not just triangles. It is an essential tool for solving problems involving similarity.
In addition to finding missing side lengths, proportions can also be used to compare the areas of similar figures. Since the ratio of corresponding side lengths is the same, the ratio of the areas of the similar figures will be the square of the ratio of the side lengths. This can be a useful tool when comparing the sizes of different objects or solving problems involving scaling.
In conclusion, proportions are a powerful tool for solving similarity problems. They can be used to find missing side lengths and compare areas of similar figures. Understanding how to set up and solve proportions is essential for success in working with similarity.
Applying Similarity in Real-life Situations
In this article, we have explored the concept of similarity and how it can be applied in various real-life situations. Similarity plays a crucial role in many fields, including mathematics, physics, biology, and engineering. By understanding and utilizing the principles of similarity, we can solve problems and make predictions in these fields.
One real-life situation where similarity is applied is in map-making. Maps represent a scaled-down version of a larger geographical area. The scale of a map is determined by the relationship between the distances on the map and the corresponding distances on the ground. By using similar triangles, cartographers can accurately represent the real-world distances and proportions on a map.
Another application of similarity is in architecture and design. Architects often use similar triangles to determine the proportions and dimensions of buildings. By maintaining the ratios between different parts of a structure, architects can create visually appealing and harmonious designs.
Similarity is also essential in the field of medical imaging. When taking X-ray or MRI scans, doctors need to accurately measure the size and location of tumors or abnormalities. By using similar triangles, medical professionals can determine the dimensions of these structures without invasive procedures.
In conclusion, similarity is a powerful tool that has many practical applications in various fields. It allows us to accurately represent the real world, design visually pleasing structures, and make precise measurements. By understanding and applying the principles of similarity, we can gain valuable insights and solve complex problems in our everyday lives.