
In geometry, the volume of a solid is a measure of the amount of space it occupies. In this article, we will be focusing on the volume of prisms and cylinders, two common geometric solids.
A prism is a solid with two congruent polygonal bases and flat faces called lateral faces. The volume of a prism can be found by multiplying the area of the base (B) by the height (h). This can be represented by the formula V = Bh, where V is the volume of the prism.
A cylinder is a solid with two congruent circular bases and a curved surface. The volume of a cylinder can be found by multiplying the area of the base (B) by the height (h). This can be represented by the formula V = Bh, where V is the volume of the cylinder.
In this answer key, you will find the solutions to various problems involving the volume of prisms and cylinders. These solutions will help you understand the concepts and calculations involved in finding the volume of these geometric solids.
By practicing these problems and understanding the formulas, you will be able to confidently calculate the volume of prisms and cylinders in any given situation. Whether you are studying for a math test or simply want to expand your knowledge, this answer key will be a valuable resource for you.
Understanding the concept of volume
The concept of volume is an important aspect of geometry and is used to measure the amount of space occupied by a three-dimensional object, such as a prism or a cylinder. Volume is often expressed in cubic units and can be calculated using the appropriate formulas.
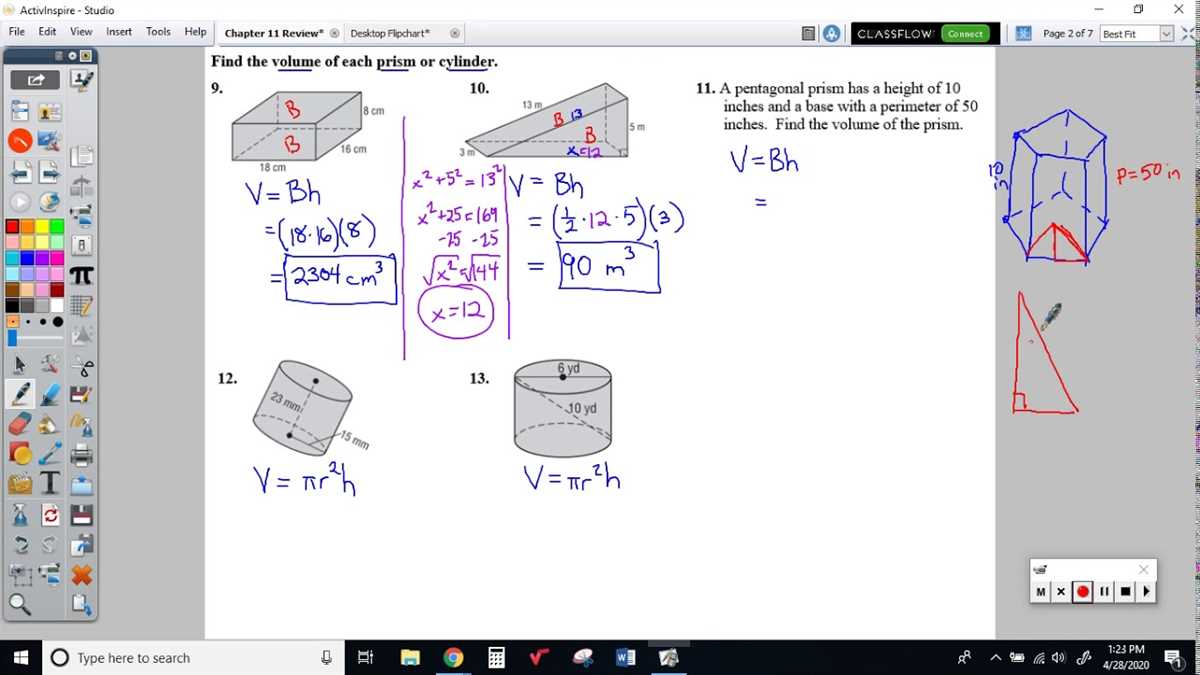
To find the volume of a prism, the formula V = Bh is used, where B represents the base area of the prism and h represents the height of the prism. This formula can be applied to various prisms, such as rectangular prisms, triangular prisms, or even irregular prisms. By calculating the area of the base and multiplying it by the height, the volume of the prism can be determined.
Similarly, the volume of a cylinder can be found using the formula V = πr^2h, where r represents the radius of the cylinder’s base and h represents the height of the cylinder. This formula applies to all cylinders, regardless of their shape. By calculating the area of the base (πr^2) and multiplying it by the height, the volume of the cylinder can be determined.
Understanding the concept of volume is crucial in many real-life applications, such as determining the amount of liquid a container can hold or calculating the volume of materials needed for construction projects. By mastering the formulas and concepts related to volume, individuals can accurately measure and calculate the space occupied by three-dimensional objects, contributing to various fields such as architecture, engineering, and manufacturing.
Calculating the volume of prisms

The volume of a prism is a measure of the space occupied by the prism. It is calculated by multiplying the base area of the prism by its height. The base can be any polygon, such as a triangle, rectangle, or pentagon, and the height is the perpendicular distance between the bases.
To calculate the volume of a prism, you need to know the dimensions of its base and its height. For example, if the base of a rectangular prism has a length of 5 units and a width of 3 units, and the height is 7 units, the volume can be calculated using the formula:
Volume = base area * height
In this case, the base area would be 5 units * 3 units = 15 square units, and the volume would be 15 square units * 7 units = 105 cubic units.
You can also calculate the volume of other types of prisms, such as triangular or hexagonal prisms, using similar formulas. The key is to find the base area and multiply it by the height.
It is important to note that the units for volume are always cubed, such as cubic units or cubic centimeters, because volume is a measure of three-dimensional space.
Applying the formula to real-life examples

The formula for finding the volume of prisms and cylinders can be applied to various real-life situations, helping us calculate the amount of space inside different objects. Let’s explore a few examples and see how the formula can be used.
Example 1: Fish Tank
Imagine you have a rectangular fish tank that measures 20 inches in length, 12 inches in width, and 10 inches in height. To find the volume of the fish tank, we can use the formula V = lwh, where V represents the volume, l is the length, w is the width, and h is the height. Plugging in the given values, we get V = 20 * 12 * 10 = 2400 cubic inches. Therefore, the fish tank can hold 2400 cubic inches of water.
Example 2: Can of Soup
Consider a cylindrical can of soup with a radius of 3 inches and a height of 5 inches. To calculate the volume of the can, we can use the formula V = πr^2h, where V is the volume, π is a constant (approximately equal to 3.14), r is the radius, and h is the height. Applying the formula, we get V = 3.14 * 3^2 * 5 = 141.3 cubic inches. Therefore, the can of soup can hold approximately 141.3 cubic inches of soup.
In conclusion, the formula for finding the volume of prisms and cylinders can be used in many real-life scenarios. Whether it’s determining the capacity of a fish tank or calculating the amount of soup in a can, the formula provides a practical way to measure volume.
Finding the volume of cylinders
A cylinder is a three-dimensional geometric shape that consists of two parallel circular bases connected by a curved surface. The volume of a cylinder is the amount of space it occupies. To find the volume of a cylinder, you need to know the radius of its base and its height.
The formula for finding the volume of a cylinder is V = πr^2h, where V represents the volume, π is a mathematical constant that approximately equals 3.14, r is the radius of the cylinder’s base, and h is the height of the cylinder.
To calculate the volume of a cylinder, follow these steps:
- Identify the radius of the cylinder’s base and the height of the cylinder.
- Square the radius value.
- Multiply the squared radius by the height of the cylinder.
- Multiply the result by the value of π (approximately 3.14).
- The final value obtained is the volume of the cylinder.
For example, let’s consider a cylinder with a radius of 3 units and a height of 5 units:
- The radius is 3 units and the height is 5 units.
- Squaring the radius gives us 9.
- Multiplying 9 by the height of 5 gives us 45.
- Multiplying 45 by the value of π (approximately 3.14) gives us a final volume of approximately 141.3 cubic units.
Therefore, the volume of the given cylinder is approximately 141.3 cubic units.
Understanding how to calculate the volume of cylinders is important in various real-life applications, such as engineering, architecture, and manufacturing, where determining the amount of space occupied by cylindrical objects is necessary for design and construction purposes.
Solving Practice Problems
Now that we have learned about finding the volume of prisms and cylinders, let’s put our knowledge into practice by solving some problems. Below are a few practice problems along with their solutions:
Practice Problem 1:
Find the volume of a rectangular prism with length 5 cm, width 3 cm, and height 10 cm.
Solution:
- Remember that the formula to find the volume of a rectangular prism is V = lwh.
- Plug the given values into the formula:
- l = 5 cm
- w = 3 cm
- h = 10 cm
- Calculate the volume:
- V = 5 cm * 3 cm * 10 cm
- V = 150 cm³
- Therefore, the volume of the rectangular prism is 150 cm³.
Practice Problem 2:
Find the volume of a cylinder with radius 4 cm and height 6 cm.
Solution:
- Remember that the formula to find the volume of a cylinder is V = πr²h.
- Plug the given values into the formula:
- r = 4 cm
- h = 6 cm
- Calculate the volume:
- V = π * (4 cm)² * 6 cm
- V ≈ 301.59 cm³ (rounded to two decimal places)
- Therefore, the volume of the cylinder is approximately 301.59 cm³.
By practicing these problems, you can strengthen your understanding of finding the volume of prisms and cylinders. Remember to apply the appropriate formulas and units of measurement to solve each problem accurately.
Q&A:
How can I improve my problem-solving skills?
There are several ways to improve problem-solving skills. First, start by practicing regularly by solving various types of problems. This can be done through exercises, puzzles, or even participating in problem-solving competitions. Additionally, it’s important to analyze and learn from your mistakes and understand the strategies used to solve different types of problems. Finally, seek out resources such as books, online courses, or workshops that focus on problem-solving techniques.
What are some effective problem-solving strategies?
There are several effective problem-solving strategies that can be used depending on the situation. Some common strategies include breaking down the problem into smaller parts, brainstorming possible solutions, and using logical reasoning to eliminate options. Additionally, collaborating with others and seeking different perspectives can often lead to innovative solutions. It’s also important to stay organized, stay focused, and be open to learning from failures.
How can I overcome the fear of difficult practice problems?
Overcoming the fear of difficult practice problems takes time and practice. One strategy is to break down the problem into smaller, more manageable parts. By focusing on solving one part at a time, the problem becomes less daunting. Additionally, it’s important to take a positive mindset and view difficult problems as opportunities for growth and learning. Seeking guidance from teachers, mentors, or classmates can also help in understanding and solving difficult problems.
What should I do if I get stuck on a practice problem?
If you get stuck on a practice problem, it’s important to first take a step back and assess your approach. Double-check if you have understood the problem correctly and review any relevant concepts. If you still can’t make progress, it can be helpful to take a break and come back to the problem later with a fresh perspective. You can also try discussing the problem with a peer, teacher, or an online community for additional insights and guidance.