Special right triangles pose an interesting challenge in the realm of mathematics. These triangles, which have specific angle measures and side lengths, hold secrets waiting to be unlocked by those with the knowledge and skill to decipher their mysteries. In this article, we will delve into the world of puzzle math and explore the answer key to unravel the enigma of special right triangles.
Special right triangles are a unique subset of triangles that have angles measuring exactly 30, 45, or 60 degrees. These triangles also have side lengths that follow a specific pattern. One common type of special right triangle is the 45-45-90 triangle, where the two acute angles are both 45 degrees, and the sides follow a ratio of 1:1:√2. Another well-known special right triangle is the 30-60-90 triangle, where the angles measure 30, 60, and 90 degrees, and the sides follow a ratio of 1:√3:2.
The answer key to puzzle math special right triangles lies in understanding the relationships between the angles and side lengths. By recalling basic trigonometric functions such as sine, cosine, and tangent, one can deduce missing side lengths or angle measures. Additionally, recognizing the patterns and ratios within special right triangles can provide shortcuts to solve complex problems.
Mastering the puzzle math of special right triangles opens up a world of possibility in various fields of study. Architects can utilize these triangles to ensure structural stability and create aesthetically pleasing designs. Engineers can employ them in mechanical and electrical systems to optimize efficiency. Geometry enthusiasts can explore the elegance and beauty of these unique triangles, marveling at the symmetrical and harmonious nature of their proportions.
Puzzle Math Special Right Triangles Answer Key
In the study of geometry, special right triangles play an important role in solving various problems. These triangles have angles of 45-45-90 degrees and 30-60-90 degrees, which make them unique and easy to work with. The puzzle math special right triangles answer key provides the solutions to a range of problems involving these special triangles.
The answer key includes step-by-step explanations for finding the missing side lengths and angles in special right triangles. It helps students understand the relationships between the different sides and angles of these triangles, and how to use trigonometric ratios to solve problems. The answer key also includes examples of real-world applications of special right triangles, such as finding the height of a tree or the length of a ladder against a wall.
The puzzle math special right triangles answer key can be used by teachers as a resource for lesson planning and instruction. It provides a comprehensive guide to teaching and learning about special right triangles, making it easier for educators to explain the concepts and engage students in problem-solving activities. The answer key can also be used by students as a study aid or reference tool when reviewing for exams or completing homework assignments.
In conclusion, the puzzle math special right triangles answer key is a valuable tool for understanding and solving problems involving special right triangles. It provides a clear and structured approach to working with these triangles, and helps students develop their mathematical reasoning and problem-solving skills. Whether you are a teacher or a student, the answer key can be a useful resource in mastering the concepts of special right triangles and applying them to real-world situations.
What are special right triangles?
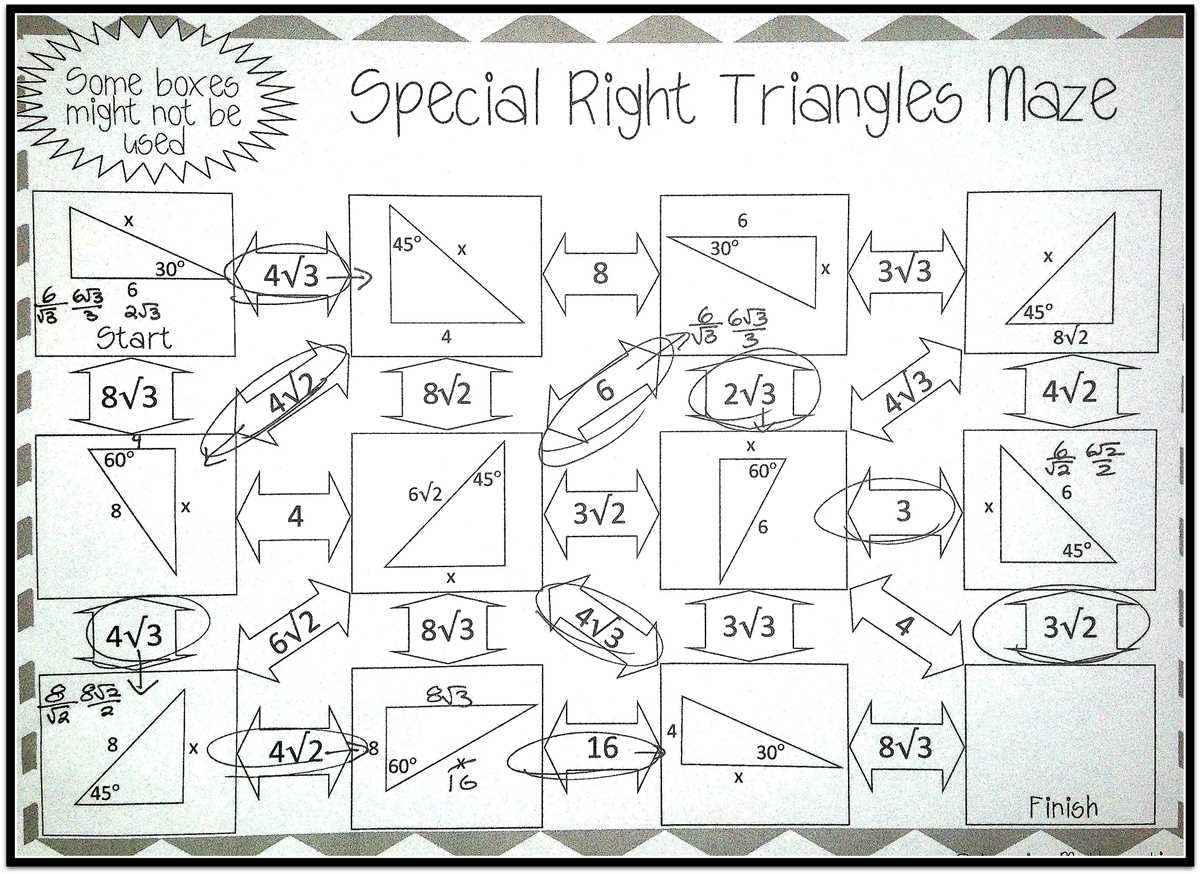
Special right triangles are a type of triangle that have certain properties which make them unique and useful in mathematical calculations. These triangles have angles that follow specific ratios, making their side lengths predictable and easy to calculate.
There are two types of special right triangles: the 45-45-90 triangle and the 30-60-90 triangle. The 45-45-90 triangle, also known as the isosceles right triangle, has two equal angles of 45 degrees and one right angle of 90 degrees. The side lengths of this triangle are in a ratio of 1:1:√2, where the length of the hypotenuse is equal to the length of either of the other two sides multiplied by the square root of 2.
The 30-60-90 triangle, also known as the right triangle, has angles measuring 30, 60, and 90 degrees. The side lengths of this triangle are in a ratio of 1:√3:2, where the length of the hypotenuse is equal to twice the length of the shorter side, and the length of the longer side is equal to the shorter side multiplied by the square root of 3.
These special right triangles are often used in trigonometry and geometry to solve complex problems involving angles and side lengths. By knowing the ratios of the side lengths in these triangles, mathematicians are able to quickly and accurately calculate unknown values, such as the lengths of sides and the measures of angles.
How to identify special right triangles?

Special right triangles are a type of triangle that have specific properties and ratios that can make them easier to solve. There are two types of special right triangles: the 45-45-90 triangle and the 30-60-90 triangle.
The 45-45-90 triangle is a right triangle with two equal angles of 45 degrees each. The sides of this triangle have a specific length ratio: the length of the hypotenuse is equal to the length of the legs multiplied by the square root of 2. The legs of this triangle are also equal in length.
The 30-60-90 triangle is a right triangle with angles of 30 degrees, 60 degrees, and 90 degrees. The sides of this triangle also have a specific length ratio: the length of the hypotenuse is equal to twice the length of the shorter leg, and the length of the longer leg is equal to the shorter leg multiplied by the square root of 3.
To identify if a triangle is a special right triangle, you can look for clues in the angle measures or ratio of side lengths. If the triangle has angles of 45 degrees and 45 degrees, it is a 45-45-90 triangle. If the triangle has angles of 30 degrees, 60 degrees, and 90 degrees, it is a 30-60-90 triangle. You can also calculate the ratio of side lengths to see if it matches the properties of a special right triangle.
Identifying special right triangles can be useful in solving math problems and finding missing side lengths or angles. Once you recognize a triangle as a special right triangle, you can use the specific ratios and properties to simplify calculations and find solutions more efficiently.
Properties of special right triangles
Special right triangles are a category of right triangles that have specific properties and relationships among their sides and angles. These triangles include the 45-45-90 triangle and the 30-60-90 triangle. Understanding the properties of these triangles can be useful in solving problems involving angles, side lengths, and areas.
The 45-45-90 triangle, also known as the isosceles right triangle, has two equal angles of 45 degrees and one right angle of 90 degrees. The sides of this triangle follow a specific ratio: the length of the hypotenuse is equal to the length of either leg times the square root of 2. This can be written as: c = a√2, where c is the length of the hypotenuse and a is the length of each leg.
The 30-60-90 triangle, also known as the right triangle of half an equilateral triangle, has angles measuring 30, 60, and 90 degrees. The side lengths of this triangle also follow a specific ratio: the length of the hypotenuse is equal to twice the length of the shorter leg, and the length of the longer leg is equal to the length of the shorter leg times the square root of 3. This can be written as: c = 2a and b = a√3, where c is the length of the hypotenuse, a is the length of the shorter leg, and b is the length of the longer leg.
These properties can be used to solve various mathematical problems involving special right triangles. By knowing the ratios of the side lengths, it becomes easier to calculate missing lengths or angles in a triangle. Additionally, the relationship between the angles can help in determining the type of special right triangle and its corresponding properties.
Overall, understanding the properties of special right triangles can be a valuable tool in solving geometry problems and furthering one’s understanding of right triangle relationships and trigonometry.
Applying special right triangles in problem solving
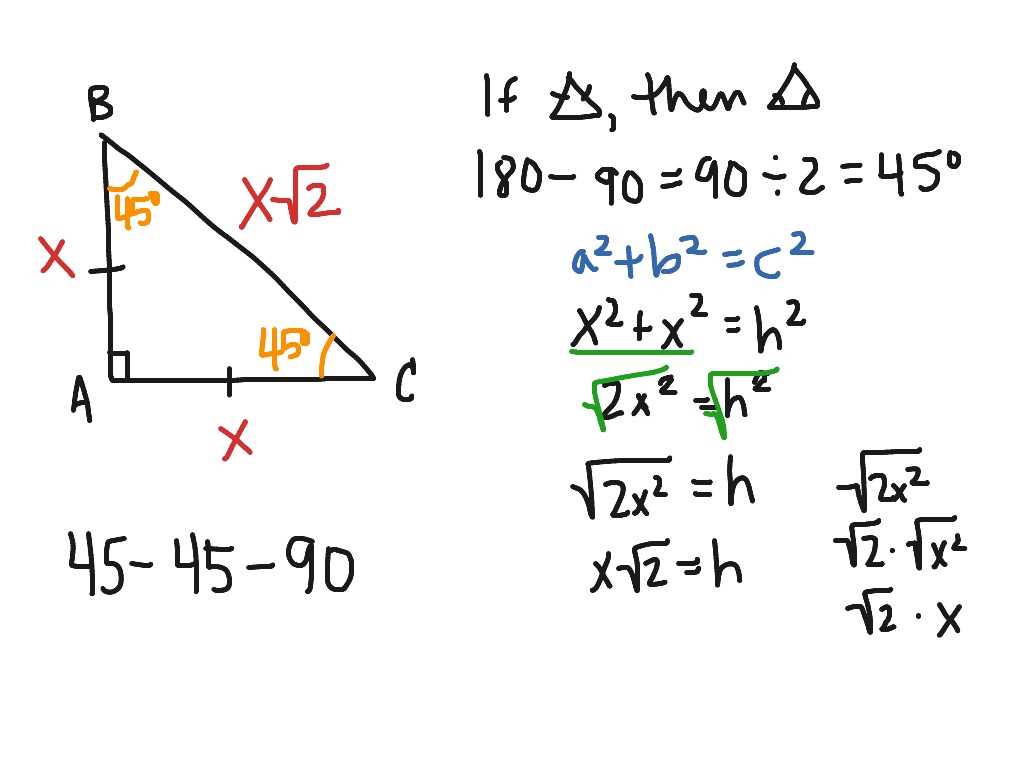
Special right triangles, namely the 45-45-90 triangle and the 30-60-90 triangle, are fundamental tools in problem solving involving geometry and trigonometry. These triangles offer unique relationships between their side lengths and angles, making them valuable in various applications.
In problem solving, special right triangles can be used to find missing side lengths or angles, calculate areas, and solve trigonometric equations. Their properties allow for simplification of complex calculations and provide a systematic approach to solving problems.
For example, when dealing with a 45-45-90 triangle, it is helpful to know that the two legs are congruent and the hypotenuse is √2 times the length of the legs. This information can be used to find the length of a missing side or calculate the area of the triangle.
Similarly, in a 30-60-90 triangle, the ratio of the side lengths is 1 : √3 : 2. This ratio can be used to find missing side lengths or angles, as well as calculate the area of the triangle.
By recognizing and applying the properties of special right triangles, problem solvers can simplify complex scenarios and find efficient solutions. These triangles serve as powerful tools in various mathematical disciplines, including algebra, geometry, and trigonometry, and their applications extend beyond the classroom into fields such as engineering and architecture.
Using the Puzzle Math Approach to Solve Special Right Triangles
The puzzle math approach is a useful method for solving special right triangles, which are triangles that contain angles of 30, 45, and 60 degrees. These triangles have specific ratios between their sides, making them easier to work with compared to general triangles.
To solve these types of triangles using the puzzle math approach, it is important to understand the relationships between the angles and sides. For example, in a 30-60-90 triangle, the side opposite the 30-degree angle is half the length of the hypotenuse, and the side opposite the 60-degree angle is the length of the hypotenuse multiplied by the square root of 3.
The puzzle math approach involves breaking down the triangle into smaller, more manageable parts. By visually splitting the triangle into smaller triangles or rectangles and using the known ratios and side lengths, you can determine the values of the missing sides. This method is particularly useful when dealing with complex cases or when working with non-standard right triangles.
By applying the puzzle math approach to special right triangles, you can quickly and accurately solve for unknown side lengths and angles. This method is an effective way to approach geometry problems and can help improve problem-solving skills in mathematics. Understanding the key ratios and relationships in special right triangles is essential for successfully using the puzzle math approach.
Answer key to Puzzle Math Special Right Triangles
Thank you for participating in the Puzzle Math Special Right Triangles! Below is the answer key to the puzzle:
- Question 1: Right triangle ABC, with a right angle at C, has sides AC = 8 units and BC = 6 units. Find the length of the hypotenuse, AB.
- Answer 1: The length of the hypotenuse AB is 10 units.
- Question 2: Right triangle XYZ, with a right angle at Z, has sides XZ = 15 units and YZ = 9 units. Find the length of the hypotenuse, XY.
- Answer 2: The length of the hypotenuse XY is 18 units.
- Question 3: Right triangle PQR, with a right angle at Q, has sides PQ = 5 units and QR = 12 units. Find the length of the hypotenuse, PR.
- Answer 3: The length of the hypotenuse PR is 13 units.
By solving these special right triangle problems, you have practiced applying the Pythagorean theorem and identifying the relationships between the sides of right triangles. Keep up the good work!