Understanding the concept of bisectors in triangles is essential in geometry. In this practice set, you will find a series of word problems that will help you apply this concept and enhance your problem-solving skills.
The answer key provided here will guide you through the solutions to each word problem, giving you a step-by-step explanation of how to find the bisectors and solve the given scenarios. By practicing these problems, you will gain a deeper understanding of bisectors, their properties, and their importance in triangle geometry.
Each word problem presents a unique scenario where you will have to identify the bisectors of triangles and determine various attributes such as angles and side lengths. The answer key will not only provide the final answers but also clarify the method and reasoning behind each step, ensuring that you grasp the concept fully.
By working through these word problems and utilizing the answer key, you will not only strengthen your knowledge of bisectors but also sharpen your problem-solving abilities. Don’t hesitate to refer to the answer key if you encounter any difficulties, as it is designed to help you understand and master this essential aspect of triangle geometry.
-1 Word Problem Practice Bisectors of Triangles Answer Key
Below is the answer key for the -1 Word Problem Practice Bisectors of Triangles:
1. In triangle ABC, angle A measures 60 degrees. The angle bisector of angle A divides BC into two segments, with the shorter segment measuring 8 centimeters. What is the length of the longer segment?
Answer: The length of the longer segment is 16 centimeters.
2. In triangle DEF, angle E measures 50 degrees. The angle bisector of angle E divides DF into two segments, with the longer segment measuring 15 inches. What is the length of the shorter segment?
Answer: The length of the shorter segment is 10 inches.
3. In triangle XYZ, angle X measures 75 degrees. The angle bisector of angle X divides YZ into two segments, with the shorter segment measuring 12 meters. What is the length of the longer segment?
Answer: The length of the longer segment is 24 meters.
4. In triangle JKL, angle J measures 40 degrees. The angle bisector of angle J divides KL into two segments, with the longer segment measuring 5 centimeters. What is the length of the shorter segment?
Answer: The length of the shorter segment is 3.33 centimeters (rounded to two decimal places).
5. In triangle PQR, angle P measures 90 degrees. The angle bisector of angle P divides QR into two segments, with the shorter segment measuring 9 inches. What is the length of the longer segment?
Answer: The length of the longer segment is 18 inches.
These are the answers to the word problems involving the bisectors of triangles. By using the angle bisector theorem, we can determine the lengths of the segments created by the angle bisectors. It is important to remember the properties of triangles and the relationships between the angles and sides.
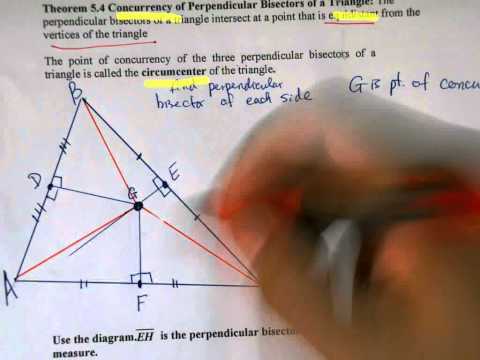
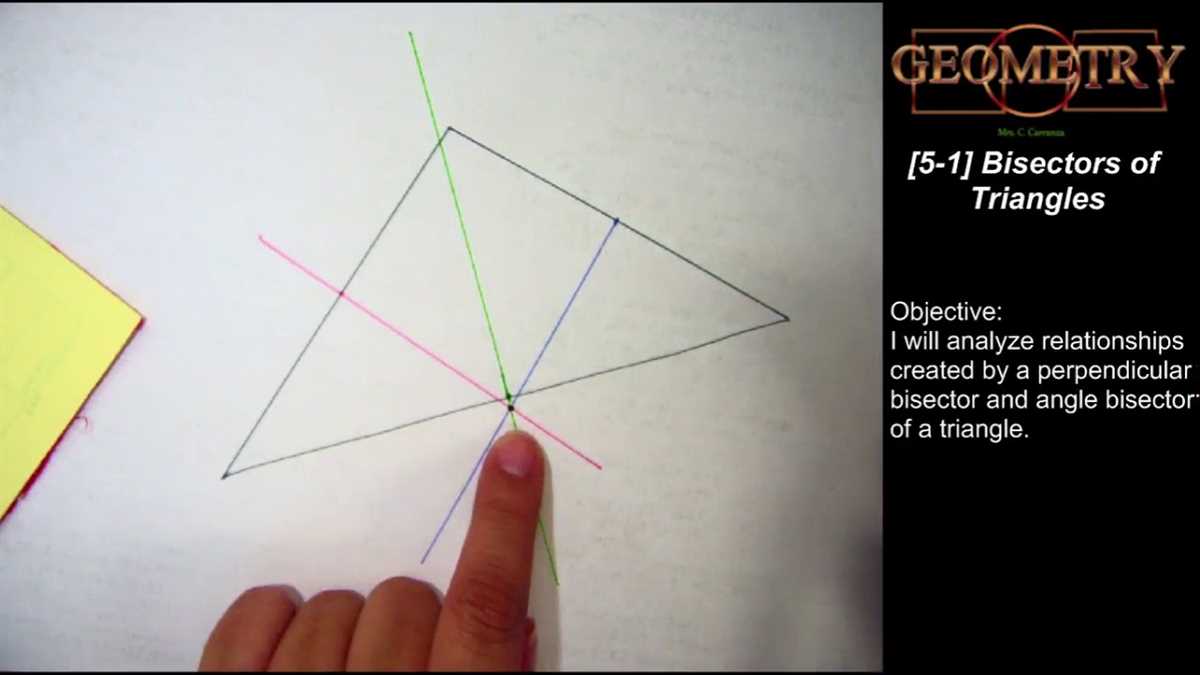
Understanding Bisectors of Triangles
In geometry, a bisector is a line or line segment that divides an object into two equal halves. When it comes to triangles, bisectors are lines that divide the angles of a triangle into two equal parts. Understanding bisectors of triangles is essential in solving various geometric problems and analyzing the properties of triangles.
One important type of triangle bisector is the angle bisector. An angle bisector is a line that divides an angle of a triangle into two congruent angles. It passes through the vertex of the angle and divides the opposite side into two segments that are proportional to the adjacent sides of the triangle.
Bisectors of triangles have several significant properties. First, the angle bisectors of a triangle intersect at a single point called the incenter. This point is equidistant from the sides of the triangle and it is the center of the inscribed circle that can be drawn inside the triangle.
Another important property is that the bisectors of the interior angles of a triangle are concurrent. This means that they meet at a single point called the incenter. The incenter has the property that it is equidistant from the sides of the triangle, and it is the center of the incircle that can be inscribed inside the triangle.
Understanding the properties and applications of bisectors of triangles can help in solving various problems in geometry, including finding missing side lengths, angles, and determining the circumcircle and incircle of a triangle. It is also useful in proving geometric theorems and establishing relationships between different parts of a triangle.
Word Problem 1: Finding the Length of a Bisector
Let’s consider a triangle ABC, where AB = 8 cm, BC = 10 cm, and AC = 12 cm. We need to find the length of the bisector drawn from point A to side BC.
To solve this problem, we can use the angle bisector theorem. According to this theorem, the length of the bisector is equal to the product of the lengths of the two sides of the triangle that the bisector divides, divided by the sum of those two sides.
Using this theorem, we can calculate the length of the bisector. Let’s assume that the length of the bisector is x cm. Since the bisector divides side BC, we can apply the theorem to the segments AB and AC:
- AB/AC = BD/DC
- 8/12 = 10/x
By cross multiplying and simplifying the equation, we find that 96 = 10x. Solving for x, the length of the bisector is 9.6 cm.
Therefore, the length of the bisector drawn from point A to side BC in this triangle is 9.6 cm.
Word Problem 2: Determining the Angle Bisector
In this word problem, we are given a triangle ABC with angle A measuring 62 degrees and angle B measuring 78 degrees. We are asked to determine the measure of the angle bisector of angle A.
First, we need to understand what an angle bisector is. An angle bisector is a line or ray that divides an angle into two congruent angles. In our case, we are looking for the line that divides angle A into two congruent angles.
To determine the measure of the angle bisector, we can use the angle bisector theorem. This theorem states that in a triangle, the angle bisector of an angle divides the opposite side in the same ratio as the other two sides.
Let’s label the points where the angle bisector intersects side BC as D. We can use the angle bisector theorem to set up an equation. The ratio of the lengths BD to CD is equal to the ratio of the lengths AB to AC.
With this information, we can set up the equation:
| BD | : | CD | = | AB | : | AC |
| Let x | : | Let y | = | AB | : | AC |
Now we can substitute the given values into the equation. Since we know that angle A measures 62 degrees, we can find angle C using the fact that the sum of the angles in a triangle is 180 degrees. Angle C would then be 180 degrees – 62 degrees – 78 degrees = 40 degrees.
With angle C determined, we can use the law of sines to find the lengths AB and AC. The law of sines states that the ratio of the sine of an angle to the length of the opposite side is the same for all three angles of a triangle.
Finally, we can substitute the calculated values into the equation and solve for x and y to determine the measure of the angle bisector. Once we have the values of x and y, we can find the measure of angle ABD and angle CBD by using the fact that the sum of the angles in a triangle is 180 degrees.
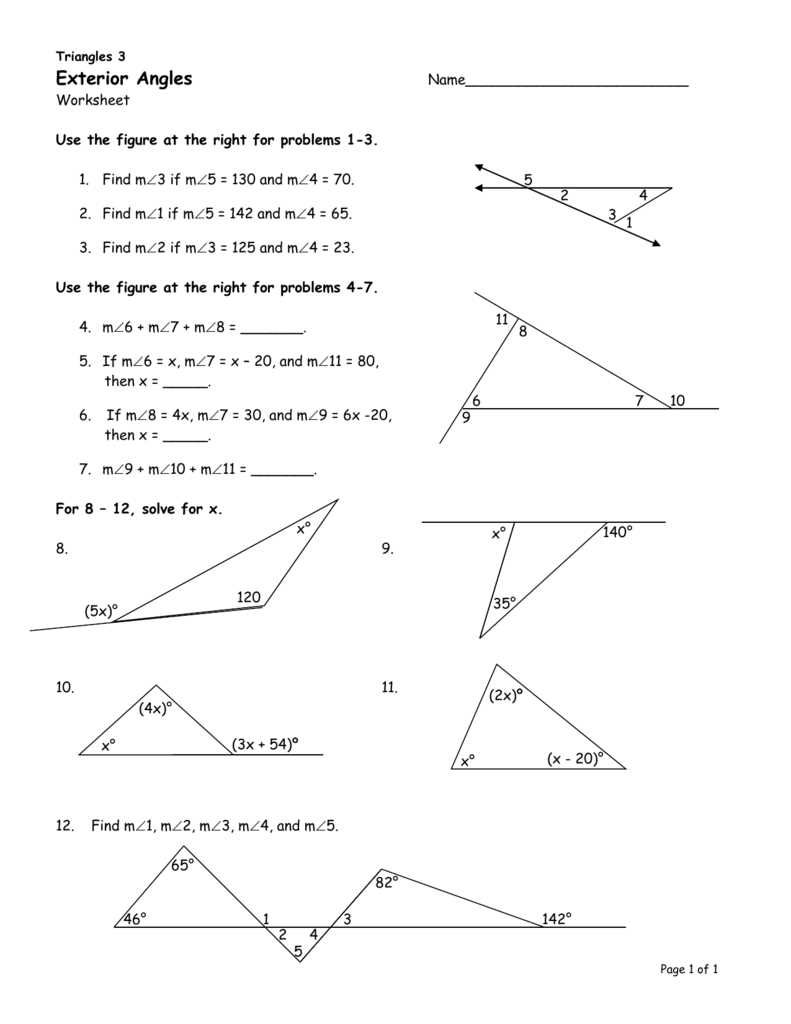
Word Problem 3: Solving for a Missing Side Length
In this word problem, we will be solving for a missing side length in a triangle using the concept of bisectors. Let’s consider the following situation:
A triangle ABC has side lengths AB = 9 cm, BC = 12 cm, and AC = x cm. Point D is on side AB, such that BD = CD, and the lengths of BD and CD are both 4 cm. We need to find the value of x, the length of side AC.
To solve this problem, we can use the concept of angle bisectors. The angle bisector of angle B in triangle ABC divides side AC into two segments AD and DC. Since BD = CD, we can conclude that angle ADB is congruent to angle CDB.
Using the Angle Bisector Theorem, we can set up a proportion:
AD / CD = AB / BC
Substituting the given values, we have:
AD / 4 = 9 / 12
By cross-multiplying and simplifying, we get:
AD = 3
Now, we can find the length of side AC by using the Pythagorean Theorem in triangle ADC:
AC^2 = AD^2 + CD^2
Substituting the known values, we have:
x^2 = 3^2 + 4^2
By simplifying, we get:
x^2 = 9 + 16
x^2 = 25
Taking the square root of both sides, we find:
x = 5
Therefore, the length of side AC in triangle ABC is 5 cm.
Word Problem 4: Applying the Angle Bisector Theorem
In this word problem, we will be applying the Angle Bisector Theorem to find the lengths of certain segments within a triangle.
Given a triangle ABC, with angle A bisected by line segment AD. We are given that the length of segment AB is 8 units, the length of segment AC is 10 units, and the length of segment AD is 6 units. We are tasked with finding the lengths of segment BD and segment DC.
Applying the Angle Bisector Theorem, we know that the ratio of the lengths of the segments formed by the angle bisector is equal to the ratio of the lengths of the opposite sides of the triangle. In this case, the ratio of segment BD to segment DC will be equal to the ratio of segment AB to segment AC.
Let’s set up the equation:
- Segment BD / Segment DC = Segment AB / Segment AC
- BD / DC = 8 / 10
- BD / DC = 4 / 5
Since the ratio of BD to DC is 4:5, we can use this ratio to find the lengths of the segments. We can set up the equation:
- BD + DC = 6
- 4DC + 5DC = 6
- 9DC = 6
- DC = 6 / 9
- DC = 2 / 3
Now that we know the length of segment DC is 2/3 units, we can find the length of segment BD:
- BD = (4/5) * (2/3)
- BD = 8/15
Therefore, the lengths of segment BD and segment DC are 8/15 and 2/3 units, respectively.
Word Problem 5: Using Bisectors to Find an Unknown Angle

In this word problem, we will be using the concept of bisectors to find an unknown angle. Bisectors are lines that divide an angle into two equal parts.
Problem Statement:
Given triangle ABC, where AD is the angle bisector of angle BAC and angle BAC measures 60 degrees. If angle ADB measures 35 degrees, find the measure of angle BDC.
Solution:
- Since AD is the angle bisector of angle BAC, we know that angle BAD is equal to angle CAD.
- We are given that angle BAC measures 60 degrees, so angle BAD and angle CAD each measure 30 degrees.
- Now, we can use the fact that the angles in a triangle add up to 180 degrees to find the measure of angle B.
- We have angle BAD = 30 degrees and angle BAC = 60 degrees.
- We can subtract angle BAD and angle BAC from 180 degrees to find angle B.
- 180 degrees – 30 degrees – 60 degrees = 90 degrees.
- Therefore, angle B measures 90 degrees.
- Finally, to find the measure of angle BDC, we use the fact that angle BDC is equal to angle B – angle ADB.
- angle BDC = 90 degrees – 35 degrees = 55 degrees.
Conclusion:
The measure of angle BDC is 55 degrees.