
Trigonometry is a branch of mathematics that deals with the relationships between the angles and sides of triangles. It has various applications in fields such as engineering, physics, and navigation. One of the important concepts in trigonometry is the trigonometric ratios, which help in solving problems related to angles and sides of a triangle.
The trigonometric ratios include sine, cosine, tangent, cosecant, secant, and cotangent. These ratios help in determining the relationship between the lengths of the sides and the measure of the angles in a right triangle. The value of each trigonometric ratio can be found by using a calculator or by referring to a trigonometric table. However, it is important to understand how these ratios are derived and how to find their values manually.
This article provides the answer key for finding the value of each trigonometric ratio. It includes step-by-step explanations and examples to help you understand the process. By mastering these ratios, you will be able to solve various trigonometry problems and apply them to real-life situations. So, let’s dive in and explore the world of trigonometric ratios!
Find the Value of Each Trigonometric Ratio Answer Key

Trigonometric ratios are mathematical functions that relate the angles of a triangle to the ratio of the lengths of its sides. These ratios are widely used in various fields such as physics, engineering, and navigation. To find the value of each trigonometric ratio, one must have knowledge of the angle and the lengths of the sides of the triangle.
The answer key to finding the value of each trigonometric ratio provides a guide to solving the problems and finding the correct answers. It includes steps and explanations for each calculation, ensuring that students understand the process and reach the correct solution.
Here is an example of a trigonometric ratio problem and its corresponding answer key:
-
Problem: Find the sine, cosine, and tangent of angle A in a right triangle with side lengths of 3, 4, and 5.
Angle A: ? Side lengths: a = 3, b = 4, c = 5 Answer Key:
- Sine: sin(A) = opposite/hypotenuse = 3/5
- Cosine: cos(A) = adjacent/hypotenuse = 4/5
- Tangent: tan(A) = opposite/adjacent = 3/4
By using the answer key, students can check their work and ensure that they have correctly calculated the trigonometric ratios. It also serves as a valuable learning tool, as students can review the steps and explanations to understand the concepts better.
Overall, the answer key for finding the value of each trigonometric ratio is a useful resource for students studying trigonometry. It provides guidance, explanations, and a step-by-step approach to solving trigonometric ratio problems, helping students develop a deeper understanding of the topic.
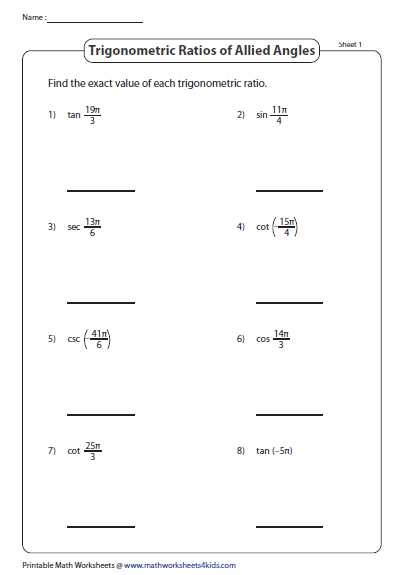
Trigonometric Ratios for Common Angles

Trigonometric ratios are an essential part of trigonometry and are used to relate the angles of a right triangle to the lengths of its sides. These ratios can be calculated for any angle, but there are certain angles for which the ratios have commonly known values. These angles are often referred to as “common angles” and include 0°, 30°, 45°, 60°, and 90°.
Sine, cosine, and tangent are three fundamental trigonometric ratios that relate the angles of a right triangle to the ratio of the lengths of its sides. For the common angles mentioned above, these ratios can be easily determined:
- For 0°, the sine is 0, the cosine is 1, and the tangent is 0.
- For 30°, the sine is 0.5, the cosine is √3/2, and the tangent is √3/3.
- For 45°, the sine is √2/2, the cosine is √2/2, and the tangent is 1.
- For 60°, the sine is √3/2, the cosine is 0.5, and the tangent is √3.
- For 90°, the sine is 1, the cosine is 0, and the tangent is undefined.
These values are widely used in trigonometry and can be used to solve problems involving angles and sides of right triangles. By knowing these common trigonometric ratios, students can quickly find the values of sine, cosine, and tangent for these specific angles.
Finding Trigonometric Ratios using Special Right Triangles
Trigonometric ratios, such as sine, cosine, and tangent, are used to relate the angles of a right triangle to the lengths of its sides. These ratios are often used in geometry and physics to solve problems involving right triangles. One way to find the values of these ratios is by using special right triangles.
Special right triangles are triangles with angles that have specific values, making their lengths ratios of each other. Two special right triangles that are commonly used are the 45-45-90 triangle and the 30-60-90 triangle.
45-45-90 Triangle:
In a 45-45-90 triangle, both the acute angles are 45 degrees. This means that the sides opposite these angles are equal in length. The longest side, called the hypotenuse, is always sqrt(2) times the length of either of the other two sides. Using these ratios, we can find the values of sine, cosine, and tangent of 45 degrees.
- Sine of 45 degrees: sin(45) = 1/sqrt(2) = sqrt(2)/2
- Cosine of 45 degrees: cos(45) = 1/sqrt(2) = sqrt(2)/2
- Tangent of 45 degrees: tan(45) = 1
30-60-90 Triangle:
In a 30-60-90 triangle, the angles are 30 degrees, 60 degrees, and 90 degrees. The side opposite the 30-degree angle is half the length of the hypotenuse, and the side opposite the 60-degree angle is sqrt(3) times the length of the side opposite the 30-degree angle. Using these ratios, we can find the values of sine, cosine, and tangent of 30 and 60 degrees.
- Sine of 30 degrees: sin(30) = 1/2
- Cosine of 30 degrees: cos(30) = sqrt(3)/2
- Tangent of 30 degrees: tan(30) = 1/sqrt(3) = sqrt(3)/3
- Sine of 60 degrees: sin(60) = sqrt(3)/2
- Cosine of 60 degrees: cos(60) = 1/2
- Tangent of 60 degrees: tan(60) = sqrt(3)
Using the values of sine, cosine, and tangent obtained from special right triangles, we can easily find the values of these trigonometric ratios for any given angle within the range of 0 to 90 degrees.
Finding Trigonometric Ratios using the Unit Circle
Trigonometric ratios, such as sine, cosine, and tangent, are mathematical functions that relate the angles of a right triangle to the lengths of its sides. These ratios are widely used in various fields, including physics, engineering, and navigation. One way to find these ratios is by using the unit circle.
The unit circle is a circle with a radius of 1 unit. It is centered at the origin of a Cartesian coordinate system. By using the unit circle, we can relate the coordinates of points on the circle to the values of sinusoidal functions. The x-coordinate of a point on the unit circle represents the cosine of the corresponding angle, while the y-coordinate represents the sine of the angle.
In order to find the values of trigonometric ratios using the unit circle, we need to associate each angle with a point on the unit circle. Starting from the positive x-axis, we can move counterclockwise around the circle, measuring angles in radians or degrees. As we move around the circle, we can determine the values of sine, cosine, and tangent for each angle by looking at the coordinates of the corresponding points on the circle.
For example, at the angle of 30 degrees (or π/6 radians), the corresponding point on the unit circle has coordinates (cos(30°), sin(30°)). By evaluating these trigonometric functions, we can find the exact values of sine and cosine for this angle. Similarly, the tangent of an angle can be found by dividing the sine of the angle by the cosine of the angle.
The unit circle provides a visual representation of the trigonometric ratios and helps in understanding their values for various angles. By memorizing the key angles and their corresponding trigonometric ratios, we can quickly find the values of these ratios for any given angle.
Using Trigonometric Ratios to Solve Problems
Trigonometric ratios provide a powerful tool for solving a wide range of problems involving angles and relationships between sides of triangles. By understanding and utilizing these ratios, we can find missing lengths or angles, determine the height of objects, and solve various real-world problems.
One commonly used trigonometric ratio is the sine ratio, which is defined as the ratio of the length of the side opposite the angle to the length of the hypotenuse. This ratio can be used to find missing angles or side lengths in right triangles. For example, if we know the lengths of two sides in a right triangle, we can use the sine ratio to find the measure of an angle.
Another important ratio is the cosine ratio, which is defined as the ratio of the length of the adjacent side to the length of the hypotenuse. The cosine ratio can be used to find missing side lengths or angles in right triangles. For instance, if we know the length of the hypotenuse and one side, we can use the cosine ratio to find the length of the other side.
Additionally, the tangent ratio, which is defined as the ratio of the length of the side opposite the angle to the length of the side adjacent to the angle, is also widely used. This ratio can help us find angles or side lengths in right triangles. For example, if we know the lengths of the two sides, we can use the tangent ratio to find the measure of an angle.
By applying these trigonometric ratios and understanding their relationships, we can solve various problems related to triangles and angles. Whether it’s determining the height of a building, finding the distance between two points, or calculating the trajectory of a projectile, trigonometric ratios provide a valuable tool for solving complex problems in a precise and efficient manner.
Wrapping Up: Key Takeaways on Trigonometric Ratios
Trigonometric ratios are mathematical functions that relate the angles of a right triangle to the lengths of its sides. They are widely used in various fields, including geometry, physics, and engineering. Understanding and being able to calculate trigonometric ratios is essential for solving problems involving triangles and angles.
Here are some key takeaways on trigonometric ratios:
- Sine (sin): The sine of an angle is the ratio of the length of the side opposite the angle to the length of the hypotenuse.
- Cosine (cos): The cosine of an angle is the ratio of the length of the adjacent side to the length of the hypotenuse.
- Tangent (tan): The tangent of an angle is the ratio of the length of the opposite side to the length of the adjacent side.
- Cosecant (csc), Secant (sec), and Cotangent (cot): These are the reciprocal functions of sine, cosine, and tangent, respectively.
- Trigonometric identities: There are various identities and relationships involving trigonometric ratios, such as the Pythagorean identity (sin²θ + cos²θ = 1) and the sum and difference formulas.
- Unit circle: The unit circle is a circle with a radius of 1 centered at the origin of a coordinate plane. It is used to define the values of trigonometric ratios for any angle.
- Trigonometric tables and calculators: Trigonometric tables and electronic calculators can be used to find the values of trigonometric ratios for specific angles.
By understanding and applying these concepts, you will be able to confidently find the values of trigonometric ratios and use them to solve a variety of mathematical problems. Practice and familiarity with trigonometric ratios will help improve your problem-solving skills and enhance your understanding of geometry and trigonometry.