
The midpoint and distance formula are fundamental concepts in mathematics that are used to determine the position and separation between two points on a coordinate plane. These formulas enable us to calculate the midpoint between two points, as well as the distance between them, with ease and accuracy.
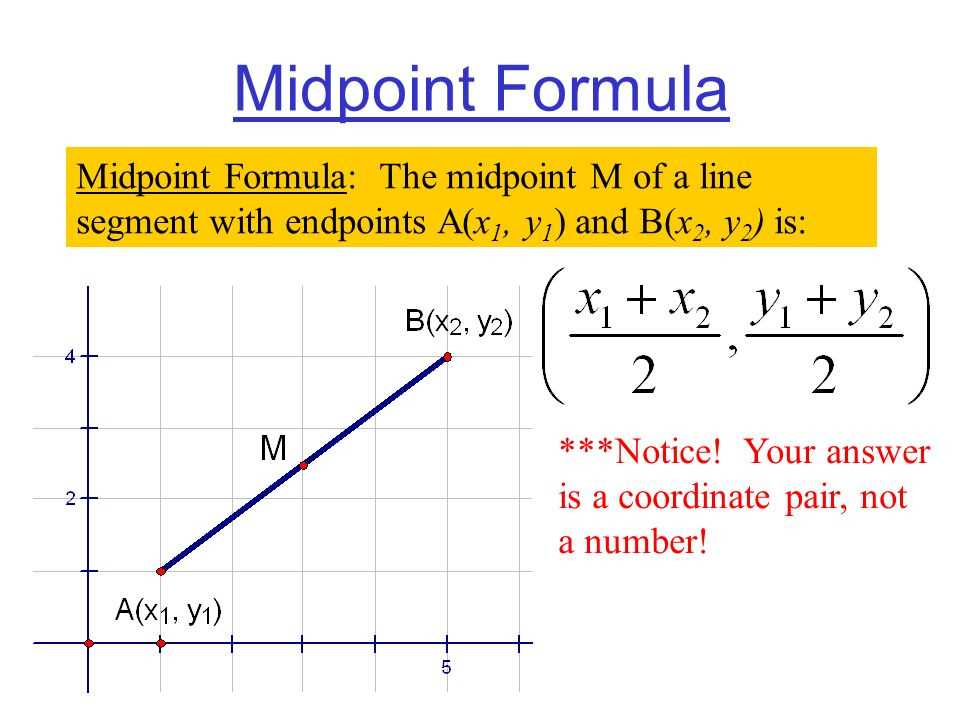
The midpoint formula states that the coordinates of the midpoint between two points (x1, y1) and (x2, y2) can be found by taking the average of their respective x-coordinates and y-coordinates. This can be expressed as:
Midpoint = [(x1 + x2)/2, (y1 + y2)/2]
On the other hand, the distance formula allows us to quantify the separation between two points. It is derived from the Pythagorean theorem and states that the distance between two points (x1, y1) and (x2, y2) is the square root of the sum of the squares of the differences between their respective x-coordinates and y-coordinates. Mathematically, the distance formula can be written as:
Distance = √[(x2 – x1)^2 + (y2 – y1)^2]
By mastering the midpoint and distance formula, one can solve various mathematical problems, such as finding the halfway point between two locations on a map or calculating the length of a line segment. These formulas are also essential in fields such as physics and engineering, where accurate spatial measurements are crucial.
Understanding the Midpoint and Distance Formula – Answer Key
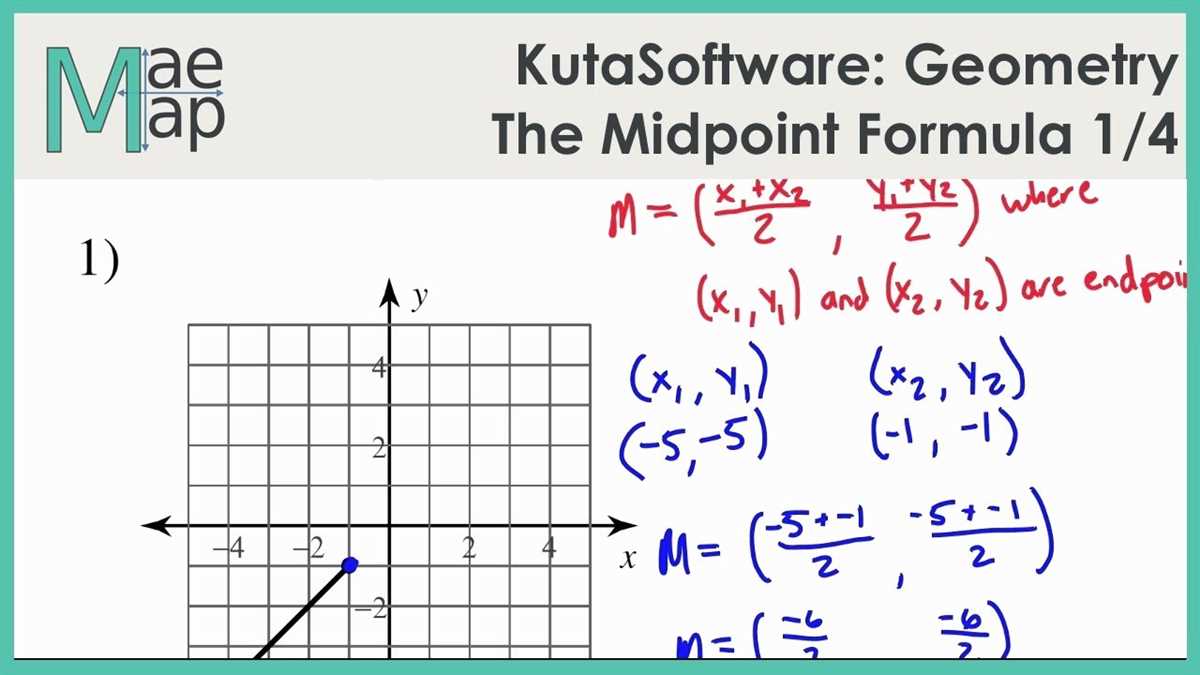
The midpoint and distance formulas are fundamental tools in geometry and algebra that help us calculate the coordinates of a point given its distance from other points or the midpoint between two points. This answer key provides a step-by-step solution for each problem in the exercise, allowing students to check their work and gain a deeper understanding of the concepts.
The midpoint formula allows us to find the coordinates of the midpoint of a line segment by taking the average of the x-coordinates and the y-coordinates of the endpoints. In the answer key, each step of the calculation is clearly shown, making it easier for students to follow along and replicate the process with other problems.
Example:

- Problem: Find the midpoint of the line segment with endpoints A(2, 4) and B(6, 8).
- Solution:
- Let’s label the x-coordinates of the endpoints as x1 and x2, and the y-coordinates as y1 and y2.
- Plug the values into the midpoint formula: x = (x1 + x2) / 2 and y = (y1 + y2) / 2.
- Calculate the midpoint coordinates: x = (2 + 6) / 2 = 4 and y = (4 + 8) / 2 = 6.
- Therefore, the midpoint of the line segment AB is M(4, 6).
The distance formula helps us find the distance between two points in a coordinate plane. By using the formula, students can determine the length of a line segment or the distance between any two arbitrary points. The answer key provides a clear explanation of each step involved in applying the distance formula.
Example:
- Problem: Find the distance between the points A(2, 4) and B(6, 8).
- Solution:
- Let’s label the x-coordinates of the points as x1 and x2, and the y-coordinates as y1 and y2.
- Plug the values into the distance formula: d = √((x2 – x1)2 + (y2 – y1)2).
- Calculate the distance: d = √((6 – 2)2 + (8 – 4)2) = √(16 + 16) = √32.
- Therefore, the distance between the points A(2, 4) and B(6, 8) is √32 units.
The answer key provides a comprehensive guide to understanding and applying the midpoint and distance formulas, allowing students to gain confidence in their problem-solving abilities and develop a solid foundation in geometry and algebra.
Explaining the Midpoint Formula
The midpoint formula is a mathematical equation used to find the midpoint between two given points on a coordinate plane. It is extremely useful in various fields such as geometry, physics, and engineering. The formula itself is quite simple and straightforward, making it easy to calculate the midpoint.
Let’s consider two points, (x1, y1) and (x2, y2), on a coordinate plane. The midpoint formula states that the coordinates of the midpoint (x, y) are obtained by averaging the corresponding x-values and y-values of the two points. In other words, the x-coordinate of the midpoint is the average of the x-coordinates of the given points, and the y-coordinate of the midpoint is the average of the y-coordinates of the given points.
Mathematically, the formula can be represented as:
x = (x1 + x2) / 2
y = (y1 + y2) / 2
For example, let’s say we have two points: A(2, 4) and B(6, 8). To find the midpoint between these two points, we can plug in the values into the formula:
x = (2 + 6) / 2 = 4
y = (4 + 8) / 2 = 6
The midpoint between A and B is (4, 6). This means that if we draw a straight line connecting points A and B, the midpoint will be located exactly at the center of that line.
The midpoint formula is not only useful for finding the exact midpoint between two points but also for solving various geometric problems, such as finding the center of a circle or the midpoint of a line segment. It provides a simple and efficient way to calculate these values and is an essential tool in many mathematical and scientific applications.
Solving Problems with the Midpoint Formula

The midpoint formula is a useful tool in solving problems that involve finding the midpoint between two given points on a coordinate plane. By finding the coordinates of the midpoint, we can determine the exact point that lies equidistant from both points. This formula can be applied to a range of scenarios, from simple geometric shapes to real-world applications.
When solving problems with the midpoint formula, it is important to remember the formula itself, which states that the midpoint is the average of the x-coordinates and the y-coordinates of the given points. This can be represented as:
Midpoint = (x1 + x2) / 2 , (y1 + y2) / 2
Once we have the midpoint coordinates, we can use them to solve various types of problems. For example, in geometry, we can determine the endpoints of a line segment when given the midpoint and one endpoint. By using the midpoint formula, we can find the coordinates of the other endpoint by doubling the x-coordinate and the y-coordinate of the midpoint, and subtracting the coordinates of the given endpoint. This allows us to find the exact location of the missing endpoint and complete the line segment.
In real-world applications, the midpoint formula can be used to solve problems involving distance and time. For instance, if we know the coordinates of two cities on a map and want to find the midpoint between them, we can use the formula to determine the exact location of a halfway point. This can be helpful in terms of calculating the distance between two places or planning a route for travel.
In summary, the midpoint formula is a valuable tool for solving problems that involve finding the midpoint between two given points. By understanding and applying the formula, we can determine the coordinates of the midpoint and use this information to solve a variety of geometric and real-life problems.
Understanding the Distance Formula
The distance formula is a mathematical equation used to determine the distance between two points in a coordinate plane. It is derived from the Pythagorean theorem and is applicable in both two and three-dimensional spaces.
The formula is as follows: d = √((x2 – x1)^2 + (y2 – y1)^2)
Let’s break down the formula step by step to understand how it works. The coordinates of the two points are represented as (x1, y1) and (x2, y2). To find the distance between these two points, we start by subtracting the x-coordinates and squaring the result. We do the same for the y-coordinates. Then, we add the squared results together. Finally, we take the square root of the sum to obtain the distance.
This formula can be incredibly useful in various real-life applications. For example, it can be used to calculate the length of a line segment, the distance between two cities on a map, or the distance traveled by an object in space. Additionally, it is often used in geometry and physics to solve problems involving coordinate planes.
In conclusion, the distance formula is a powerful tool for determining the distance between two points in a coordinate plane. By understanding the equation and its derivation, we can apply it to solve a wide range of mathematical and real-world problems.
Applying the Distance Formula in Real-life Situations
The distance formula is a mathematical tool that allows us to calculate the distance between two points in a coordinate plane. While it may seem like an abstract concept, the distance formula has many practical applications in real-life situations. Understanding and applying the distance formula can help us solve various problems and make informed decisions.
One real-life situation where the distance formula is applicable is in navigation. Suppose you are planning a road trip and want to determine the shortest route between two cities. By using the distance formula, you can calculate the straight-line distance between the two cities and choose the most efficient path. This can save you time and fuel, ensuring a smoother and more cost-effective journey.
Another practical application of the distance formula is in sports. For example, in baseball, the distance between the pitcher’s mound and home plate is crucial. By using the distance formula, coaches and players can calculate the exact distance and adjust their strategy accordingly. Similarly, in track and field events, such as the long jump or javelin throw, understanding the distance formula allows athletes to accurately measure and improve their performance.
Common Mistakes to Avoid when Using the Midpoint and Distance Formula
When working with the midpoint and distance formula in mathematics, it is important to be aware of common mistakes that can easily be made. These formulas are used to find the midpoint or distance between two points on a coordinate plane, and accuracy is key to obtaining correct results.
One common mistake is incorrectly identifying the coordinates of the given points. Ensure that you accurately read and interpret the coordinates provided. Mixing up the x and y values can lead to significant errors in your calculations.
Another common mistake is forgetting to square absolute values when calculating distances. The distance formula requires finding the square root of the sum of the squared differences in the x and y coordinates. Failing to square the absolute values will result in incorrect distances.
It is also important to properly apply the midpoint formula when finding the midpoint between two points. The midpoint formula involves finding the average of the x coordinates and the average of the y coordinates of the given points. Mistakes in this calculation can lead to incorrect midpoints.
Additionally, avoid rounding values too early in your calculations. Rounding prematurely can introduce rounding errors that accumulate and affect the accuracy of your final answer. It is best to keep calculations in their exact form until the final step.
To prevent errors, double-check your work at each step and use clear organization to keep track of calculations. Take the time to carefully review your answers to ensure they make sense in the context of the problem. By avoiding these common mistakes, you can confidently and accurately use the midpoint and distance formula in your mathematics studies and applications.
Practice Problems and Answer Key
Below are some practice problems that will help you reinforce your understanding of the midpoint and distance formula. Try to solve them on your own before checking the answer key provided below.
- Find the midpoint between the points A(2, 4) and B(6, 8).
- Find the distance between the points C(3, 7) and D(9, 1).
- Find the coordinates of the midpoint between the points E(-5, -2) and F(-1, 8).
- Find the distance between the points G(-2, 5) and H(4, -3).
Answer Key
- The midpoint between A(2, 4) and B(6, 8) is M(4, 6).
- The distance between C(3, 7) and D(9, 1) is 10 units.
- The midpoint between E(-5, -2) and F(-1, 8) is M(-3, 3).
- The distance between G(-2, 5) and H(4, -3) is approximately 10.2 units.
These practice problems and their solutions should help solidify your understanding of the midpoint and distance formula. Remember to always double-check your calculations and verify your answers to ensure accuracy. Keep practicing and soon you’ll be a pro at using these formulas!