Master the Pythagorean Theorem: Downloadable PDF Test Questions and Detailed Answers

Pythagorean theorem test questions and answers pdf

Are you studying the Pythagorean Theorem and need some practice questions to test your understanding? Look no further! In this article, we have compiled a collection of Pythagorean Theorem test questions and answers in PDF format, perfect for studying on the go or printing out for classroom use.

The Pythagorean Theorem is a fundamental concept in geometry that states that in a right-angled triangle, the square of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the other two sides. Understanding and applying this theorem is crucial for solving various problems and calculations involving right triangles, such as finding unknown side lengths or determining whether a triangle is right-angled or not.

Our PDF contains a variety of test questions that cover different aspects of the Pythagorean Theorem. These questions range in difficulty, allowing you to gradually build your skills and confidence. Each question is accompanied by a detailed solution, which will help you understand the steps involved in finding the correct answer. Whether you’re a student, teacher, or enthusiast, our Pythagorean Theorem test questions and answers PDF is a valuable resource for honing your geometry skills.

What is the Pythagorean theorem?

The Pythagorean theorem is a fundamental concept in geometry that relates to the relationship between the sides of a right triangle. It states that in a right triangle, the square of the length of the hypotenuse is equal to the sum of the squares of the lengths of the other two sides.

This theorem is named after the ancient Greek mathematician Pythagoras, who is credited with its discovery. The Pythagorean theorem is often written as a mathematical equation: a^2 + b^2 = c^2, where a and b represent the lengths of the two legs of the triangle, and c represents the length of the hypotenuse.

For example, if we have a right triangle with one leg measuring 3 units and another leg measuring 4 units, we can use the Pythagorean theorem to calculate the length of the hypotenuse. Substituting these values into the equation, we have: 3^2 + 4^2 = c^2. Solving for c, we find that the length of the hypotenuse is 5 units.

The Pythagorean theorem is not only important in mathematics, but it also has many practical applications in other fields such as engineering and physics. It allows us to calculate distances, determine angles, and solve various real-world problems involving right triangles.

Explanation of the Pythagorean Theorem and its Application in Geometry

The Pythagorean theorem is a fundamental principle in geometry that relates the lengths of the sides of a right triangle. It states that in a right triangle, the square of the length of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the lengths of the other two sides.

The theorem can be stated using the formula: a² + b² = c², where ‘a’ and ‘b’ represent the lengths of the two legs of the right triangle, and ‘c’ represents the length of the hypotenuse.

This theorem has numerous applications in geometry. One of its key applications is in finding the length of an unknown side of a right triangle, given the lengths of the other two sides. This is particularly useful when we have a right triangle but do not know the length of one of its sides.

The Pythagorean theorem can also be used to determine if a triangle is a right triangle. By comparing the squares of the lengths of the sides, we can determine if the sum of the squares of the two shorter sides is equal to the square of the longest side. If it is, then the triangle satisfies the Pythagorean theorem and is a right triangle.

In addition to applications in triangle calculations, the Pythagorean theorem is also used to solve problems related to distance and coordinates. It is commonly used in navigation and surveying, as well as in physics and engineering.

  • Example: A triangle has two sides of length 3 and 4 units. To find the length of the third side, we can use the Pythagorean theorem:
  • 3² + 4² = c²
  • 9 + 16 = c²
  • 25 = c²
  • c = 5 units

The Pythagorean theorem is a powerful tool in geometry that allows us to solve various problems involving right triangles and their side lengths. Its applications extend beyond geometry and are widely used in other fields as well.

How to Solve Pythagorean Theorem Problems

Solving Pythagorean theorem problems involves applying the formula a^2 + b^2 = c^2 to find the missing side length or the hypotenuse of a right triangle. To solve these problems, you need to have a clear understanding of the Pythagorean theorem and be able to identify the different sides of a right triangle.

Steps to Solve Pythagorean Theorem Problems:

Steps to Solve Pythagorean Theorem Problems:

  1. Identify the legs and hypotenuse: In a right triangle, the two sides that form the right angle are called the legs, and the side opposite the right angle is called the hypotenuse. Identify which sides are given and which side you need to find.
  2. Label the sides: Label the sides of the triangle with variables, such as ‘a’ and ‘b’ for the legs, and ‘c’ for the hypotenuse. Use the Pythagorean theorem formula a^2 + b^2 = c^2 to set up the equation based on the labeled sides.
  3. Solve the equation: Substitute the given values into the equation and solve for the unknown variable. This might involve simplifying the equation, applying the square root property, or using basic algebraic operations to isolate the variable.
  4. Check your answer and round if necessary: Once you have obtained the value for the unknown side, double-check your answer by substituting the known values back into the Pythagorean theorem equation to ensure that it satisfies the equation. Round the final answer to the appropriate number of decimal places or significant figures, if required.

By following these steps, you can successfully solve Pythagorean theorem problems and find the missing side lengths or hypotenuse of right triangles. Remember to carefully label the sides and double-check your answer to ensure accuracy.

Steps for solving Pythagorean theorem problems with examples

Steps for solving Pythagorean theorem problems with examples

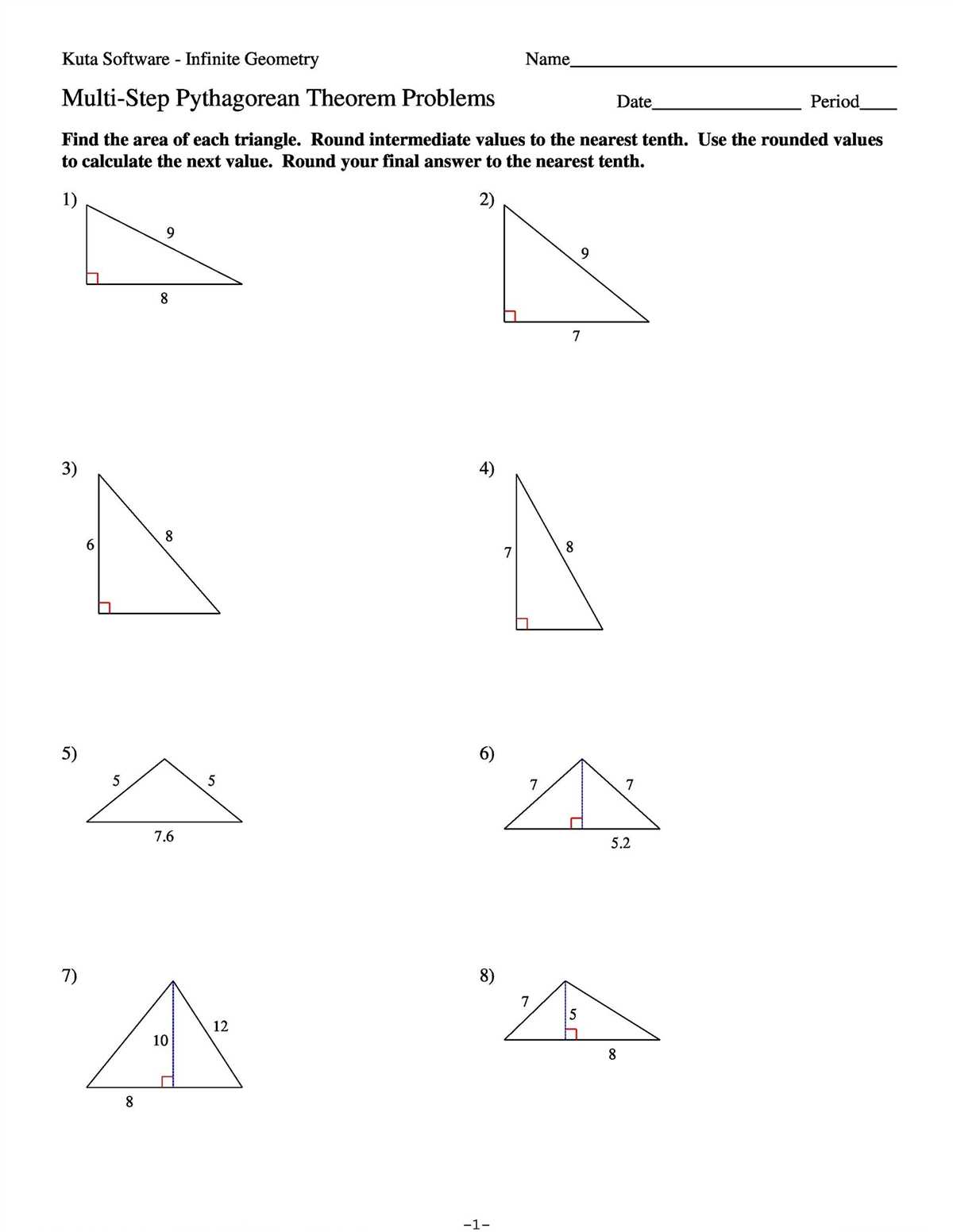
The Pythagorean theorem is a fundamental concept in geometry that allows us to calculate the length of one side of a right triangle when we know the lengths of the other two sides. To solve Pythagorean theorem problems, follow these steps:

Step 1: Identify the given information

First, determine what information is given in the problem. This may include the lengths of two sides of the triangle or the length of one side and the hypotenuse.

  • Example: In a right triangle, the length of one leg is 5 units and the length of the hypotenuse is 13 units. Find the length of the other leg.

Step 2: Use the Pythagorean theorem

The Pythagorean theorem states that in a right triangle, the square of the length of the hypotenuse is equal to the sum of the squares of the lengths of the two legs. Use this theorem to set up an equation.

  • Example: Using the Pythagorean theorem, we have a2 + b2 = c2. Substitute the given values: 52 + b2 = 132.

Step 3: Solve the equation

Now solve the equation to find the value of the unknown side length. This may involve simplifying, factoring, or using the quadratic formula.

  • Example: Simplifying the equation, we have 25 + b2 = 169. Subtract 25 from both sides: b2 = 144. Then take the square root of both sides: b = 12.

Step 4: Check your answer

Lastly, verify that your answer is correct by substituting it back into the original problem or using the Pythagorean theorem to calculate the lengths of the other sides.

  • Example: To check, substitute b = 12 back into the Pythagorean theorem: 52 + 122 = 132. Simplifying, we have 25 + 144 = 169, which is true.

By following these steps, you can confidently solve Pythagorean theorem problems and find the lengths of the sides of right triangles.

Pythagorean theorem test questions

Are you ready to put your knowledge of the Pythagorean theorem to the test? Below are some example questions that can help you practice and reinforce your understanding of this fundamental mathematical concept.

Question 1: Given a right-angled triangle with one leg of length 5 units and the other leg of length 12 units, what is the length of the hypotenuse?

Answer: To find the length of the hypotenuse, we can use the Pythagorean theorem, which states that in a right-angled triangle, the square of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the other two sides. In this case, we have:

  • Leg 1: 5 units
  • Leg 2: 12 units
  • Hypotenuse: ?

We can calculate the length of the hypotenuse as follows:

  1. Square the length of the first leg: 5^2 = 25
  2. Square the length of the second leg: 12^2 = 144
  3. Add the two squared values together: 25 + 144 = 169
  4. Finally, take the square root of the sum to find the length of the hypotenuse: √169 = 13 units

Therefore, the length of the hypotenuse in this right-angled triangle is 13 units.

Question 2: In a right-angled triangle, if one leg is 8 units and the hypotenuse is 17 units, what is the length of the other leg?

Answer: Let’s call the length of the other leg “x”. Using the Pythagorean theorem, we can set up the following equation:

x^2 + 8^2 = 17^2

Simplifying the equation, we have:

x^2 + 64 = 289

Subtracting 64 from both sides of the equation, we get:

x^2 = 225

Taking the square root of both sides, we find:

x = 15

Therefore, the length of the other leg is 15 units.

These are just a couple of examples of the types of questions you may encounter when testing your knowledge of the Pythagorean theorem. Remember to understand the theorem itself and be proficient in applying it to solve various problems involving right-angled triangles.

Collection of Multiple-Choice and Problem-Solving Questions Related to the Pythagorean Theorem

The Pythagorean theorem is a fundamental concept in geometry that states that in a right-angled triangle, the square of the length of the hypotenuse is equal to the sum of the squares of the lengths of the other two sides. As such, it has numerous applications in solving real-world problems and is an important topic in mathematics education.

Here is a collection of multiple-choice and problem-solving questions that will help test your understanding of the Pythagorean theorem:

Multiple-Choice Questions:

  1. Question: In a right-angled triangle with side lengths of 3 and 4 units, what is the length of the hypotenuse?
    • a) 5 units
    • b) 6 units
    • c) 7 units
    • d) 8 units
  2. Question: If the lengths of the two shorter sides of a right-angled triangle are 5 and 12 units, what is the length of the hypotenuse?
    • a) 13 units
    • b) 14 units
    • c) 15 units
    • d) 16 units

Problem-Solving Questions:

Problem-Solving Questions:

1. A ladder is leaning against a wall. The angle between the ladder and the ground is 60 degrees, and the ladder is 10 meters long. How far is the base of the ladder from the wall?

2. A flagpole is standing on level ground. A person standing 20 meters away from the base of the flagpole measures the angle of elevation to the top of the flagpole as 45 degrees. How tall is the flagpole?

3. A rectangular field has dimensions of 6 meters by 8 meters. A diagonal line is drawn from one corner to the opposite corner. What is the length of the diagonal?

4. Two roads meet at a right angle. Road A is 5 kilometers long, and road B is 12 kilometers long. What is the shortest distance between the two roads?

These questions cover various scenarios where the Pythagorean theorem can be applied to find unknown lengths or distances. Solving them will help reinforce your understanding of the theorem and its applications.

Pythagorean Theorem Test Answers

The Pythagorean Theorem is a fundamental concept in geometry that deals with right triangles. It states that in a right triangle, the square of the length of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the lengths of the other two sides.

When it comes to taking a Pythagorean Theorem test, it is important to understand the theorem itself and its applications. Here are some common questions you might encounter on a Pythagorean Theorem test, along with their answers:

1. Find the length of the hypotenuse:

1. Find the length of the hypotenuse:

To find the length of the hypotenuse, we need to use the Pythagorean Theorem. Let’s say the lengths of the other two sides are a and b. Then, the length of the hypotenuse, c, can be found using the formula c = √(a^2 + b^2).

2. Determine if a triangle is a right triangle:

2. Determine if a triangle is a right triangle:

To determine if a triangle is a right triangle, we can use the Pythagorean Theorem. If the square of the length of the longest side (hypotenuse) is equal to the sum of the squares of the other two sides, then the triangle is a right triangle.

3. Solve for the missing side length:

Given a right triangle with known side lengths, we can use the Pythagorean Theorem to solve for the missing side length. For example, if we know the lengths of the two legs, we can find the length of the hypotenuse by rearranging the formula to solve for c. Similarly, if we know the length of the hypotenuse and one of the legs, we can solve for the length of the other leg.

  • Example: Find the length of the missing side:
    • Given: One leg = 3 units, Hypotenuse = 5 units
    • Solution: Using the formula c = √(a^2 + b^2), we can solve for the other leg as follows:
      1. c = √(a^2 + b^2)
      2. 5 = √(3^2 + b^2)
      3. 5 = √(9 + b^2)
      4. 25 = 9 + b^2
      5. b^2 = 16
      6. b = 4

      Therefore, the length of the missing side is 4 units.

Correct answers and explanations for the Pythagorean theorem test questions

In this section, we will provide the correct answers and explanations for the Pythagorean theorem test questions presented earlier. Let’s recap the questions:

  1. Question 1: If the lengths of two sides of a right triangle are 3 cm and 4 cm, what is the length of the hypotenuse?

  2. Question 2: A ladder is leaning against a wall. The base of the ladder is 6 meters away from the wall while the top of the ladder reaches a height of 8 meters. What is the length of the ladder?

  3. Question 3: The lengths of two sides of a right triangle are 5 cm and 12 cm. What is the length of the hypotenuse?

Now, let’s provide the correct answers and explanations:

  1. Question 1: The lengths of the two sides of the right triangle are given as 3 cm and 4 cm. Using the Pythagorean theorem, we can find the length of the hypotenuse (c) using the equation c^2 = a^2 + b^2. Substituting the given values, we have c^2 = 3^2 + 4^2 = 9 + 16 = 25. Taking the square root of both sides, we get c = √25 = 5 cm. Therefore, the length of the hypotenuse is 5 cm.

  2. Question 2: The base of the ladder is given as 6 meters and the height reached by the ladder is 8 meters. We can consider the ladder, the wall, and the ground as the three sides of a right triangle. The base is one of the sides, the height is the other side, and the ladder is the hypotenuse. Using the Pythagorean theorem, we can find the length of the ladder (c) using the equation c^2 = a^2 + b^2. Substituting the given values, we have c^2 = 6^2 + 8^2 = 36 + 64 = 100. Taking the square root of both sides, we get c = √100 = 10 meters. Therefore, the length of the ladder is 10 meters.

  3. Question 3: The lengths of the two sides of the right triangle are given as 5 cm and 12 cm. Using the Pythagorean theorem, we can find the length of the hypotenuse (c) using the equation c^2 = a^2 + b^2. Substituting the given values, we have c^2 = 5^2 + 12^2 = 25 + 144 = 169. Taking the square root of both sides, we get c = √169 = 13 cm. Therefore, the length of the hypotenuse is 13 cm.

In conclusion, the correct answers for the Pythagorean theorem test questions are:

  1. The length of the hypotenuse is 5 cm.
  2. The length of the ladder is 10 meters.
  3. The length of the hypotenuse is 13 cm.

These answers were obtained by applying the Pythagorean theorem, which states that in a right triangle, the square of the length of the hypotenuse is equal to the sum of the squares of the lengths of the other two sides.