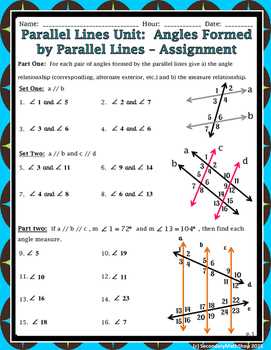
In geometry, the concept of parallel lines is fundamental. Parallel lines are two lines in a plane that never intersect, no matter how far they are extended. Proving that lines are parallel can be done using various methods and theorems. In this article, we will explore the answer key to the topic “4.3 Proving Lines are Parallel”.
To prove that lines are parallel, we need to establish certain conditions or criteria. One common method is the use of corresponding angles. If two lines are intersected by a transversal and the corresponding angles are congruent, then the lines are parallel. This method is known as the Corresponding Angles Postulate. It provides a simple and effective way of proving lines are parallel.
Another method is the use of alternate interior angles. If two lines are intersected by a transversal and the alternate interior angles are congruent, then the lines are parallel. This method is known as the Alternate Interior Angles Theorem. It is based on the idea that if two lines are cut by a transversal, and the alternate interior angles are congruent, then the lines are parallel.
Furthermore, the use of consecutive interior angles can also be employed to prove lines are parallel. If two lines are intersected by a transversal and the consecutive interior angles are supplementary, then the lines are parallel. This method is known as the Consecutive Interior Angles Theorem. It provides yet another effective way of proving lines are parallel.
In conclusion, proving lines are parallel is an important concept in geometry. By using methods such as corresponding angles, alternate interior angles, and consecutive interior angles, we can confidently establish whether lines are parallel or not. Understanding and applying these theorems is crucial for solving various geometric problems and proofs.
Proving Lines are Parallel: Answer Key

In geometry, proving that lines are parallel is an essential skill. Parallel lines are lines that never intersect, and identifying parallel lines helps us understand shapes and angles.
One way to prove that lines are parallel is by using the Alternate Interior Angles Theorem. According to this theorem, if two lines are cut by a transversal, and the alternate interior angles are congruent, then the lines are parallel. This theorem is based on the fact that alternate interior angles are formed on opposite sides of the transversal and have the same measure.
An example of using the Alternate Interior Angles Theorem to prove lines are parallel is as follows:
- Given: Line AB and line CD are cut by transversal EF.
- Prove: AB || CD.
To prove this, we need to show that the alternate interior angles are congruent. Let’s label the angles: angle 1, angle 2, angle 3, and angle 4. We can see that angle 1 and angle 3 are alternate interior angles and angle 2 and angle 4 are also alternate interior angles.
| Statement | Reason |
|---|---|
| 1. angle 1 ≅ angle 3 | Given |
| 2. angle 2 ≅ angle 4 | Given |
| 3. ∠1 ≅ ∠2 | Alternate Interior Angles Theorem |
| 4. ∠3 ≅ ∠4 | Alternate Interior Angles Theorem |
| 5. AB || CD | Corresponding Angles Converse |
After proving that angle 1 is congruent to angle 3 and angle 2 is congruent to angle 4, we can conclude that angles 1 and 2 are congruent, and angles 3 and 4 are congruent. Therefore, line AB is parallel to line CD.
By using the Alternate Interior Angles Theorem and other angle relationships, we can confidently prove when lines are parallel, providing a solid answer key for geometric proofs.
Understanding Parallel Lines
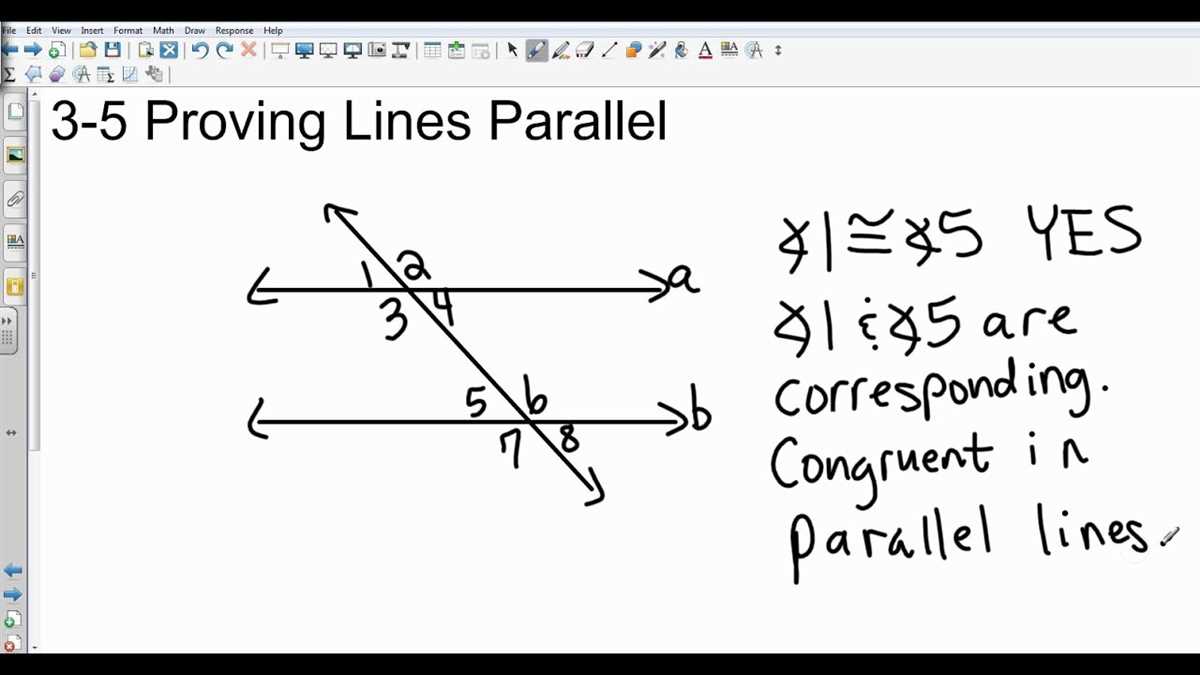
Parallel lines play an important role in geometry and have several unique properties. To understand parallel lines, it is essential to know the definition. Two lines are said to be parallel if they lie in the same plane and do not intersect, no matter how far they are extended. This definition forms the basis for proving lines are parallel in various geometric situations.
One way to prove that lines are parallel is by using the Alternate Interior Angles Theorem. According to this theorem, if two parallel lines are intersected by a transversal, then the alternate interior angles formed are congruent. This means that if the measure of one alternate interior angle is known, it can be concluded that the corresponding alternate interior angle is also congruent. By using this theorem and measuring the angles formed, it is possible to provide evidence for the parallelity of lines.
Another method to prove lines are parallel is by using the Converse of the Corresponding Angles Postulate. This postulate states that if two lines are intersected by a transversal and the corresponding angles are congruent, then the lines are parallel. This means that if the corresponding angles of intersected lines are congruent, it can be concluded that the lines themselves are parallel. This proof method relies on the idea that congruent corresponding angles are a characteristic property of parallel lines.
In addition to these theorems, there are other methods and strategies to prove lines are parallel. Some of these include the Consecutive Interior Angles Theorem, the Triangle Angle Sum Theorem, and the Contradiction Proof. Each proof method utilizes different properties and theorems to provide evidence for parallel lines. Understanding these proof techniques is essential for solving geometry problems involving parallel lines.
Definition of Corresponding Angles
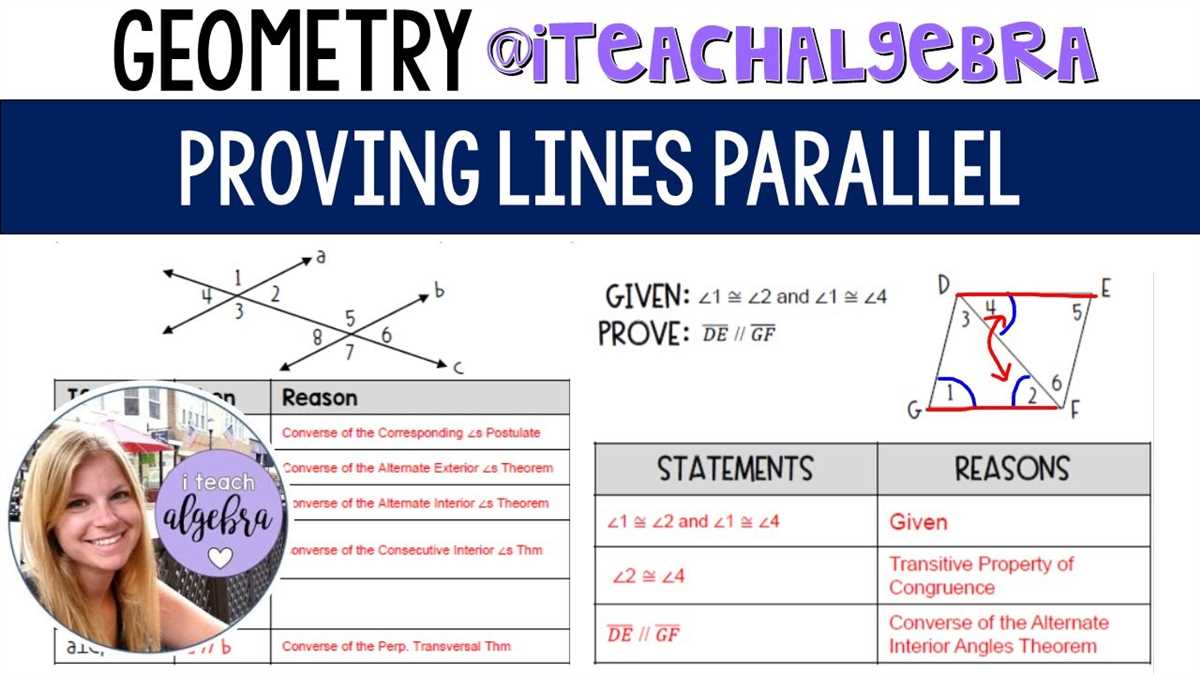
In geometry, corresponding angles are a pair of angles formed by two parallel lines and a transversal. When two lines are parallel, they never intersect and are always the same distance apart. A transversal is a line that intersects two or more other lines at different points. When a transversal intersects a pair of parallel lines, it forms eight angles.
Corresponding angles are positioned in the same relative position at each intersection created by the transversal and the parallel lines. In other words, corresponding angles are formed in the same location at each intersection. The pairs of corresponding angles are located on the same side of the transversal and are congruent. Congruent angles have the same measure, so each pair of corresponding angles has the same angle measurement.
Key Phrases:
- Corresponding angles
- Parallel lines
- Transversal
- Intersection
- Relative position
- Same side
- Congruent angles
Understanding the concept of corresponding angles is important in the study of geometry. It allows us to identify relationships and make predictions about the measures of angles formed by parallel lines and a transversal. By recognizing corresponding angles, we can use them as a basis for proving various geometric theorems and solving problems related to parallel lines and angles.
Overall, the definition of corresponding angles provides a fundamental understanding of the relationships between angles formed by parallel lines and a transversal. It allows us to analyze and manipulate angles in geometric proofs and problem-solving situations. By recognizing the properties and characteristics of corresponding angles, we can further explore the intricate connections within the world of geometry.
Alternate Interior and Exterior Angles
The concept of alternate interior and exterior angles is an important aspect of parallel lines and their properties. When two parallel lines are intersected by a transversal, alternate interior angles are the angles that are formed on the inside of the parallel lines and on opposite sides of the transversal. Similarly, alternate exterior angles are the angles formed on the outside of the parallel lines and on opposite sides of the transversal.
Alternate interior angles are congruent, which means they have the same measure. This property holds true for any pair of parallel lines intersected by a transversal. The alternate exterior angles are also congruent. This can be proved using various geometric theorems and postulates.
Recognizing alternate interior and exterior angles is useful in proving the congruency or parallelism of lines. If two lines are known to be parallel and intersected by a transversal, the congruency of alternate interior angles or alternate exterior angles can be used to show the congruency of other angles or to prove other geometric properties.
Alternate interior and exterior angles are commonly used in various applications of geometry, such as in the construction of buildings, in engineering designs, and in solving real-world problems involving parallel lines. They provide a fundamental understanding of the relationships between angles formed by intersecting lines and play a crucial role in geometric reasoning.
Applying the Parallel Lines Theorem
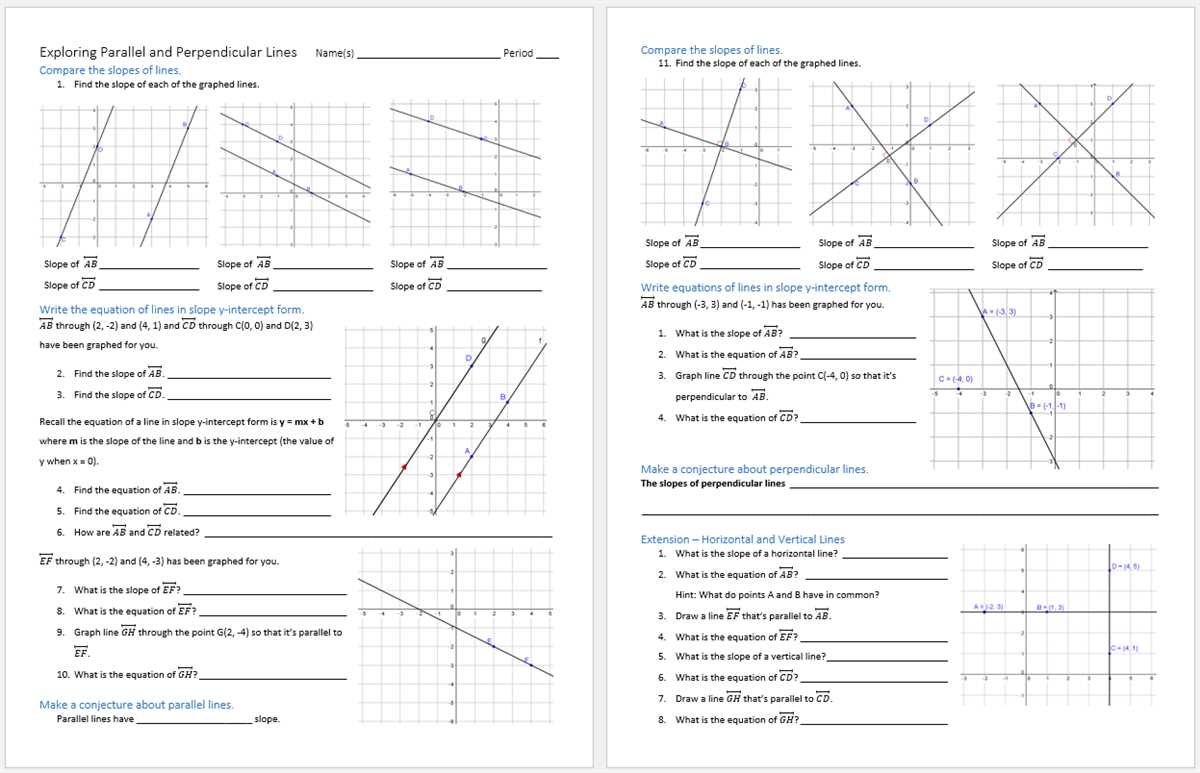
The Parallel Lines Theorem states that if two lines are cut by a transversal and the corresponding angles are congruent, then the lines are parallel. This theorem provides a powerful tool for proving that certain lines are parallel. By identifying congruent corresponding angles, we can conclude that the lines are parallel without having to show any other information about the lines or angles.
When applying the Parallel Lines Theorem, it is important to carefully examine the given information and look for congruent corresponding angles. These angles may be formed by a transversal intersecting two parallel lines, or they may be given as congruent in the problem. By identifying these angles and applying the theorem, we can quickly determine whether the lines are parallel or not.
In order to prove that lines are parallel using the Parallel Lines Theorem, it is helpful to list the corresponding angles that are given as congruent. By organizing the angles in a table or list, we can easily see which angles are congruent and make a conclusion about the parallelism of the lines. It may also be helpful to draw a diagram to visually represent the given information and aid in the identification of congruent corresponding angles.
In conclusion, the Parallel Lines Theorem is a valuable tool for proving that lines are parallel. By identifying congruent corresponding angles, we can quickly and efficiently determine whether the lines are parallel or not. Organizing the given information and drawing a diagram can aid in the application of the theorem and make the process of proving parallelism easier. By mastering the use of the Parallel Lines Theorem, mathematicians can confidently prove parallelism in a variety of geometric situations.
Using the Midline Theorem
In geometry, the Midline Theorem is a useful tool for proving that certain lines are parallel. It states that if a line is drawn parallel to one side of a triangle, then it divides the other two sides proportionally.
By using the Midline Theorem, we can determine whether two lines are parallel without measuring angles or using any other complicated methods. All we need to do is find a line that is parallel to one side of the given figure, and then show that it divides the other two sides proportionally.
Here is a step-by-step process for using the Midline Theorem to prove parallel lines:
- Identify the line that is parallel to one side of the given figure.
- Show that the line divides the other two sides proportionally.
- If the line divides the other two sides proportionally, then the two given lines are parallel.
By following these steps, we can confidently prove that two lines are parallel using the Midline Theorem. This theorem provides a straightforward and efficient method for proving parallel lines, saving us time and effort in geometry proofs.
Overall, the Midline Theorem is a powerful tool in geometry that allows us to easily determine whether two lines are parallel. By understanding and applying this theorem, we can simplify our proofs and confidently solve geometric problems.