Trigonometry is a branch of mathematics that deals with the relationships between the angles and sides of triangles. One important concept in trigonometry is the right triangle, which has one angle equal to 90 degrees. Right triangle trigonometry involves using the ratios of the lengths of the sides of a right triangle to solve for unknown angles or sides.
In this unit test, we will focus on Part 1 of right triangle trigonometry, which includes the basic trigonometric ratios: sine, cosine, and tangent. These ratios are defined as the ratios of the lengths of certain sides of a right triangle.
To better understand these ratios, we will explore how they are calculated and the relationships between them. We will also learn how to use these ratios to solve for missing side lengths and angle measures in right triangles.
Throughout this unit test, we will work through various examples and practice problems to solidify our understanding of right triangle trigonometry. By the end of this test, we will have a strong foundation in Part 1 of right triangle trigonometry and be prepared to move on to more advanced concepts in Part 2.
Right Triangle Trigonometry: Unit Test – Part 1
In mathematics, trigonometry is a branch that deals with the relationships between the angles and sides of triangles. Specifically, it focuses on right triangles, which have one angle measuring 90 degrees. Trigonometry plays a crucial role in various fields, including physics, engineering, and navigation.
The unit test on Right Triangle Trigonometry, Part 1, is designed to assess your understanding of the fundamental concepts and formulas related to trigonometric functions. This test will evaluate your ability to solve problems involving angle measures, side lengths, and the three primary trigonometric ratios: sine, cosine, and tangent.
The test will cover the following topics:
- Definition and calculation of sine, cosine, and tangent
- Calculating angles using inverse trigonometric functions
- Using the Pythagorean Theorem to find missing side lengths
- Applying trigonometric functions to solve real-life problems
To prepare for the unit test, make sure you have a good understanding of the trigonometric functions and their properties. Review the definitions, formulas, and key concepts covered in class or your textbook. Practice solving various types of problems, including those involving right triangles and trigonometric ratios.
Remember to show your work and provide clear explanations when answering test questions. This will help ensure that you receive full credit for your responses. Good luck!
Overview
This unit test is designed to assess your understanding of right triangle trigonometry. Trigonometry is a branch of mathematics that deals with the relationships between the angles and sides of triangles. In right triangle trigonometry, we specifically focus on the angles and sides of right triangles.
In this unit test, you will be tested on your ability to solve various problems related to right triangle trigonometry. You will need to apply the definitions, formulas, and ratios of trigonometric functions such as sine, cosine, and tangent to solve these problems.
You will also need to know how to use the Pythagorean theorem to find the lengths of the sides of right triangles. The Pythagorean theorem states that in a right triangle, the square of the length of the hypotenuse is equal to the sum of the squares of the lengths of the other two sides.
Throughout this unit test, you will encounter different types of problems, such as finding missing angles or sides of right triangles, using trigonometric ratios to solve for unknown values, and applying the Pythagorean theorem to find missing side lengths.
It is important to review the concepts, formulas, and problem-solving techniques covered in the lessons before attempting this unit test. Make sure you have a solid understanding of the definitions and applications of trigonometric functions, as well as the Pythagorean theorem.
Definition of Right Triangle
A right triangle is a geometric shape that consists of three sides and three angles. It is called a “right” triangle because it has one angle that measures exactly 90 degrees, which is referred to as the right angle. The other two angles are acute angles, meaning they are less than 90 degrees.
In a right triangle, the side opposite the right angle is called the hypotenuse. The other two sides are known as the legs. The length of the hypotenuse is always the longest side in the triangle, while the lengths of the legs can vary.
Pythagorean Theorem: The Pythagorean theorem is a fundamental principle in right triangle trigonometry. It states that in a right triangle, the sum of the squares of the lengths of the two legs is equal to the square of the length of the hypotenuse. This theorem can be represented by the equation a^2 + b^2 = c^2, where a and b are the lengths of the legs, and c is the length of the hypotenuse.
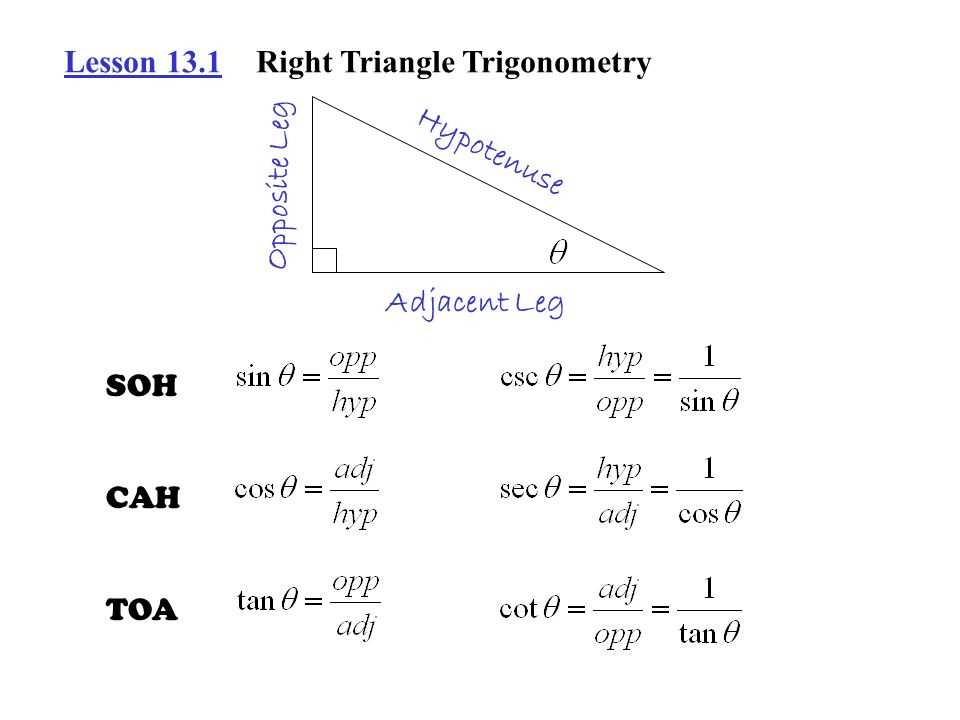
Right Triangle Trigonometric Ratios:
In addition to the Pythagorean theorem, right triangle trigonometry involves the use of trigonometric ratios. The three primary trigonometric ratios used in right triangles are sine, cosine, and tangent.
- Sine: The sine of an angle in a right triangle is equal to the ratio of the length of the side opposite the angle to the length of the hypotenuse.
- Cosine: The cosine of an angle in a right triangle is equal to the ratio of the length of the side adjacent to the angle to the length of the hypotenuse.
- Tangent: The tangent of an angle in a right triangle is equal to the ratio of the length of the side opposite the angle to the length of the side adjacent to the angle.
These trigonometric ratios can be used to solve various problems involving right triangles, such as finding the lengths of unknown sides or determining the measures of unknown angles.
Trigonometric Ratios
The study of trigonometry involves understanding the relationships between the sides and angles of triangles. Trigonometric ratios are mathematical equations that express these relationships. These ratios are used to solve various problems involving triangles, such as finding missing sides or angles.
In a right triangle, which is a triangle with one angle measuring 90 degrees, there are three primary trigonometric ratios: sine, cosine, and tangent. These ratios are abbreviated as sin, cos, and tan, respectively. Each ratio is defined by the ratio of two sides of the triangle.
- Sine (sin): The ratio of the length of the side opposite the angle to the length of the hypotenuse.
- Cosine (cos): The ratio of the length of the side adjacent to the angle to the length of the hypotenuse.
- Tangent (tan): The ratio of the length of the side opposite the angle to the length of the side adjacent to the angle.
To calculate these ratios, it is important to label the sides of the triangle correctly. The hypotenuse is always the longest side and is opposite the right angle. The side adjacent to the angle is the one that touches the angle but is not the hypotenuse, while the side opposite the angle is the remaining side.
Trigonometric ratios are extremely useful in various fields of science, engineering, and mathematics, as they provide a way to determine unknown sides or angles in triangles. They are also used in navigation, physics, astronomy, and many other disciplines that deal with angles and distances.
Solving for Missing Sides
Let’s consider an example. Suppose we have a right triangle with one known side length and one known angle measure. To find the length of the missing side, we can use the sine ratio. The sine of an angle in a right triangle is defined as the ratio of the length of the opposite side to the length of the hypotenuse. So, if we know the length of the hypotenuse and the measure of one of the acute angles, we can use the sine ratio to find the length of the missing side.
Similarly, we can use the cosine ratio to find a missing side length if we know the length of the hypotenuse and the measure of one of the acute angles. The cosine of an angle in a right triangle is defined as the ratio of the length of the adjacent side to the length of the hypotenuse.
In some cases, we may need to find the length of a side when we only know the measure of one acute angle and the length of another side. In this situation, we can use the tangent ratio. The tangent of an angle in a right triangle is defined as the ratio of the length of the opposite side to the length of the adjacent side. So, if we know the measure of one acute angle and the length of one side, we can use the tangent ratio to find the length of the missing side.
By using the appropriate trigonometric ratios, we can solve for missing side lengths in right triangles and accurately determine the dimensions of the triangle.
Solving for Missing Angles

When working with right triangles, it is often necessary to find missing angles. There are several methods that can be used to solve for these angles, depending on the information provided in the problem.
One common method is to use the properties of complementary angles. In a right triangle, one of the angles is always 90 degrees, which means that the other two angles are complementary. For example, if one angle is given as 30 degrees, the other angle can be found by subtracting 30 from 90: 90 – 30 = 60 degrees.
Another method is to use trigonometric ratios such as sine, cosine, and tangent. These ratios relate the sides of a right triangle to the angles. For example, if the length of one of the sides and the length of the hypotenuse are known, the sine ratio can be used to find the measure of an angle. By taking the inverse sine of the ratio of the side length to the hypotenuse length, the angle can be determined.
It is important to remember that angles in a triangle always add up to 180 degrees. So, if one angle is given and another angle is found using one of the methods mentioned above, the third angle can be found by subtracting the sum of the other two angles from 180 degrees.
Overall, solving for missing angles in a right triangle requires an understanding of the properties of angles and trigonometric ratios. By applying these concepts, it is possible to determine the measures of angles that are not directly provided in the problem.
Summary
In this article, we explored the basics of right triangle trigonometry. We learned about the relationships between the sides and angles of a right triangle, and how to use trigonometric functions to solve for missing values.
We started by introducing the three primary trigonometric functions: sine, cosine, and tangent. We learned that these functions can be used to relate the ratios of the sides of a right triangle to the measure of its angles.
Next, we discussed how to use the Pythagorean theorem to determine the length of a missing side in a right triangle. This theorem states that in a right triangle, the square of the length of the hypotenuse is equal to the sum of the squares of the lengths of the other two sides.
We also explored the concept of the unit circle and how it can be used to visualize trigonometric functions. By plotting the coordinates of certain points on the unit circle, we can determine the values of sine, cosine, and tangent for specific angles.
Finally, we examined some example problems and practice exercises to reinforce our understanding of right triangle trigonometry. By applying the concepts we learned, we were able to solve for missing side lengths and angles in various right triangles.
Overall, right triangle trigonometry is a fundamental tool for understanding and solving problems involving right triangles. By mastering the concepts and techniques presented in this article, we have gained a solid foundation for further exploration of trigonometry and its applications.