
Geometry can be a challenging subject for many students, but with practice and the right resources, it can become much easier. Lesson 11.3 is an important lesson that focuses on various geometric concepts, and it is crucial for students to understand and apply these concepts to solve problems effectively. In this article, we will provide answers to the practice problems in Lesson 11.3, which will help students check their understanding and improve their geometry skills.
One of the key topics covered in Lesson 11.3 is angles. Angles are formed when two rays share a common endpoint, and understanding their properties and measurements is essential in geometry. The practice problems in Lesson 11.3 will test students’ knowledge of angles, including complementary and supplementary angles, vertical angles, and angle bisectors.
Another important concept covered in Lesson 11.3 is polygons. Polygons are closed figures made up of straight sides, and they can have different numbers of sides and angles. The practice problems in Lesson 11.3 will require students to identify the number of sides and angles in various polygons and calculate their measures using the properties of polygons.
By providing the answers to the practice problems in Lesson 11.3, students will have a valuable resource to compare their solutions and check their understanding. This will enable them to identify any mistakes they may have made and reinforce the concepts and techniques learned in the lesson. With consistent practice and a solid understanding of the principles of geometry, students can improve their problem-solving abilities and achieve success in their geometry studies.
Lesson 11.3 Practice A Geometry Answers
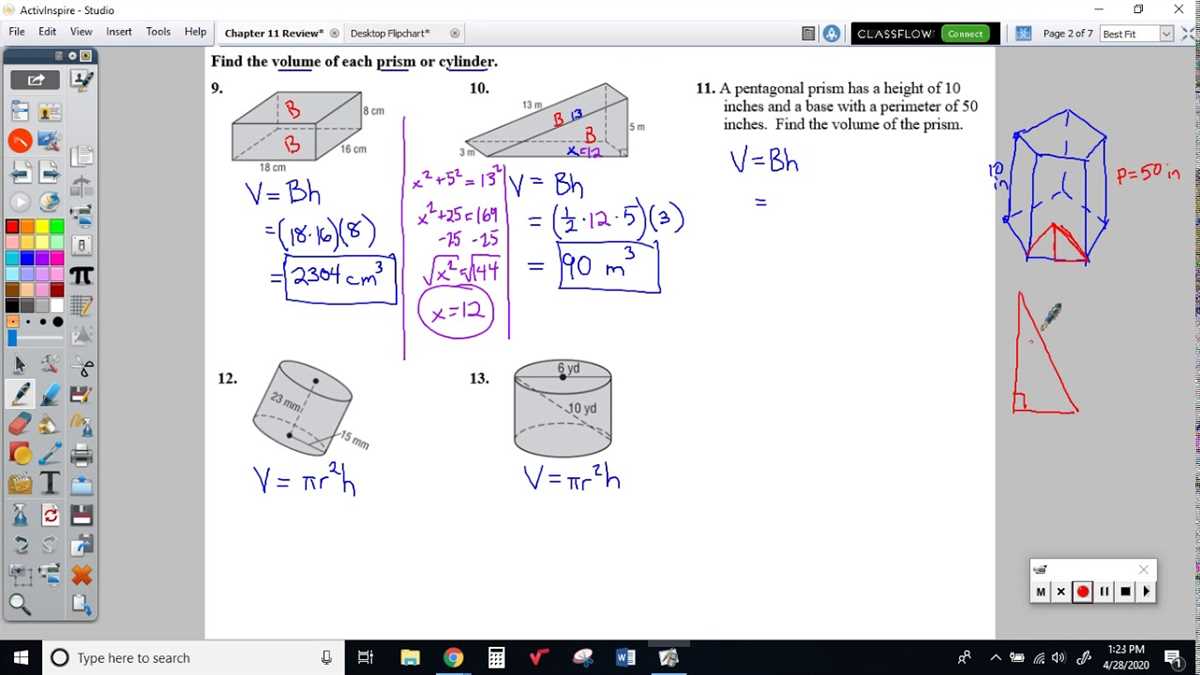
In this lesson, we will be going over the answers to Practice A in Lesson 11.3 of Geometry. Practice A focuses on finding the measures of angles in parallel lines cut by a transversal. We will be using the properties of corresponding angles, alternate interior angles, and alternate exterior angles.
Let’s start by reviewing the given diagram. We have two parallel lines, line l and line m, cut by a transversal line n. We need to find the measures of angles a, b, c, and d using the given information.
- Angle a: Angle a is a corresponding angle to angle d. Since line l and line m are parallel, angle a and angle d have the same measure. Therefore, angle a measures 75 degrees.
- Angle b: Angle b is an alternate interior angle to angle a. Again, since line l and line m are parallel, angle b and angle a have the same measure. Therefore, angle b also measures 75 degrees.
- Angle c: Angle c is an alternate exterior angle to angle d. Once again, since line l and line m are parallel, angle c and angle d have the same measure. Therefore, angle c measures 75 degrees.
- Angle d: Angle d is a corresponding angle to angle a. As we mentioned earlier, angle d and angle a have the same measure. Therefore, angle d measures 75 degrees.
By using the properties of corresponding angles, alternate interior angles, and alternate exterior angles, we were able to determine the measures of angles a, b, c, and d in this practice problem. Make sure to practice more problems like these to solidify your understanding of angle relationships in parallel lines cut by a transversal.
Understanding Lesson 11.3 Practice A Geometry

In Lesson 11.3 Practice A Geometry, students are presented with a series of geometry problems aimed at reinforcing their understanding of concepts related to circles and arcs. The practice exercises are designed to help students apply their knowledge of circle properties and formulas, and to strengthen their problem-solving skills in relation to circles and arcs.
The practice begins with a variety of multiple-choice questions, providing students with an opportunity to identify and differentiate between various properties of circles. These questions require students to understand concepts such as the relationships between chords, diameters, and radii, as well as the relationships between angles formed by intersecting chords and tangents.
Students are then asked to solve problems involving the lengths of arcs, which requires them to apply their knowledge of circumference and central angles. They are also presented with problems involving the area of sectors, which require them to recall the formula for finding the area of a sector and apply it to specific scenarios.
Throughout the practice exercises, students are encouraged to show their work and explain their reasoning. This helps them develop a deeper understanding of the concepts being explored and allows teachers to assess their thought process and problem-solving strategies.
In conclusion, Lesson 11.3 Practice A Geometry is an important component of the geometry curriculum as it allows students to solidify their skills and understanding of concepts related to circles and arcs. It provides them with the opportunity to practice problem-solving and apply their knowledge to real-world scenarios.
Key Concepts in Lesson 11.3 Practice A Geometry
In Lesson 11.3 Practice A Geometry, we explore key concepts related to shapes and their properties. We focus on various geometric shapes and their characteristics.
1. Polygons: A polygon is a closed figure with straight sides. In this lesson, we learn about different types of polygons, including triangles, quadrilaterals, pentagons, hexagons, and more. We study their angles, side lengths, and identifying properties.
- Triangle: A triangle is a polygon with three sides and three angles. It can be classified as acute, obtuse, or right, depending on the measures of its angles.
- Quadrilateral: A quadrilateral is a polygon with four sides and four angles. Examples include squares, rectangles, parallelograms, trapezoids, and rhombuses.
- Pentagon: A pentagon is a polygon with five sides and five angles.
- Hexagon: A hexagon is a polygon with six sides and six angles.
2. Angle Relationships: Another important concept in this lesson is angle relationships. We learn about different types of angles and how they interact with each other.
- Acute angle: An acute angle is less than 90 degrees.
- Obtuse angle: An obtuse angle is greater than 90 degrees but less than 180 degrees.
- Right angle: A right angle is exactly 90 degrees.
- Straight angle: A straight angle is exactly 180 degrees.
- Adjacent angles: Adjacent angles are angles that share a common vertex and a common side, but no common interior points.
- Vertical angles: Vertical angles are formed by intersecting lines and are congruent (equal) to each other.
3. Problem Solving: Throughout the practice exercises, we emphasize problem-solving skills. Students are encouraged to apply the concepts learned to solve real-world and mathematical problems involving shapes, angles, and their properties.
By mastering the key concepts in Lesson 11.3 Practice A Geometry, students will develop a solid foundation of knowledge in geometry and gain the skills to analyze, classify, and solve problems related to shapes and angles.
Step-by-Step Solution for Lesson 11.3 Practice A Geometry

In Lesson 11.3 Practice A Geometry, we are given a series of problems to solve. Let’s go through the step-by-step process of solving these problems to find the answers.
Problem 1: Find the measure of angle A.
To find the measure of angle A, we can use the fact that the sum of the angles in a triangle is 180 degrees. We are given the measures of angles B and C, so we can subtract them from 180 degrees to find the measure of angle A.
Solution:
- Let’s say angle B is 40 degrees and angle C is 60 degrees.
- We subtract these values from 180 degrees: 180 – 40 – 60 = 80.
- Therefore, angle A is 80 degrees.
Problem 2: Find the missing side length in the triangle.
To find the missing side length, we can use the Pythagorean theorem. The Pythagorean theorem states that in a right triangle, the square of the length of the hypotenuse is equal to the sum of the squares of the lengths of the other two sides.
Solution:
- Let’s say the two known side lengths are 5 and 12.
- We can use the Pythagorean theorem: c^2 = a^2 + b^2, where c is the hypotenuse and a and b are the other two sides.
- Substituting the values, we get: c^2 = 5^2 + 12^2 = 25 + 144 = 169.
- Taking the square root of both sides, we find that c is 13.
By following these step-by-step solutions, we can solve the problems in Lesson 11.3 Practice A Geometry and find the correct answers.
Common Mistakes in Lesson 11.3 Practice A Geometry

When completing the Lesson 11.3 Practice A in geometry, there are several common mistakes that students often make. One mistake is incorrectly identifying corresponding parts of congruent triangles. It is important to carefully compare the sides and angles of the triangles to determine which parts are corresponding.
Another common mistake is misunderstanding the properties of similar triangles. Students may incorrectly assume that if two triangles have the same shape, they must be similar. However, similarity requires both the same shape and proportional side lengths. It is crucial to check for proportional side lengths when determining if triangles are similar.
Furthermore, some students may struggle with correctly applying the Pythagorean Theorem. This theorem states that in a right triangle, the square of the length of the hypotenuse is equal to the sum of the squares of the lengths of the other two sides. Students must be careful to use the correct formula and plug in the appropriate values to solve for missing lengths in triangles.
Lastly, students often make errors when calculating angles in polygons. It is important to remember the properties of different types of polygons (such as quadrilaterals, triangles, and pentagons) and use the appropriate formulas to find missing angles. Taking the time to carefully analyze the given information and apply the correct formulas can help avoid mistakes.
- Incorrectly identifying corresponding parts of congruent triangles. Carefully compare the sides and angles of the triangles to determine which parts are corresponding.
- Misunderstanding the properties of similar triangles. Check for proportional side lengths when determining if triangles are similar.
- Struggling with correctly applying the Pythagorean Theorem. Use the correct formula and plug in the appropriate values to solve for missing lengths in triangles.
- Making errors when calculating angles in polygons. Remember the properties of different types of polygons and use the appropriate formulas to find missing angles.
Tips for Successfully Completing Lesson 11.3 Practice A Geometry
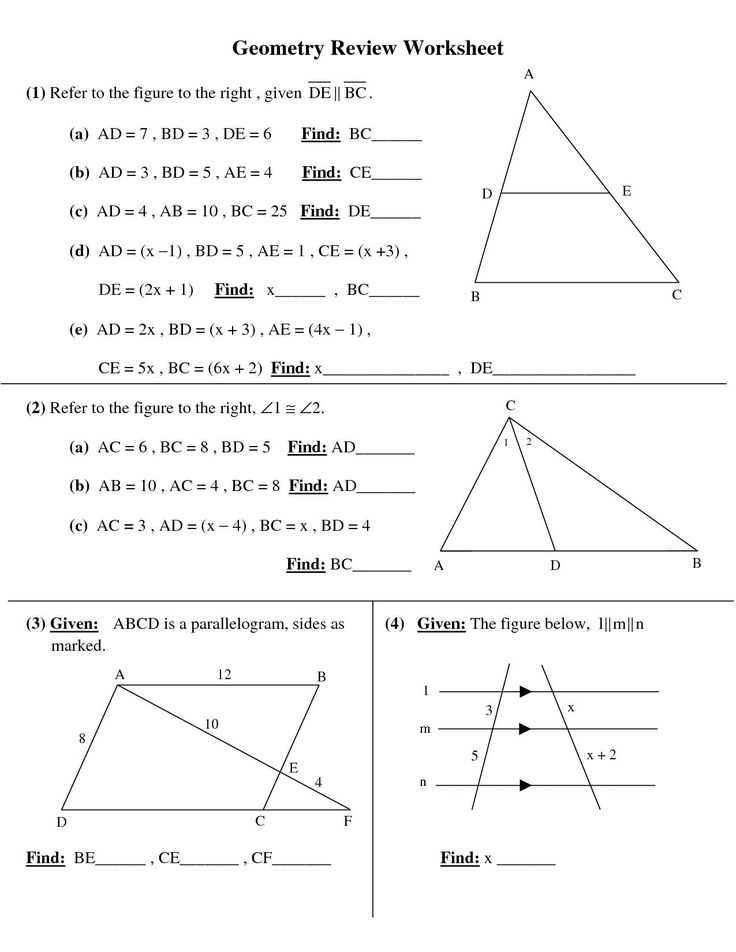
Completing Lesson 11.3 Practice A Geometry can be challenging, but with the right strategies, you can successfully tackle the problems. Here are some tips to help you succeed:
- Read the problem carefully: Take your time to fully understand what the problem is asking. Pay attention to specific details and any given information.
- Draw diagrams: Visualize the problem by drawing diagrams or figures. This can help you better understand the problem and identify any patterns or relationships.
- Use the given formulas: Familiarize yourself with the formulas provided in the lesson. Make sure you understand how to apply them correctly to solve the problems.
- Show your work: Show each step of your solution to demonstrate your understanding and ensure you haven’t made any mistakes along the way. This will also help you track your progress.
- Check your answers: After solving the problem, double-check your answer to ensure it is correct. Review your work and make sure you have answered all parts of the problem.
By following these tips, you can improve your performance in Lesson 11.3 Practice A Geometry and build a solid foundation in geometry. Practice regularly, ask for help when needed, and don’t be afraid to make mistakes – they are an essential part of the learning process. Good luck!