
A rectangular prism, also known as a rectangular cuboid, is a three-dimensional shape with six rectangular faces. It is a common shape found in everyday objects like books, boxes, and buildings. Understanding how to calculate the surface area of a rectangular prism is essential in various fields, including mathematics, engineering, and architecture.
The surface area of a rectangular prism is the total area of all its faces. To calculate it, we need to find the area of each face and then add them together. The formula for finding the surface area of a rectangular prism is:
Surface Area = 2(LW + LH + WH)
Where L represents the length, W represents the width, and H represents the height of the rectangular prism. By plugging in the dimensions into this formula, we can find the surface area. This calculation is crucial for determining the amount of material needed to build a rectangular prism or the amount of wrapping paper required to cover a gift in a rectangular box.
Surface Area of a Rectangular Prism Answer Key
Calculating the surface area of a rectangular prism can be a complex task if you are not familiar with the formula. Luckily, with the help of an answer key, you can easily find the solution. The answer key provides step-by-step instructions on how to calculate the surface area of a rectangular prism, making it easier for you to understand and apply the formula correctly.
The key begins by listing the required measurements: length, width, and height. These measurements are crucial in determining the surface area. The answer key then guides you through the process of calculating the area of each face of the rectangular prism. It highlights how to find the area of the top and bottom faces, as well as the four side faces.
Additionally, the answer key demonstrates how to add all the individual face areas together to obtain the total surface area of the rectangular prism. It emphasizes the importance of accurately adding and calculating each face to ensure an accurate final result.
The answer key also provides example problems and their corresponding solutions. These examples serve as valuable practice exercises, allowing you to strengthen your understanding of the formula and how to apply it in different scenarios. By following the instructions and examples in the answer key, you will be able to confidently calculate the surface area of any rectangular prism you encounter.
How to Calculate the Surface Area of a Rectangular Prism: Step-by-Step Guide
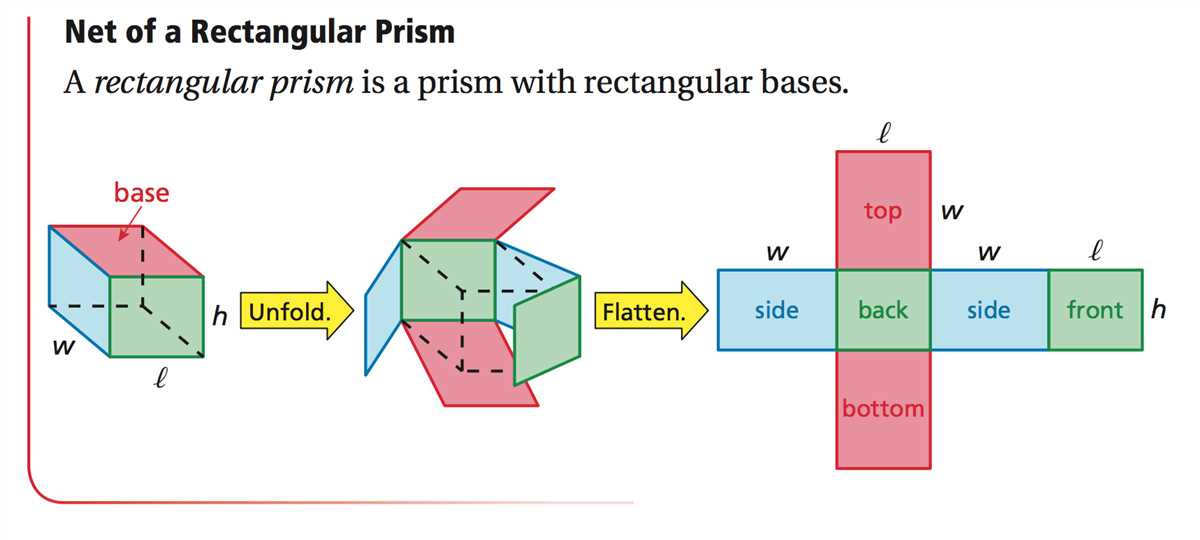
A rectangular prism, also known as a rectangular cuboid, is a three-dimensional shape with six rectangular faces. To calculate its surface area, you need to find the area of each face and add them all together.
Here is a step-by-step guide on how to calculate the surface area of a rectangular prism:
- Identify the dimensions: Start by measuring the length (l), width (w), and height (h) of the rectangular prism. Make sure to use the same units for all measurements.
- Calculate the area of each face: The rectangular prism has six faces – top, bottom, front, back, left, and right. Multiply the length by the width to find the area of the top and bottom faces, and multiply the width by the height to find the areas of the front and back faces. Similarly, multiply the length by the height to find the areas of the left and right faces.
- Find the sum of all face areas: Add up the areas of all six faces to find the total surface area of the rectangular prism.
To demonstrate the calculation, let’s consider a rectangular prism with the following dimensions: length = 6 cm, width = 4 cm, and height = 3 cm.
| Face | Formula | Area |
|---|---|---|
| Top/bottom | l * w | 6 cm * 4 cm = 24 cm² |
| Front/back | w * h | 4 cm * 3 cm = 12 cm² |
| Left/right | l * h | 6 cm * 3 cm = 18 cm² |
To find the total surface area, add up all the face areas: 24 cm² + 24 cm² + 12 cm² + 12 cm² + 18 cm² + 18 cm² = 108 cm².
Therefore, the surface area of the given rectangular prism is 108 cm².
By following these steps, you can accurately calculate the surface area of any rectangular prism, helping you solve a variety of geometry problems and real-life applications.
Common Formulas for Finding Surface Area of Rectangular Prisms
A rectangular prism is a three-dimensional shape that has six faces, each of which is a rectangle. To find the surface area of a rectangular prism, there are several common formulas that can be used.
Formula for finding the surface area of a rectangular prism:
- Surface Area = 2lw + 2lh + 2wh
This formula calculates the sum of the areas of each individual face of the rectangular prism. The first term, 2lw, represents the area of the two larger faces of the prism, which have lengths l and widths w. The second term, 2lh, represents the area of the two side faces, which have lengths l and heights h. The last term, 2wh, represents the area of the top and bottom faces, which have widths w and heights h.
Example:
Let’s say we have a rectangular prism with a length of 5 meters, a width of 3 meters, and a height of 2 meters. We can use the formula to find the surface area:
- Surface Area = 2(5)(3) + 2(5)(2) + 2(3)(2)
- Surface Area = 30 + 20 + 12
- Surface Area = 62
Therefore, the surface area of the rectangular prism is 62 square meters.
Examples of Surface Area Calculations for Rectangular Prisms
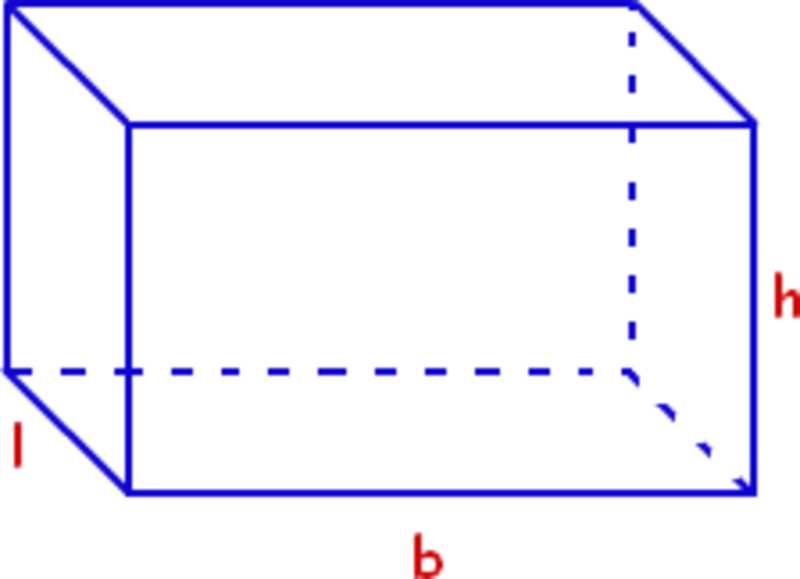
A rectangular prism is a three-dimensional shape with six faces, each of which is a rectangle. To find the surface area of a rectangular prism, you need to calculate the area of each of its faces and then add them together. Here are some examples of surface area calculations for rectangular prisms:
Example 1: Consider a rectangular prism with dimensions of 4 units by 6 units by 3 units. To find the surface area, start by calculating the area of each face. The front and back faces have an area of 4 units by 6 units, which is 24 square units each. The top and bottom faces have an area of 4 units by 3 units, which is 12 square units each. Finally, the left and right faces have an area of 6 units by 3 units, which is 18 square units each. Adding all these areas together, the surface area of the rectangular prism is 2(24) + 2(12) + 2(18) = 48 + 24 + 36 = 108 square units.
Example 2: Let’s take another rectangular prism with dimensions of 10 units by 5 units by 7 units. To find the surface area, calculate the area of each face. The front and back faces have an area of 10 units by 5 units, which is 50 square units each. The top and bottom faces have an area of 10 units by 7 units, which is 70 square units each. The left and right faces have an area of 5 units by 7 units, which is 35 square units each. Adding all these areas together, the surface area of the rectangular prism is 2(50) + 2(70) + 2(35) = 100 + 140 + 70 = 310 square units.
These are just a few examples of how to calculate the surface area of rectangular prisms. Remember to find the area of each face and then add them together to get the total surface area. This calculation is useful in various real-life situations, such as calculating the amount of paint needed to cover the surface of a rectangular box or determining the amount of wrapping paper required to wrap a gift.
Tips and Tricks for Simplifying Surface Area Calculations
Calculating the surface area of a rectangular prism can seem overwhelming at first, but with a few tips and tricks, you can simplify the process and find the answer quickly and efficiently. Here are some key strategies to keep in mind:
1. Break it down into smaller pieces
Don’t try to calculate the surface area of the entire prism all at once. Instead, break it down into smaller rectangular faces and calculate the area of each face separately. Then, add up the areas of all the individual faces to find the total surface area.
2. Use formulas
Remember the formulas for finding the area of a rectangle (length x width) and the area of a square (side length x side length). These formulas can be applied to calculate the surface area of different faces of the rectangular prism. Make sure to use the correct formula for each face.
3. Label the dimensions
Label each side of the rectangular prism with its corresponding length, width, and height. This will help you keep track of the dimensions and avoid confusion when plugging them into the formulas.
4. Use units of measurement
When calculating the surface area, make sure to include the units of measurement in your final answer. This will provide context and ensure that your answer is complete.
5. Double-check your work
After calculating the surface area, take a moment to double-check your work. Make sure you performed all the calculations correctly and that your answer makes sense in the context of the problem. If possible, try to verify your answer using an alternative method or online calculator.
6. Practice, practice, practice
Surface area calculations can be challenging at first, but with practice, they will become easier and more intuitive. Regularly practice solving various surface area problems to sharpen your skills and build confidence in your ability to calculate surface area efficiently.
The Importance of Knowing the Surface Area of Rectangular Prisms in Real-Life Situations
Understanding the concept of surface area for rectangular prisms is not just a mathematical exercise, but an important skill that has practical applications in real-life situations. Whether you realize it or not, surface area calculations are used in various fields and everyday activities.
1. Construction and Architecture:
When designing buildings or structures, architects and engineers need to understand the surface area of rectangular prisms to accurately plan and estimate materials needed. Whether it’s calculating the amount of paint required to cover walls or determining how much flooring is needed, knowledge of surface area allows for more efficient and cost-effective construction.
2. Packaging and Shipping:
Companies involved in packaging and shipping need to calculate the surface area of rectangular prisms to determine the amount of packaging materials required and to optimize the space utilization during transportation. By knowing the surface area, they can minimize packaging costs, reduce wasted space, and ensure the safe delivery of goods.
3. Landscaping and Gardening:
In landscaping and gardening, knowledge of surface area is essential for determining the amount of soil, mulch, or other materials needed to cover a given area. It helps with planning and budgeting, ensuring that there are enough resources to properly nourish and maintain plants and landscapes.
4. Art and Design:
Artists and designers often use rectangular prisms as their canvas or starting point for creative projects. Understanding surface area allows them to accurately measure and visualize the dimensions of their artwork or design, ensuring proportions and balance.
5. Home Improvement:
From painting walls to tiling floors, knowing the surface area of rectangular prisms is crucial in home improvement projects. It helps homeowners determine how much material to purchase, estimate costs, and plan their renovations effectively.
In conclusion, the ability to calculate the surface area of rectangular prisms is not limited to classrooms but has practical significance in various real-life situations. Whether you’re an architect, artist, homeowner, or involved in any field that requires spatial understanding, knowing surface area calculations can help you optimize resources, plan effectively, and make informed decisions.