
If you’re struggling with trigonometry, you’re not alone. Many students find this branch of mathematics challenging, but with the right resources, practice, and guidance, you can conquer it. That’s where the 8 4 trigonometry answer key comes in handy. This comprehensive guide provides answers to the exercises in the 8 4 trigonometry textbook, helping you check your work, understand the concepts better, and ultimately improve your grades.
The 8 4 trigonometry answer key covers a wide range of topics, including angles, right triangles, trigonometric functions, inverse trigonometric functions, and more. Each answer is accompanied by a detailed explanation, breaking down the problem and providing step-by-step solutions. This allows you to not only find the correct answer but also understand the reasoning behind it, reinforcing your understanding of the material.
Whether you’re preparing for a test, completing homework assignments, or simply looking to deepen your knowledge of trigonometry, the 8 4 trigonometry answer key is an invaluable tool. By comparing your answers to the key, you can identify areas where you may need additional practice or review. You can also gain insights into common mistakes and misconceptions, helping you avoid them in the future.
Don’t let trigonometry intimidate you. With the 8 4 trigonometry answer key, you have a valuable resource at your fingertips. Embrace the challenge, use this guide to your advantage, and watch as your confidence and skills in trigonometry soar.
Trigonometry Answer Key: All You Need to Know
Trigonometry is a branch of mathematics that deals with the relationships between the angles and sides of triangles. It plays a crucial role in various fields such as engineering, physics, architecture, and more. To solve trigonometric problems, students often rely on answer keys to check their answers and understand the steps involved in finding the solution.
Trigonometry answer keys provide a comprehensive guide to solving trigonometric equations, identities, and problems. They include step-by-step explanations, formulas, and examples to help students grasp the concepts easily. These answer keys are valuable resources for learners at all levels, whether they are studying trigonometry for the first time or preparing for advanced exams.
Key Components of a Trigonometry Answer Key:
- Formulas and Identities: Trigonometry answer keys provide a list of important formulas and identities that students need to memorize. These include the Pythagorean identities, co-function identities, double angle identities, and more. By referring to these formulas, students can solve trigonometric equations more efficiently.
- Solving Techniques: Answer keys explain the step-by-step solving techniques for various types of trigonometric problems. They cover topics such as finding missing angles and sides, solving triangles, graphing trigonometric functions, and more. Students can follow these techniques to solve similar problems on their own.
- Practice Problems: Answer keys often include a set of practice problems with solutions. These problems help students reinforce their understanding of the concepts and develop their problem-solving skills. By attempting these problems and checking their answers using the answer key, students can identify areas where they need further practice.
Trigonometry answer keys are invaluable tools for students studying trigonometry. They provide clear explanations, formulas, and examples that help students grasp the concepts and solve problems effectively. By utilizing answer keys, students can enhance their understanding of trigonometry and improve their performance in exams and assignments.
Understanding Basic Trigonometric Functions
The study of trigonometry involves understanding and analyzing the relationships between angles and sides in a triangle. Basic trigonometric functions, such as sine, cosine, and tangent, play a fundamental role in this field.
Sine: The sine function is defined as the ratio of the length of the side opposite the given angle to the length of the hypotenuse in a right triangle. It is denoted as sin(theta) or sin(angle). The values of sine range from -1 to 1, and it is a periodic function with a period of 360 degrees or 2π radians.
Cosine: The cosine function is defined as the ratio of the length of the adjacent side to the length of the hypotenuse in a right triangle. It is denoted as cos(theta) or cos(angle). Like the sine function, the values of cosine range from -1 to 1, and it is also a periodic function with a period of 360 degrees or 2π radians.
Tangent: The tangent function is defined as the ratio of the length of the side opposite the given angle to the length of the side adjacent to the angle in a right triangle. It is denoted as tan(theta) or tan(angle). The values of tangent vary from negative infinity to positive infinity, and it is also a periodic function with a period of 180 degrees or π radians.
These basic trigonometric functions can be used to solve various types of problems, such as finding missing sides or angles in a triangle, analyzing periodic phenomena, and modeling real-life situations involving angles and distances. Understanding their properties and relationships is essential for mastering trigonometry and applying it to practical situations.
Solving Trigonometric Equations
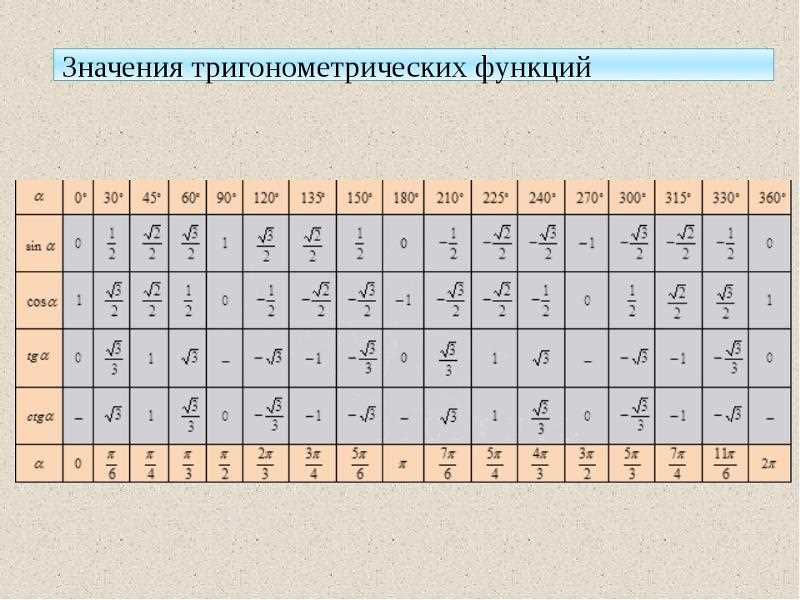
Trigonometric equations involve solving equations that contain trigonometric functions such as sin, cos, and tan. These equations can be challenging to solve, but with the right approach, they can be simplified and solved using various trigonometric identities and properties.
To solve trigonometric equations, it is important to have a good understanding of the basic trigonometric functions and their properties. Additionally, knowledge of trigonometric identities, such as the Pythagorean identity and the double angle formula, can be useful in simplifying the equations and finding their solutions.
One common method of solving trigonometric equations is to isolate the trigonometric function on one side of the equation and use inverse trigonometric functions to find the angle(s) that satisfy the equation. For example, if the equation is sin(x) = 0.5, we can take the inverse sine of both sides to find the angles that have a sine value of 0.5.
In some cases, trigonometric equations may involve multiple trigonometric functions or complex expressions. In such cases, it may be helpful to use algebraic techniques or trigonometric identities to simplify the equation before attempting to find the solutions.
It is important to note that trigonometric equations often have multiple solutions due to the periodic nature of trigonometric functions. When solving these equations, it is important to consider all possible solutions within a given interval.
In conclusion, solving trigonometric equations requires a solid understanding of trigonometric functions, identities, and properties. By using the appropriate techniques and strategies, these equations can be simplified and solved to find the solutions that satisfy the given conditions.
Applications of Trigonometry in Real Life

Trigonometry, the study of relationships and calculations involving angles and lengths, has numerous applications in real life. It has proven to be a valuable tool in various fields like engineering, architecture, physics, and navigation.
In architecture, trigonometry is used to design and construct buildings with precise measurements and angles. Architects use trigonometric equations to calculate the height of structures, determine the angle of roofs, and ensure stability and safety in the construction process.
Trigonometry is also utilized heavily in the field of engineering. It is used to design and analyze structures such as bridges, dams, and towers. Engineers use trigonometric calculations to determine the forces acting on different components of these structures, helping to ensure their stability and longevity.
Another practical application of trigonometry is in navigation. Trigonometric functions are used to determine distances and angles in navigation systems, enabling accurate positioning and route calculations for ships, airplanes, and satellites. Without trigonometry, it would be challenging to accurately navigate and navigate across long distances.
Furthermore, trigonometry plays a significant role in physics and the study of waves and oscillations. Trigonometric functions help describe the motion of waves, determine their amplitudes and frequencies, and analyze their behavior in different physical systems like sound waves, ocean waves, and electromagnetic waves.
In conclusion, trigonometry has numerous practical applications in various fields such as architecture, engineering, navigation, and physics. Its ability to calculate angles, distances, and forces accurately makes it an essential tool in solving real-life problems and improving the efficiency and safety of many processes.
Advanced Trigonometry Concepts
In trigonometry, there are several advanced concepts that build upon the basic principles of the subject. These concepts allow for a deeper understanding of trigonometry and its applications in various fields such as physics, engineering, and geometry. Some of these advanced concepts include:
- Trigonometric Identities: Trigonometric identities are equations that relate different trigonometric functions. They are derived from the fundamental definitions of sine, cosine, and tangent and can be used to simplify trigonometric expressions and solve equations. Some common trigonometric identities include the Pythagorean identities, reciprocal identities, and double angle identities.
- Trigonometric Equations: Trigonometric equations are equations that involve trigonometric functions. These equations often require the use of trigonometric identities to solve. They can be used to find unknown angles or side lengths in triangles or to model periodic phenomena.
- Trigonometric Functions of Angles: Trigonometric functions can also be defined for angles that are not acute. These functions, such as the sine, cosine, and tangent, have specific properties and values for different quadrants on the unit circle. Understanding these functions for angles greater than 90 degrees or negative angles is important for solving trigonometric equations and analyzing periodic functions.
- Inverse Trigonometric Functions: Inverse trigonometric functions are used to find the angle whose trigonometric function value is known. These functions, such as arcsine, arccosine, and arctangent, can be used to solve trigonometric equations and find angles in right triangles.
- Applications of Trigonometry: Trigonometry has numerous applications in fields such as physics, engineering, and geometry. Advanced concepts in trigonometry, such as the law of sines, the law of cosines, and trigonometric functions of angles, are used to solve real-world problems involving triangles, angles, distances, and heights.
By mastering these advanced trigonometry concepts, students can further develop their skills in problem-solving, mathematical reasoning, and analytical thinking. These concepts provide a solid foundation for more advanced mathematics and applications in various disciplines.
Tips for Mastering Trigonometry
Trigonometry can be a challenging subject to master, but with the right techniques and practice, you can become a pro in no time. Here are some tips to help you excel in trigonometry:
- Understand the basics: Before diving into complex trigonometric functions and identities, make sure you have a firm grasp on the basic concepts of sine, cosine, and tangent. Understanding these fundamental trigonometric ratios will form the foundation for your trigonometry knowledge.
- Practice regularly: Trigonometry is a skill that requires practice to truly understand and apply. Set aside dedicated time each day to practice solving trigonometric equations and working through trigonometry problems. The more you practice, the more comfortable you will become with the concepts.
- Review the unit circle: The unit circle is an essential tool in trigonometry. Familiarize yourself with the values of sine and cosine for different angles on the unit circle. Knowing these values will greatly simplify calculations and help you solve trigonometric equations more efficiently.
- Memorize key identities: Trigonometry involves a variety of identities, such as the Pythagorean identities and the reciprocal identities. Take the time to memorize these identities as they will come in handy when simplifying expressions and solving trigonometric equations.
- Seek additional resources: If you’re struggling with a particular concept or finding it difficult to grasp trigonometry as a whole, don’t hesitate to seek additional resources. There are numerous online tutorials, textbooks, and practice exercises available that can provide extra guidance and explanation.
- Break down complex problems: When faced with a complex trigonometry problem, it can be helpful to break it down into smaller, more manageable steps. Identify what information is given, what you are trying to find, and which trigonometric functions or identities can be applied. This approach will make the problem-solving process less overwhelming.
- Ask for help: Don’t hesitate to ask for help if you’re struggling with a concept or problem. Consult your teacher, classmates, or online forums for clarification and guidance. Sometimes, a different perspective or explanation can make all the difference in understanding a difficult trigonometry concept.
By following these tips and dedicating yourself to regular practice, you can master trigonometry and confidently tackle any trigonometry problem that comes your way. Remember, mastery takes time and effort, so be patient with yourself and keep pushing forward. Good luck!
Q&A:
What is trigonometry?
Trigonometry is a branch of mathematics that deals with the relationships between the angles and sides of triangles.
Why is trigonometry important?
Trigonometry is important in various fields, such as physics, engineering, and navigation, as it helps to solve problems involving angles and distances.
How can I study trigonometry effectively?
To study trigonometry effectively, it is important to understand the basic concepts, practice solving problems, and review regularly. Using visual aids and mnemonic techniques can also be helpful.
What are some common trigonometric functions?
Some common trigonometric functions include sine, cosine, and tangent. These functions relate the ratios of the sides of a right triangle to its angles.
Are there any tips for memorizing trigonometric identities?
Yes, some tips for memorizing trigonometric identities include practicing regularly, understanding the derivations of the identities, and using mnemonic devices or visual aids to help remember them.