
In Unit 6, students explore the concept of triangles and congruence. This unit focuses on understanding the properties of triangles, how to prove that two triangles are congruent, and how to apply congruence theorems to solve problems.
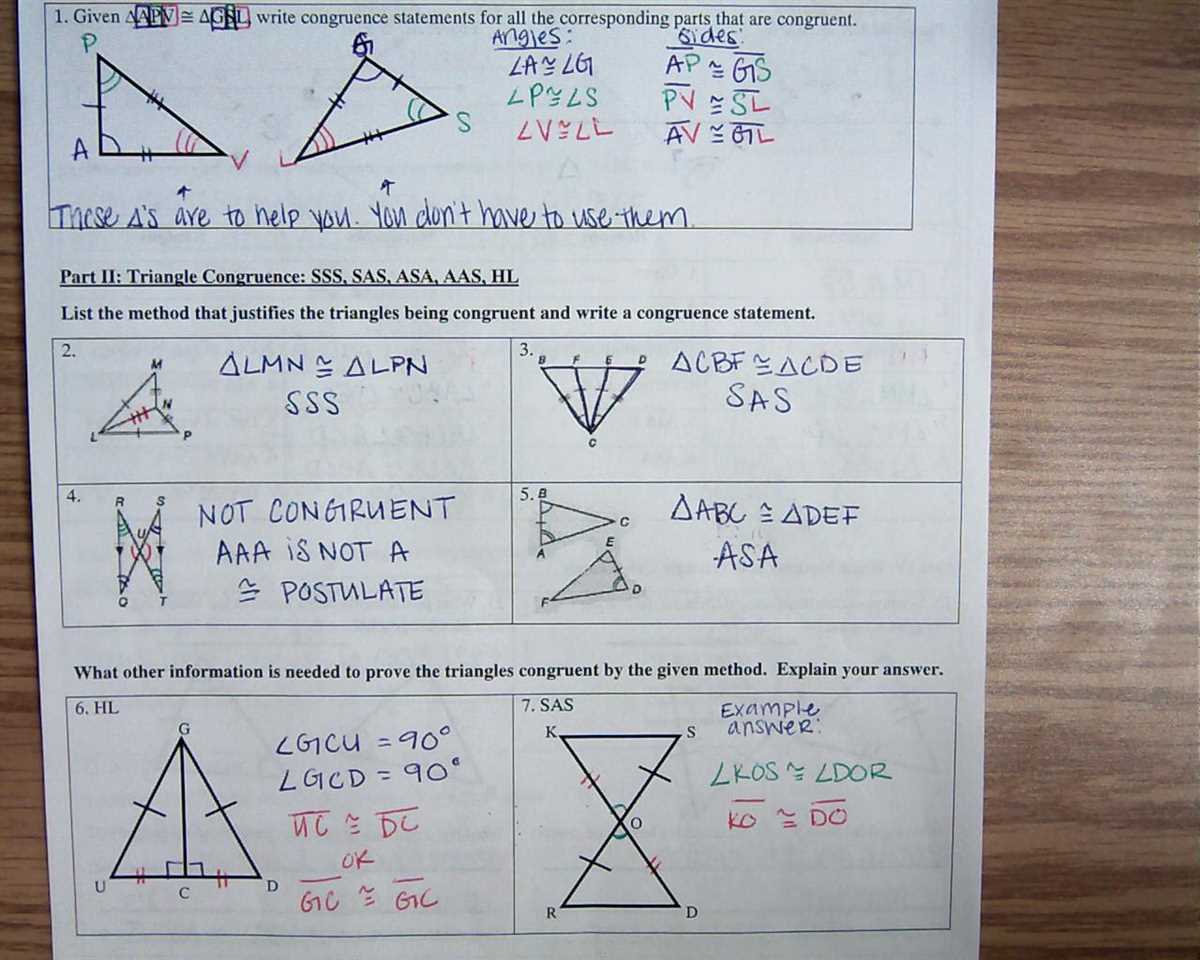
The answer key provided for Unit 6 gives students the opportunity to check their work and review their understanding of the material. It contains step-by-step solutions to all the problems and exercises in the unit to help students identify any mistakes they may have made and to reinforce the concepts and techniques learned.
Through this answer key, students can gain confidence in their ability to solve problems involving triangles and congruence. It allows them to practice their problem-solving skills and verify that they are correctly applying the congruence theorems and postulates discussed in the unit. The answer key serves as a valuable resource for students to assess their progress and to improve their understanding of the material.
Properties of Triangles
Triangles are one of the fundamental shapes in geometry, and they possess several unique properties that distinguish them from other polygons. Understanding these properties is crucial in solving problems and determining the relationships between different triangles.
1. Types of Triangles: Triangles can be classified into different types based on their side lengths and angle measures. There are three main types: equilateral, isosceles, and scalene triangles. Equilateral triangles have all three sides of equal length. Isosceles triangles have two sides of equal length, and scalene triangles have no sides of equal length.
2. Angle Measures: The angles of a triangle always add up to 180 degrees. This property, known as the Triangle Angle Sum Theorem, is a fundamental concept in geometry. Additionally, triangles can be classified based on their angles: acute, right, or obtuse. Acute triangles have all angles less than 90 degrees, right triangles have one angle equal to 90 degrees, and obtuse triangles have one angle greater than 90 degrees.
3. Congruence: When two triangles are congruent, it means that they have the same shape and size. Congruent triangles have corresponding sides and angles that are equal. Congruence is an important concept in geometry and is often used to prove various geometric theorems.
4. Triangle Inequality Theorem: This theorem states that the sum of any two side lengths of a triangle is always greater than the length of the third side. In other words, the longest side of a triangle is always shorter than the sum of the lengths of the other two sides. This theorem helps determine whether a given set of side lengths can form a valid triangle.
5. Pythagorean Theorem: The Pythagorean Theorem is a well-known geometric theorem that relates the sides of a right triangle. It states that the square of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the other two sides. This theorem is widely used in solving problems involving right triangles and is a fundamental concept in trigonometry.
Understanding these properties of triangles is key to solving geometry problems and developing a deeper understanding of the relationships between different triangles. By using these properties, mathematicians and scientists can analyze and solve various real-world problems that involve triangles and their applications in different fields.
Types of Triangles
A triangle is a polygon with three sides and three angles. Triangles can be classified into different types based on their side lengths and angle measurements. Understanding the different types of triangles is important in geometry and can help us solve various mathematical problems.
1. Equilateral Triangle: An equilateral triangle is a triangle that has three equal sides. In other words, all three sides of an equilateral triangle are of the same length. Since all sides are equal, all angles in an equilateral triangle are also equal and measure 60 degrees.
2. Isosceles Triangle: An isosceles triangle is a triangle that has two equal sides. The angles opposite the equal sides are also equal. The third side, called the base, can be of a different length. In an isosceles triangle, the angles opposite the equal sides are called the base angles, and the angle opposite the base is called the vertex angle.
3. Scalene Triangle: A scalene triangle is a triangle that has no equal sides. All three sides of a scalene triangle have different lengths. Since the sides are not equal, the angles of a scalene triangle can also be different.
4. Right Triangle: A right triangle is a triangle that has one 90-degree angle, also known as a right angle. The side opposite the right angle is called the hypotenuse. The other two angles in a right triangle are always acute, meaning they are less than 90 degrees.
5. Obtuse Triangle: An obtuse triangle is a triangle that has one angle greater than 90 degrees. The other two angles in an obtuse triangle are always acute. The side opposite the obtuse angle is the longest side in the triangle, known as the longest base.
Knowing the different types of triangles and their properties can help us determine the congruence of triangles, calculate missing angles or side lengths, and solve various geometric problems.
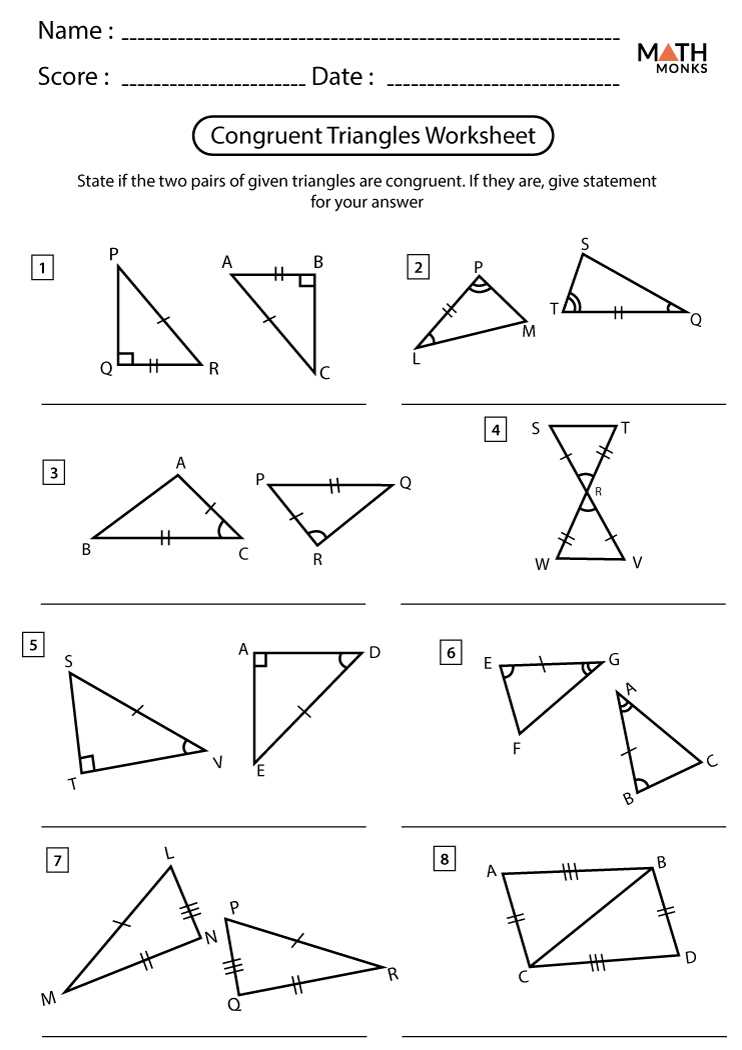
Congruent Triangles
Congruent triangles are triangles that have exactly the same size and shape. In order for two triangles to be congruent, all their corresponding sides and angles must be equal. Congruent triangles can be identified using various methods, including the Side-Side-Side (SSS), Side-Angle-Side (SAS), Angle-Side-Angle (ASA), and Hypotenuse-Leg (HL) criteria.
The Side-Side-Side (SSS) criterion states that if three sides of one triangle are equal in length to three sides of another triangle, then the two triangles are congruent. Similarly, the Side-Angle-Side (SAS) criterion states that if two sides and the included angle of one triangle are equal in length to two sides and the included angle of another triangle, then the two triangles are congruent.
The Angle-Side-Angle (ASA) criterion states that if two angles and the included side of one triangle are equal in measure to two angles and the included side of another triangle, then the two triangles are congruent. Finally, the Hypotenuse-Leg (HL) criterion is specific to right triangles and states that if the hypotenuse and one leg of one right triangle are equal in length to the hypotenuse and one leg of another right triangle, then the two triangles are congruent.
Recognizing congruent triangles is useful in geometry because it allows us to make conclusions about the relationships between their corresponding sides and angles. This can help us solve problems involving triangle congruence, prove geometric theorems, and find unknown measures in triangles.
To summarize, congruent triangles are triangles that have the same size and shape, with all corresponding sides and angles equal. They can be identified using criteria such as SSS, SAS, ASA, and HL. Recognizing congruent triangles is important in geometry as it helps us make deductions and solve various geometric problems.
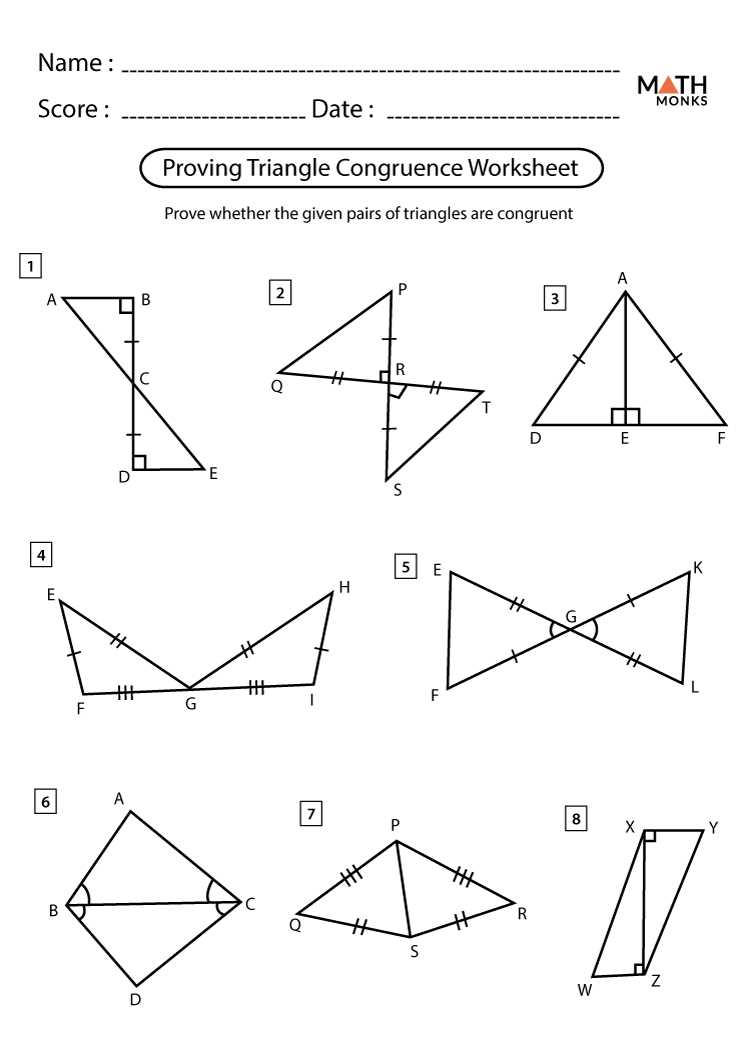
Using Triangle Congruence Theorems
The concept of congruence plays a crucial role in geometry as it allows us to prove that two triangles are identical to each other. Triangle congruence theorems provide a set of guidelines that help determine when two triangles are congruent. These theorems are based on different criteria such as angles, sides, and combinations of both.
One of the most commonly used triangle congruence theorems is the Side-Angle-Side (SAS) theorem. According to this theorem, if two sides and the included angle of one triangle are congruent to the corresponding parts of another triangle, then the two triangles are congruent. This theorem can be used to prove congruence when we have limited information about the triangles.
Another important triangle congruence theorem is the Angle-Side-Angle (ASA) theorem. This theorem states that if two angles and the included side of one triangle are congruent to the corresponding parts of another triangle, then the two triangles are congruent. The ASA theorem is useful when we know the measures of two angles and the length of the included side.
Alongside these theorems, there are also the Hypotenuse-Leg (HL), Side-Side-Side (SSS), and Angle-Angle-Side (AAS) theorems, each with its own set of rules for determining congruence. These theorems are powerful tools in geometry and can be used to solve various problems involving triangles.
In conclusion, triangle congruence theorems provide a systematic way to determine when two triangles are congruent. By analyzing the angles, sides, and combinations of both, we can apply these theorems to find congruent triangles and solve geometry problems. Understanding these theorems and their applications is essential for success in studying and applying geometric principles.
Applying Congruence in Real-Life Situations

Congruence is a fundamental concept in geometry that allows us to determine if two objects are exactly the same size and shape. While it may seem like a purely theoretical concept, congruence is actually quite relevant and applicable in real-life situations.
One of the most common applications of congruence is in the field of construction and engineering. Architects and engineers use congruence to ensure that structures are built accurately and precisely. They rely on congruence to determine if different parts of a building or a bridge are congruent, which helps them ensure structural stability.
Congruence also plays a role in manufacturing and production. Companies that produce goods often use congruence to ensure that their products meet specific size and shape requirements. For example, in the automotive industry, congruence is used to check if different parts of a vehicle, such as doors or windows, are congruent, ensuring proper fit and function.
Furthermore, congruence is relevant in fields such as graphic design and art. Artists and designers often use congruent shapes and patterns to create visually pleasing and balanced compositions. By understanding congruence, they can create harmonious designs that appeal to the viewer’s eye.
In summary, congruence is not just a theoretical concept in geometry, but a practical tool that has a wide range of applications in various industries. From construction to manufacturing to art, congruence helps us ensure accuracy, stability, and visual harmony. Understanding congruence allows us to solve real-life problems and create better, more efficient solutions.