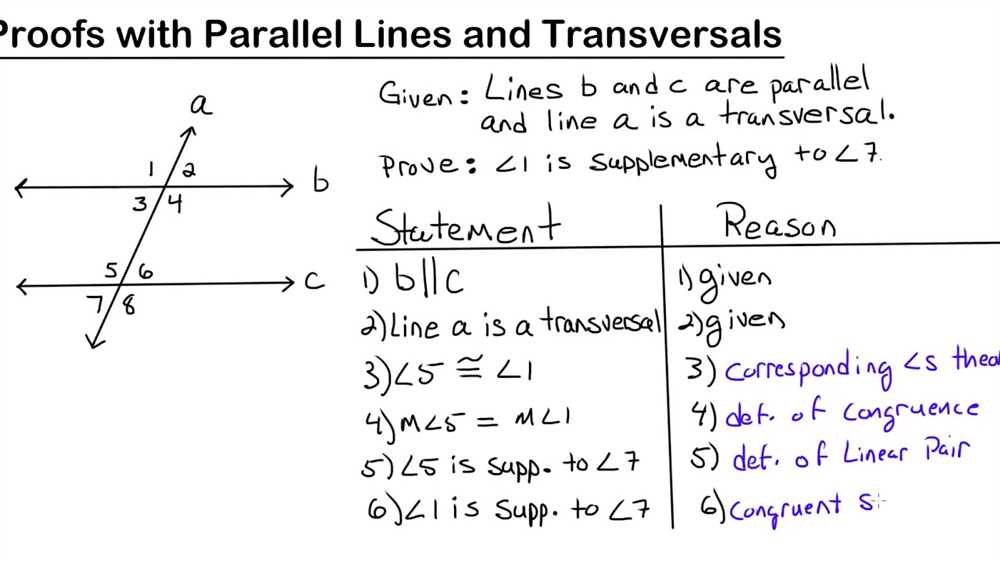
Geometry can seem like a complex subject, especially when it comes to understanding the relationships between parallel lines and transversals. However, with practice and the right answers, you can gain a solid grasp of this fundamental concept. In this article, we will explore the world of parallel lines and transversals, providing you with the tools you need to approach and solve related problems confidently.
Parallel lines are lines that never intersect, no matter how far they are extended. Transversals, on the other hand, are lines that intersect two or more parallel lines. Understanding the angles formed by these lines can help us determine their properties and relationships. By applying the corresponding angles postulate, alternate interior angles theorem, and alternate exterior angles theorem, we can tackle a variety of problems involving parallel lines and transversals.
To hone your skills and deepen your understanding, practice is essential. By answering a range of questions and exercises, you can reinforce your knowledge of parallel lines and transversals. These questions may include identifying pairs of corresponding angles, proving parallel lines based on angle relationships, or finding the measure of a specific angle. By consulting the provided answers, you can check your work and identify any areas that may require further attention. Remember, repetition and practice are key to mastering this topic!
What are parallel lines and transversals in geometry?
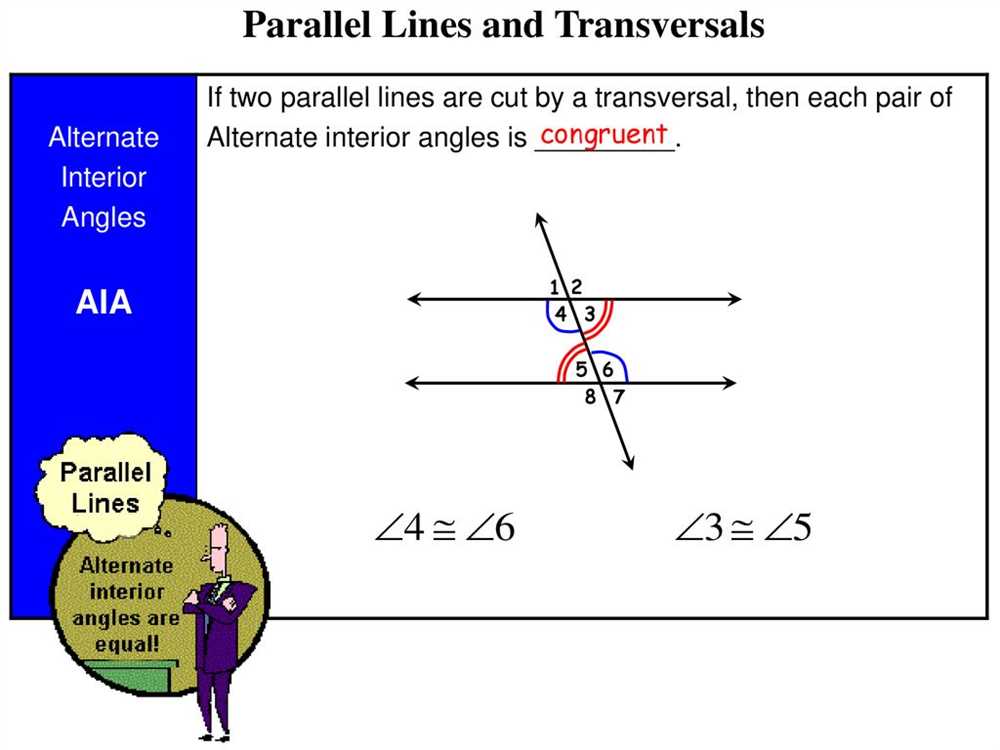
Parallel lines and transversals are important concepts in geometry that describe the relationship between lines and angles.
Parallel lines are two or more lines that are always the same distance apart and never intersect. They can be visualized as railroad tracks, where the two tracks are always parallel to each other. In geometry, parallel lines are denoted by a pair of parallel line symbols (||) placed on top of the lines.
A transversal is a line that intersects two or more other lines. It cuts across the parallel lines and creates various angles. When a transversal intersects two parallel lines, it forms eight angles in total. These angles can be classified into three types: corresponding angles, alternate interior angles, and alternate exterior angles.
Corresponding angles are angles that are in the same position on different lines when intersected by the transversal. They are equal in measure.
Alternate interior angles are angles that are on the opposite sides of the transversal and inside the parallel lines. They are also equal in measure.
Alternate exterior angles are angles that are on the opposite sides of the transversal and outside the parallel lines. They are equal in measure as well.
Understanding parallel lines and transversals is crucial in solving geometric proofs and problems involving angles. They provide a framework for analyzing the relationships between lines and angles in various geometric configurations.
Definition of Parallel Lines
Parallel lines are a fundamental concept in geometry that refers to two straight lines that never intersect. They can be found in various applications of mathematics and play a crucial role in understanding geometric shapes and their properties.
Parallel lines are characterized by two main properties:
- Equal slopes: When two lines are parallel, they have the same slope. Slope is a measure of how steep a line is, and if two lines have the same slope, it means they have the same angle of inclination.
- No intersection: Parallel lines do not meet or intersect each other, no matter how far they are extended. This property implies that the distance between them remains constant along their entire length.
Parallel lines also have important relationships with other geometric elements:
- Transversals: When a third line intersects two parallel lines, it is called a transversal. Transversals form a variety of angles with the parallel lines, such as alternate interior angles, corresponding angles, and consecutive interior angles.
- Parallel planes: In three-dimensional geometry, parallel lines can be extended into parallel planes. Parallel planes are planes that never intersect, and they have the same distance between them at every point.
The concept of parallel lines is widely used in fields such as architecture, engineering, and computer graphics. Understanding their properties and relationships helps in solving geometric problems and analyzing geometric structures with precision and accuracy.
Definition of transversals

In the field of geometry, transversals refer to lines that intersect two or more other lines in a plane. These lines, known as parallel lines, never meet or intersect each other. When a transversal intersects these parallel lines, several angles are formed. Understanding the properties and relationships of these angles is essential in order to solve various geometric problems.
A transversal can form multiple types of angles when it intersects parallel lines. There are three major categories of angles that are formed: corresponding angles, alternate interior angles, and alternate exterior angles.
Corresponding angles are pairs of angles that are located on the same side of the transversal and in the same position relative to the parallel lines. They are equal in measure and have the same angle relationships.
Alternate interior angles are pairs of angles that are located on opposite sides of the transversal and in between the parallel lines. These angles have equal measures and are congruent.
Alternate exterior angles are pairs of angles that are located on opposite sides of the transversal and outside the parallel lines. They are also congruent and have equal measures.
Understanding the properties and relationships of these angles formed by transversals is important in various geometric proofs and applications. It allows mathematicians and students to analyze and solve problems related to parallel lines, such as finding missing angle measures or proving theorems.
Properties of Parallel Lines and Transversals
When dealing with parallel lines and transversals, there are several key properties and relationships that can be observed. These properties provide important insights into the angles formed by parallel lines and the transversals that intersect them.
Corresponding angles: When a transversal intersects two parallel lines, the angles on the same side of the transversal and at the same position relative to the lines are called corresponding angles. Corresponding angles are congruent, meaning they have the same measure.
Alternate interior angles: Alternate interior angles are the angles that are formed on opposite sides of the transversal and inside the two parallel lines. These angles are congruent.
Alternate exterior angles: Alternate exterior angles are the angles that are formed on opposite sides of the transversal and outside the two parallel lines. Like alternate interior angles, these angles are also congruent.
Consecutive interior angles: Consecutive interior angles are the angles that are formed on the same side of the transversal and inside the two parallel lines. These angles add up to 180 degrees and are called supplementary angles.
Parallel lines theorem: If a transversal intersects two parallel lines, then the corresponding angles are congruent, the alternate interior angles are congruent, and the alternate exterior angles are congruent.
By understanding these properties and the relationships between angles formed by parallel lines and transversals, it becomes easier to solve geometric problems and prove theorems in geometry.
Corresponding Angles
In the context of geometry, corresponding angles are pairs of angles that are found in the same relative position at the intersection of two parallel lines and a transversal. These angles are located on the same side of the transversal and in corresponding positions. Corresponding angles have the same relative position and are in congruent locations with respect to the parallel lines.
Corresponding angles can be identified by their location and relationship to the parallel lines. When a transversal intersects two parallel lines, the corresponding angles are formed by the intersection of a pair of corresponding sides on each set of parallel lines. These angles are always congruent, meaning they have the same measure.
For example, if line AB is parallel to line CD, and a transversal intersects these lines at points P and Q, then the angles APQ and CPQ are corresponding angles. Similarly, the angles BDQ and ADQ are also corresponding angles. These corresponding angles are congruent, meaning they have the same measure. In this case, angle APQ is congruent to angle CPQ, and angle BDQ is congruent to angle ADQ.
Corresponding angles play an important role in geometry because they help us prove theorems and solve problems involving parallel lines and transversals. By recognizing and understanding the properties of corresponding angles, we can make deductions and draw conclusions about the relationships between angles and lines in geometric figures.
Alternate Interior Angles
When two parallel lines are intersected by a transversal, several pairs of angles are formed. One important type of angle pair is called alternate interior angles. Alternate interior angles are pairs of angles that are on opposite sides of the transversal and inside the two parallel lines.
The key property of alternate interior angles is that they are congruent, meaning they have the same measure. This property holds true even if the two parallel lines are intersected by multiple transversals. In other words, if two lines are parallel and a transversal intersects them, the alternate interior angles formed by that transversal will always be congruent.
Alternate interior angles are often used in proving theorems and solving geometric problems. They can be used to show that two lines are parallel or to find missing angle measures. By identifying pairs of alternate interior angles in a given diagram, one can determine the relationships between the angles and make deductions based on their congruency.
For example, in the diagram below, lines AB and CD are parallel, and a transversal EF intersects them. Angle 1 and angle 5 are alternate interior angles and are therefore congruent. This fact can be used to prove that lines AB and CD are parallel.
| Angle 1 | Angle 2 | ||
| Angle 5 | Angle 6 | ||
| Line AB | Line CD | ||
| Angle 3 | Angle 4 | ||
| Angle 7 | Angle 8 | ||
Alternate interior angles are an important concept in geometry and have various applications in real-world scenarios, such as analyzing the intersection of roadways or the angles formed by parallel lines in architectural designs. Understanding their properties and relationships can greatly enhance one’s ability to solve geometric problems.
Alternate Exterior Angles
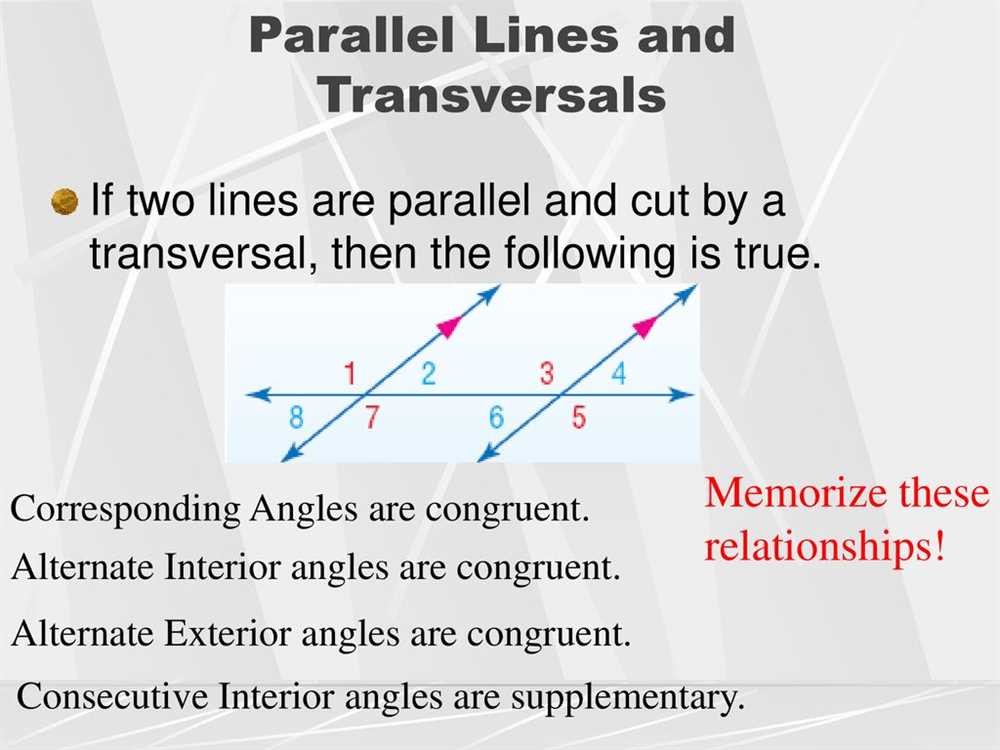
When two parallel lines are intersected by a transversal, several pairs of angles are formed. One such pair is known as alternate exterior angles. Alternate exterior angles are a pair of angles that are on the opposite sides of the transversal and outside the two parallel lines. These angles are equal in measurement.
To identify alternate exterior angles, it is important to remember that the lines being intersected by the transversal are parallel. The transversal then creates two sets of corresponding angles, one on each side of the transversal. The angles that are on opposite sides of the transversal and outside the parallel lines are the alternate exterior angles. These angles can be found at each intersection where the transversal intersects the parallel lines.
For example, if line AB is parallel to line CD and a transversal intersects them, the angles 1 and 8, as well as angles 2 and 7, are alternate exterior angles. Angle 1 is on the opposite side of the transversal from angle 8 and is outside the parallel lines AB and CD. Similarly, angle 2 is on the opposite side of the transversal from angle 7 and is outside the parallel lines. Since the lines are parallel, the measurement of angle 1 is equal to the measurement of angle 8, and the measurement of angle 2 is equal to the measurement of angle 7.
In summary, alternate exterior angles are formed when two parallel lines are intersected by a transversal. These angles are on opposite sides of the transversal and outside the parallel lines. They have equal measurements.
How to Identify Parallel Lines and Transversals

In geometry, parallel lines and transversals play a crucial role in understanding the relationship between different angles and lines. Parallel lines are lines that never intersect, while transversals are lines that intersect two or more parallel lines. By identifying parallel lines and transversals, we can determine various angle relationships and solve geometric problems.
1. Parallel Lines: To identify parallel lines, we look for lines that have the same slope. This means that the lines have the same steepness or inclination. A common way to check if two lines are parallel is by comparing their slopes. If the slopes are equal, the lines are parallel. Another method is to look for pairs of corresponding angles, alternate interior angles, or alternate exterior angles that are equal. If any of these angle pairs are equal, the lines are parallel.
2. Transversals: Transversals are lines that intersect two or more parallel lines. To identify a transversal, we look for a line that intersects two or more other lines at different points. Once we have identified a transversal, we can observe different angle relationships formed by the transversal and the parallel lines. These relationships include corresponding angles, alternate interior angles, alternate exterior angles, consecutive interior angles, and vertical angles. By understanding these angle relationships, we can solve problems involving parallel lines and transversals.
Overall, identifying parallel lines and transversals is important in geometry as it helps us analyze and solve geometric problems. By using slope comparisons and angle relationships, we can determine if lines are parallel or if a line is a transversal. This knowledge allows us to unlock various properties and relationships between angles and lines, enhancing our understanding of geometry concepts.