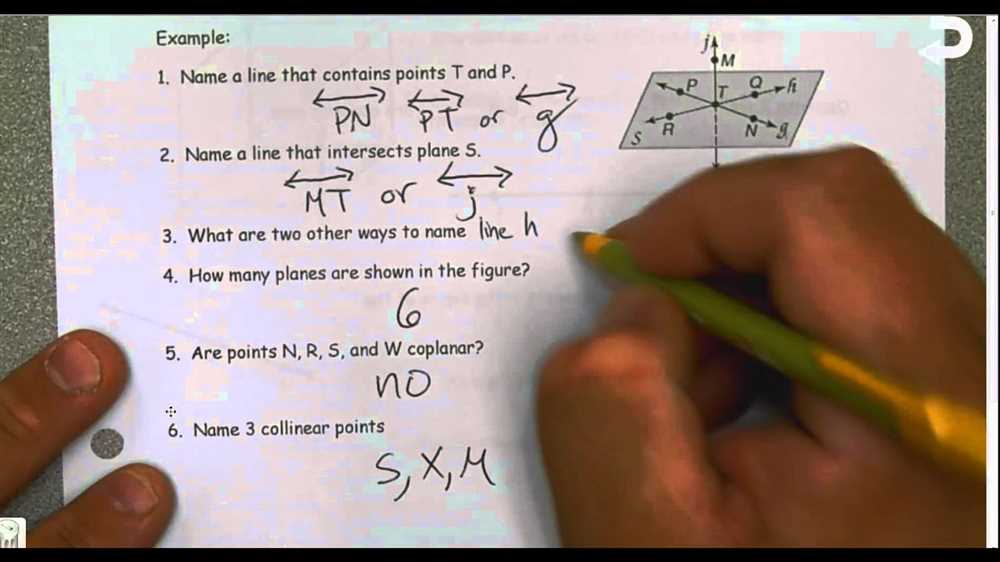
Learning about points, lines, planes, and angles is fundamental in geometry. Understanding these concepts allows us to describe and analyze the relationships and properties of geometric figures. In this article, we will provide the answer key for the homework exercises related to points, lines, planes, and angles.
Firstly, let’s review the basic definitions. A point is a location in space that has no size or dimension. It is represented by a dot. A line is a straight path that extends infinitely in both directions. It is made up of points and has no thickness. A plane is a flat surface that extends infinitely in all directions. It is made up of lines and has no thickness. Lastly, an angle is formed by two rays with a common endpoint.
Now let’s look at some examples of homework exercises related to these concepts. Exercise 1 asks to identify the name of three points in a given diagram. The correct answer would be to identify the points as “A,” “B,” and “C.” Exercise 2 asks to name the line that contains points “D,” “E,” and “F.” The correct answer would be to name it as line “DE.” Exercise 3 asks to identify the plane that contains lines “GH” and “IJ.” The correct answer would be to identify the plane as plane “GIJH.”
In addition to identifying points, lines, and planes, we also need to understand angles. Exercise 4 asks to classify an angle based on its measurement. If the angle measures 90 degrees, the correct answer would be to classify it as a “right angle.” Exercise 5 asks to identify two angles that are complementary. The correct answer would be to identify angles that add up to 90 degrees.
In conclusion, understanding the concepts of points, lines, planes, and angles is crucial in geometry. These concepts help us describe and analyze geometric figures. The answer key provided for the homework exercises related to points, lines, planes, and angles will assist students in practicing and reinforcing these concepts.
Section 2: Understanding Points and Their Characteristics
In this section, we will explore the concept of points and their characteristics in geometry. A point is a fundamental building block in geometry, representing a specific location in space. It has no size, shape, or dimension, but it is the foundation upon which other geometric objects are constructed.
Properties of Points: Points have several characteristics that define and distinguish them. Firstly, points are unique and distinct. Each point in space is different from any other point, allowing us to identify and refer to specific locations. Additionally, points have no length, width, or height. They are infinitesimally small and cannot be measured. Points also have no orientation. They can be freely moved, rotated, or reflected without changing their identity.
Naming Points: Points are typically named using capital letters, such as A, B, C, and so on. This naming convention allows us to refer to specific points when discussing geometric figures and relationships. Sometimes, points are labeled based on their location in relation to other objects. For example, a point on a line can be labeled as a lowercase letter, followed by a prime symbol (e.g., A’), to indicate its position along the line.
Location of Points: Points can exist in various positions within a given space. They can be located on a line, within a plane, or in three-dimensional space. When discussing the relationship between points, we often use terms like collinear (lying on the same line), coplanar (lying on the same plane), or non-collinear (not lying on the same line).
Distance between Points: In geometry, the distance between two points is a measure of the straight-line length between them. It is calculated using the distance formula, which takes into account the coordinates or positions of the points in space. Understanding the concept of distance is essential for determining the length of line segments and the relationships between points.
In summary, points are the basic building blocks of geometry, representing specific locations in space. They have unique characteristics, including their lack of size, shape, and orientation. By studying the properties and relationships of points, we can better understand the geometry of lines, planes, and angles.
Section 3: Exploring Lines and Their Properties

In Section 3, we will delve deeper into the study of lines and explore their various properties. A line is a straight one-dimensional figure that extends infinitely in both directions. It has no thickness and is composed of an infinite number of points. In this section, we will learn about different types of lines and their characteristics.
One key concept we will investigate is the different ways lines can intersect. When two lines intersect, they form angles. These angles can be categorized into different types based on their properties. For example, when two lines intersect and the angles opposite each other are equal, the lines are said to be perpendicular. Perpendicular lines form a right angle, which measures 90 degrees.
- Parallel lines are another important type of line. Parallel lines are lines that never intersect, no matter how far they are extended. They can be visualized as train tracks that run alongside each other in the same direction but never cross. Parallel lines have the same slope and do not share any common points.
- Another interesting property of lines is their inclination. The inclination of a line refers to its steepness or slope. A line can have a positive, negative, zero, or undefined slope. A positive slope indicates an upward inclination, while a negative slope indicates a downward inclination. A zero slope represents a horizontal line, while an undefined slope represents a vertical line.
- We will also explore the concept of transversals, which are lines that intersect two or more parallel lines. Transversals create a variety of angles, such as alternate interior angles, corresponding angles, and consecutive interior angles. These angles have unique properties and relationships that we will examine in this section.
By studying lines and their properties, we can better understand the fundamental building blocks of geometry and apply this knowledge to solve a variety of mathematical problems. In the next few lessons, we will delve further into the intricacies of lines, angles, and their relationships.
Section 4: Analyzing Planes and Their Attributes

In this section, we will focus on analyzing planes and their attributes. A plane is a flat, two-dimensional surface that extends infinitely in all directions. It is defined by at least three non-collinear points or a line and a point not on that line.
Attributes of a Plane:
- Normal Vector: A plane can be represented by a normal vector, which is a vector perpendicular to the plane. The normal vector helps determine the orientation of the plane.
- Equation of a Plane: The equation of a plane helps describe its position in space. It is typically represented in the form Ax + By + Cz = D, where A, B, C, and D are constants.
- Intercepts: The intercepts of a plane are the points at which it intersects the x-, y-, and z-axis. They can provide valuable information about the position of the plane in space.
- Parallel and Perpendicular Lines: Planes can be parallel to each other, meaning they never intersect, or perpendicular, meaning they intersect at a right angle.
Analyzing Planes:
When analyzing planes, it is important to consider their orientation, position, and relationship to other objects in space. Calculating the normal vector and determining the equation of a plane can help provide a clear understanding of its attributes. Additionally, examining the intercepts of a plane and its relationship to parallel or perpendicular lines can further enhance our analysis. Understanding these concepts will allow us to solve problems involving planes more effectively and accurately.
Section 5: Investigating Angles and Their Types
In this section, we will delve deeper into the study of angles and explore their different types. Angles are fundamental geometric elements that are formed by two rays with a common endpoint called the vertex. They are measured in degrees and provide us with a way to quantify the amount of rotation or turning between two lines or planes.
Angle Classification:
- Acute Angle: An acute angle is an angle that measures less than 90 degrees. In other words, the two rays forming the angle are closer together, resulting in a smaller degree of rotation.
- Right Angle: A right angle is exactly 90 degrees. It forms a perfect corner and is often seen in squares and rectangles.
- Obtuse Angle: An obtuse angle measures greater than 90 degrees but less than 180 degrees. The two rays forming the angle are further apart, resulting in a larger degree of rotation.
- Straight Angle: A straight angle measures exactly 180 degrees. It forms a straight line and is often seen in vertical and horizontal lines.
- Reflex Angle: A reflex angle measures greater than 180 degrees but less than 360 degrees. It is often seen in shapes with more than two sides, such as polygons.
Understanding the different types of angles and their properties is important when working with geometric shapes, as angles play a crucial role in determining the relationships between lines and planes. By investigating angles and their types, we can gain a deeper understanding of the principles of geometry and how they apply to real-world situations.
Section 6: Solving Homework Problems on Points, Lines, Planes, and Angles

In this section, we will explore various strategies for solving homework problems on points, lines, planes, and angles. These concepts are fundamental to geometry and play a crucial role in understanding the relationships between different geometric objects.
To solve homework problems on points, lines, planes, and angles, it is essential to have a clear understanding of the definitions and properties associated with these concepts. For example, understanding the characteristics of collinear and non-collinear points, intersecting and parallel lines, coplanar and non-coplanar planes, and complementary and supplementary angles will be crucial for solving problems effectively.
One strategy for solving homework problems on points, lines, planes, and angles is to carefully read the problem statement and identify the relevant information. It is important to identify the given quantities, such as the coordinates of points or the measures of angles, and any additional information provided, such as the relationships between different points or angles.
Another strategy is to visualize the problem by drawing a diagram or sketch. This can help to clarify the relationships between different geometric objects and make it easier to identify potential strategies for solving the problem. It is important to label the different points, lines, planes, and angles in the diagram to keep track of the given information.
Once the relevant information has been identified and a diagram has been drawn, the next step is to apply the appropriate formulas or theorems to solve the homework problem. This may involve using properties of parallel lines, angles formed by transversals, the Pythagorean theorem, or other geometric concepts. It is important to carefully apply the formulas or theorems and show all necessary steps to ensure a correct solution.
Finally, it is important to check the solution to ensure its accuracy. This can be done by verifying that the solution satisfies all the conditions stated in the problem and by checking the calculations for errors. If the solution does not meet the stated conditions or if there are errors in the calculations, it may be necessary to revise the solution and recheck the steps.
In conclusion, solving homework problems on points, lines, planes, and angles requires a clear understanding of the concepts, careful reading of the problem statement, visualization of the problem through diagrams, application of appropriate formulas or theorems, and thorough checking of the solution. By following these strategies, students can effectively solve homework problems and deepen their understanding of geometry.
Section 7: Answer Key for Homework Questions

Here is the answer key for the homework questions in Section 7. Please refer to it to check your answers and ensure you understand the concepts.
- Question 1: Find the midpoint of the line segment with endpoints A(2, 4) and B(6, 8).
- Answer 1: The midpoint is calculated by taking the average of the x-coordinates and the average of the y-coordinates. So, the midpoint is M(4, 6).
- Question 2: Determine the distance between the points C(3, 5) and D(9, 2).
- Answer 2: The distance between two points is calculated using the distance formula: sqrt((x2 – x1)^2 + (y2 – y1)^2). Plugging in the values, we get sqrt((9 – 3)^2 + (2 – 5)^2) = sqrt(36 + 9) = sqrt(45) = 3 * sqrt(5).
- Question 3: Find the equation of the line that passes through the point E(4, -2) and has a slope of 2.
- Answer 3: The equation of a line can be written in the form y = mx + b, where m is the slope and b is the y-intercept. Plugging in the values, we get y = 2x + b. To find the value of b, we can substitute the coordinates of the point E into the equation. -2 = 2 * 4 + b, which simplifies to -2 = 8 + b. Solving for b, we get b = -10. So, the equation of the line is y = 2x – 10.
Make sure to check your answers and review any concepts you may not fully understand. This section is crucial for understanding the basics of points, lines, planes, and angles.